PBR中的辐射度量学

PBR的核心法则是基于物理，在渲染领域最关注的就是光，更具体而言是光的表现以及光和物体的交互。而光也是一种电磁辐射，因此渲染中最主要的理论依据都源自辐射度量学(radiometry)，这是专门研究电磁辐射量化的学科。

Domains and measures

在量化电磁辐射之前，需要对场景有一个定义。首先将场景几何抽象为 \(\mathcal{R}^3\)​​​ 中的面(surfaces)的有限集 \(\mathcal{M}\) ，这里的表面是指分段可微的二维流形(Manifold)，出于实现考虑，这里的流形默认都是存在边界 \(\partial \mathcal{M}\) 的，否则邻接面之间可能会存在缝隙(gaps)。而 \(\mathcal{M}\)​​ 作为一个集合，其本身并不一定是流形，如：仅含两个相切球的场景。

这些表面会把整个空间划分为一个个相连的区域，而为了简化模型，这里先不考虑体吸收(volume absorption)、自发光(emission)、散射(scattering)等情况，即假设每个区域中都只有非参与介质，这些介质被抽象描述为一个固定的折射率。当然，表面也不一定充当区域划分的边界，如：一个悬浮的平台。

对于一个域 \(D\subset\mathcal{M}\)​ ，定义度量 \(A(D)\)​​ 表示该域的面积，则勒贝格(Lebesgue)积分为

\[\int_\mathcal{M}f(x)\ dA(x) \]

其中， \(f:\mathcal{M}\rightarrow \mathcal{R}\)​ 是关于表面积的函数。

而方向可以被定义为一个单位向量 \(\omega\in \mathcal{R}^3\) ，所有方向构成一个集合 \(\mathcal{S}^2\) ，显然这是空间中的单位球面。设 \(\sigma\) 表示 \(\mathcal{S}^2\) 上的面积度量，则对于给定的方向集合 \(D\in \mathcal{S}^2\) ，可以定义其对应的立体角(solid angle)为 \(\sigma(D)\) 。类似地，对于一个表面 \(P\) ，将其上的点投影到以点 \(x\) 为球心的单位球面上，这些点所代表的方向的集合的度量，即为 \(P\) 在点 \(x\) 处所对的(subtend，类似平面几何中线段相对于点的对角)立体角。从定义可以看出，立体角本质上是一种面积度量，可以理解为：我们站在某点观测某一物体，物体表面上的每一点都对应着一个观测方向，这些观测方向单位化后的集合也就是对应的立体角。由此，我们可以把通量等描述在由方向构成的立体角上，这么做有利于简化之后对光的各种物理量的描述。

由此派生的一个概念就是投影立体角(projected solid angle)，这一概念通常用于描述irradiance。对于给定点 \(x\) ， \(N(x)\) 表示表面法线，给定一个方向集合 \(D\subset \mathcal{S}^2\) ，投影立体角 \(\sigma_x^\perp\) 定义为

\[\sigma_x^\perp(D)=\int_D|\omega\cdot N(x)|\ d\sigma(\omega) \]

其中，点积通常也被写为 \(\cos\theta\) ，这里的 \(\theta\) 是指 \(\omega\) 的极角，即 \(\omega\)​ 与法线的夹角。

其名称源于最初定义时使用了投影这一操作。设 \(T_M(x)\) 为点 \(x\) 的切空间，即由垂直于法线的向量构成的空间

\[T_M(x)=\{y\in \mathcal{R}^3|y\cdot N(x)=0 \} \]

注意：这里所定义的切空间包含了原点，即这是一个线性空间，而非仿射空间。整个切空间将 \(\mathcal{S}^2\) 分为了两个半球，分别为上半球：

\[\mathcal{H}_+^2(x)=\{\omega\in \mathcal{S}^2|\omega\cdot N(x)>0\} \]

和下半球：

\[\mathcal{H}_-^2(x)=\{\omega\in \mathcal{S}^2|\omega\cdot N(x)<0\} \]

对于任一半球上一个给定的方向集合 \(D\)​​ ，其投影立体角就是该集合正交投影到切空间后的面积度量。一个最简单的例子：对于一点处的整个上半球表面，其对应的投影立体角就是整个单位圆，故

\[\sigma_x^\perp(\mathcal{H}_+^2)=\pi \]

The phase space

普遍的transport理论研究的是抽象环境中的粒子运动，由于光的粒子性，基于该理论可以定义一系列和辐射相关的物理量。

我们可以用若干时变参数(参数是时间的函数)描述一个粒子。最基本地，可以用位置和速度两个参数描述一个粒子，其包含6个自由度。由此，可以用一个 \(6N\) 维向量描述一个包含 \(N\) 个粒子的系统。而我们可以将系统状态视为一个在 \(6N\)​ 维相空间(phase space)中的点，这个空间包含了所有可能的系统状态。系统状态随时间的改变，在相空间上反映为一条一维曲线。

假设光不发生偏振和干涉，则每个光子可由位置 \(x\) ，运动方向 \(\omega\) ，波长 \(\lambda\) 描述。若方向用立体角描述，此模型下，整个相空间也是 \(6N\)​​ 维。对于不发生相互作用的粒子(如：光子)，保留这么高维度的相空间意义不大，此时可以让相空间维度对应于单个粒子的状态。基于这个约定，相空间 \(\psi\) 可以降至 \(6\) 维，且可表示为

\[\psi=\mathcal{R}^3\times \mathcal{S}^2\times \mathcal{R}^+ \]

此时可以用该空间中的 \(N\)​​ 个点表示整个系统的状态，每个点的位置(六个维度的坐标)均为时变参数。

辐射度量学中涉及的物理量都可以在相空间中给出度量，度量值可以经简单计算给定区域中光子的数量而得出，也可以由一或多个参数的density导出定义。如最基本的，光子数量 \(N_P\)​ 就是相空间中给定域内的光子数量的度量。

The trajectory space and photon events

在相空间的基础上显式引入时间维度，考虑将相空间中的所有光子随时间的变化以图的方式描述出来，我们可以得到一组一维曲线，并称这组曲线所在的空间为轨迹空间(trajectory space)

\[\Psi=\mathcal{R}\times\psi \]

辐射的各种度量就定义在这些曲线上，沿这些曲线指定一组光子事件(photon events)，然后通过多种方式测量事件的分布，即可定义一个度量。

事件：在物理学中，是指时空间和相空间所指定的时空中的一点，即轨迹空间中的一点。

通过指定一个时间面得到该面与光子轨迹的交点，即可定义一个光子事件。如：选取一个时间 \(t_0\) ，在轨迹空间中，超平面 \(t=t_0\) 与光子轨迹的交点就是该时刻的光子状态，即光子事件。同样，对于给定的 \(\mathcal{R}^3\) 中的平面 \(P\) ，可以定义光子事件为 \(P\) 在轨迹空间中与超平面 \(\mathcal{R}\times P\times \mathcal{S}^2\times \mathcal{R}^+\) 的交集。

一个合理的假设是，轨迹空间包含着数量庞大的事件，因此，事件的密度可以采用连续分布进行建模。也就是说，虽然实际上一个光子的能量是固定的，能量的分布是离散的，但我们可以假设其可以是任意非负实数，能量的取值是连续的。

Radiometric quantities

辐射的度量总是围绕几个重要的物理量展开，而以下的定义是经过简化的，并非完全严格的公理化定义。

Power

Radiant flux (power) is the energy emitted reflected, transmitted or received, per unit time.

辐射量(radiant power)是指单位时间内的能量(energy)

\[\Phi={dQ\over dt} \]

其量纲为瓦特 \(\mathrm{watts[W=J\cdot s^{-1}]}\)​​ ，描述的是有限表面 \(S\subset \mathcal{R}^3\)​​ 发出或吸收的能量的速率。

通常并不会直接定义 \(Q\) ，而是定义轨迹空间中的某个区域 \(D(t)\) ，该区域随时间变化，而区域内的光子能量即为 \(Q(t)\)​ 。例如：考虑度量区域

\[D(t)=[0,t]\times \mathcal{S}\times \mathcal{S}^2\times \mathcal{R}^+ \]

中发出的能量，其中， $ S\subset \mathcal{R}^3$ 为有限表面，则 \(Q(t)\) 表示 \(S\) 在时间 \([0,t]\) 所发出的能量，故

\[\Phi(t)={dQ(t)\over dt} \]

表示的就是单位时间发出的能量。这也是更为直观的形式。但通常我们只关注系统达到稳态时的能量分布，此时相空间并不随时间改变，可忽略参数 \(t\) ，回到定义的形式。

Irradiance

The irradiance is the power per (perpendicular / projected) unit area incident on a surface point.

辐照度(irradiance)是指单位面积的辐射量

\[E(x)={d\Phi(x)\over dA(x)} \]

其量纲为 \([W\cdot m^{-2}]\) 。其定义总是依赖于点 \(x\) 以及给定的法线 \(N(x)\)​ 所确定的平面，而ir词缀其实也暗示着其通常用于描述接收的辐射，且通常是在一个面上的辐射，即来自指定的半球。

Radiance

The radiance (luminance) is the power emitted, reflected, transmitted or received by a surface, per unit solid angle, per projected unit area.

辐射(radiance)描述的是点 \(x\) 处，对于给定方向 \(\omega\) ，在微分立体角 \(d\sigma(\omega)\) 内，通过微表面 \(dA_\omega^\perp(x)\) 的能量

\[L(x,\omega)={d^2\Phi(x,\omega)\over dA_\omega^\perp(x)\ d\sigma(\omega)} \]

其中， \(A_\omega^\perp\)​ 是垂直于 \(\omega\)​​ 的一个假想平面。其量纲为 \([W\cdot m^{-2}\cdot sr^{-1}]\)​ ，其中， \(sr\)​​​ 是立体角的量纲steradian。在定义中，接收平面是必须垂直于给定方向的，即考量的总是投影面积。

而当度量的是一个实际的平面 \(S\) 上的radiance时，公式可以更直观地表示为

\[L(x,\omega)={d^2\Phi(x,\omega)\over|\omega\cdot N(x)|\ dA(x)\ d\sigma(\omega)} \]

其中， \(A\) 是 \(S\) 的面积， \(N(x)\) 是表面法线，上式实际上包含了求投影的运算，因为

\[dA_\omega^\perp(x)=|\omega\cdot N(x)|\ dA(x) \]

而根据投影立体角的定义， \(\cos\) 项可以与微分立体角组合构成微分投影立体角，则有

\[L(x,\omega)={d^2\Phi(x,\omega)\over dA(x)\ d\sigma_x^\perp(\omega)} \]

这也是最常使用的式子，因为这里参与运算的是 \(S\) 的实际面积 \(A\) 。

Spectral radiance

将波长纳入考虑即可进一步定义光谱辐射(spectral radiance)

\[L_\lambda={dL\over d\lambda} \]

即

\[L_\lambda(x,\omega,\lambda)={d^3\Phi(x,\omega)\over dA(x)\ d\sigma_x^\perp(\omega)\ d\lambda} \]

其量纲为 \([W\cdot m^{-2}\cdot sr^{-1}\cdot nm^{-1}]\)​ 。同理可定义spectral power等。光谱辐射通常作为最基本的物理量，其他量都可以由其推出，如对波长积分可以得到radiance，对投影角积分可以得到irradiance。

Incident and exitant radiance functions

通常我们研究的函数采用如下形式

\[L:\mathcal{M}\times \mathcal{S}^2\rightarrow \mathcal{R} \]

即radiance表示为场景中的面和立体角构成的相空间到一维空间的映射，等价于

\[L:R^3\times \mathcal{S}^2\rightarrow \mathcal{R} \]

虽然物理上，radiance不能为负，但为了保证空间的线性性，我们仍保留其中的负数部分。根据 \(\omega\)​ 的不同，我们把radiance分为incident(入射) radiance和exitant(出射) radiance。incident radiance \(L_i(x,\omega)\)​ 描述的是从 \(\omega\)​ 方向到达 \(x\)​ 点的radiance，exitant radiance \(L_o(x,\omega)\)​ 描述的是在 \(x\)​ 点沿 \(\omega\)​​ 方向发出的radiance，显然有

\[L_i(x,\omega)=L_o(x,-\omega) \]

但实际上，划分为这两类是因为其具有本质区别，前者表示的是光子到达表面前的状态，后者表示的是光子离开表面后的状态。

The bidirectional scattering distribution function

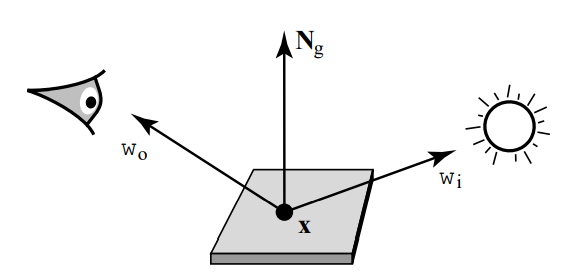
双向散射分布函数(bidirectional scattering distribution function，BSDF)是对表面光线散射性质的数学描述。设场景中某表面上一固定点为 \(x\in\mathcal{M}\) ，考察在方向 \(\omega_o\) 上从 \(x\) 发出的radiance \(L_o(\omega_o)\) ，这里暂时忽略位置 \(x\) ，显然 \(L_o(\omega_o)\) 的值取决于在所有方向上总共有多少radiance到达了 \(x\) 。首先分析来自某个特定的入射方向的贡献，考虑入射方向 \(\omega_i\) ，以 \(\omega_i\) 为轴构建一个极小椎体，这个椎体可以描述为一个微分立体角 \(d\sigma(\omega_i)\)​ ，来自该椎体的入射光击中表面上的点 \(x\) 并产生irradiance \(dE(\omega_i)\)​

\[dE(\omega_i)=L_i(\omega_i)\ d\sigma^\perp(\omega_i) \]

随后这部分光线会被表面散射到各个方向，设沿方向 \(\omega_o\) 散射的radiance为 \(dL_o(\omega_o)\) ，由于一般情况下光都是可简单叠加的，即满足线性性，因此无论 \(dE(\omega_i)\) 的变化是来自 \(L_i\) 还是 \(d\sigma(\omega_i)\)​ ，都有

\[dL_o(\omega_o)\propto dE(\omega_i) \]

而BSDF \(f_s(\omega_i\rightarrow\omega_o)\) 描述的正是这个比例常数，即

\[f_s(\omega_i\rightarrow\omega_o)={dL_o(\omega_o)\over dE(\omega_i)}={dL_o(\omega_o)\over L_i(\omega_i)\ d\sigma^\perp(\omega_i)} \]

用自然语言描述上式： \(f_s(\omega_i\rightarrow\omega_o)\) 表示来自 \(\omega_i\) 的每一单位irradiance会有多少比例被转化为 \(\omega_o\) 方向上出射的radiance， \(\omega_i\rightarrow\omega_o\) 形象描述光的传播方向。

The scattering equation

根据BSDF的定义，我们可以把differential exitant radiance表示为

\[dL_o(\omega_o)=L_i(\omega_i)f_s(\omega_i\rightarrow\omega_o)\ d\sigma^\perp(\omega_i) \]

此时只要对来自所有方向的irradiance对radiance的贡献求积分，就可以得到 \(\omega_o\)​ 方向上的exitant radiance了，即

\[L_o(\omega_o)=\int_{S^2}L_i(\omega_i)f_s(\omega_i\rightarrow\omega_o)\ d\sigma^\perp(\omega_i) \]

这就是(表面)散射方程(scattering equation)。

在有了散射方程之后，对于给定的入射光照，我们可以计算出表面任一点的radiance，基于几何光学对光的唯象表达，这个方程实际上就给出了物体表面外观(即材质)的一个数学表示(尽管它并不能描述所有的光学现象或材质表现)。

The BRDF and BTDF

BSDF并非辐射度量学中的标准概念。通常，散射光会被拆分为反射光(reflected)和透射光(transmitted)两部分，由此也就有了双向反射分布函数(bidirectional reflectance distribution function，BRDF) \(f_r\) 和双向透射分布函数(bidirectional transmittance distribution function，BTDF) \(f_t\) 。

通过限制域即可得到

\[f_r:\mathcal{H}_i^2\times\mathcal{H}_r^2\rightarrow\mathcal{R} \]

其中， \(\mathcal{H}_i^2\) 和 \(\mathcal{H}_r^2\) 分别为入射半球和反射半球，但其实两者表示的是同一个方向集合(上半球 \(\mathcal{H}_+^2\) 或下半球 \(\mathcal{H}_-^2\)​ )。

同理有

\[f_t:\mathcal{H}_i^2\times\mathcal{H}_t^2\rightarrow\mathcal{R} \]

其中， \(\mathcal{H}_i^2=-\mathcal{H}_t^2\) ，即两者互补(同样，两者可分别为上半球 \(\mathcal{H}_+^2\) 和下半球 \(\mathcal{H}_-^2\) ，或相反)。

因此，BSDF其实是由两个BRDF和两个BTDF组成的(在两个半球上都各自需要一个BRDF和一个BSDF)。

由于BRDF描述的是实际表面上的性质，其具有一些天然的性质，其中最主要的是对称性(symmetric)和能量守恒(energy conservation)。

对称性即

\[f_r(\omega_i\rightarrow\omega_o)=f_r(\omega_o\rightarrow\omega_i),\forall\omega_i,\omega_o \]

能量守恒即

\[\int_{\mathcal{H}_o^2}f_r(\omega_i\rightarrow\omega_o)\ d\sigma^\perp(\omega_o)\le1,\forall\omega_i\in\mathcal{H}_i^2 \]

Angular parameterizations of the BSDF

采用单位向量描述的立体角在计算上并不方便，因此需要对角度进行参数化。对于 \(\omega\in \mathcal{S}^2\) ，其可以表示为一组角向量 \((\theta,\phi)\) ，其中极角(polar angle) \(\theta\) 是指 \(\omega\) 和法线 \(N\) 的夹角，方位角(azimuthal angle) \(\phi\) 是指在切空间内 \(\omega\) 与 \(x\) 处的一个特定方向 \(T\) 的夹角，即有

\[\begin{aligned} \cos\theta=\omega\cdot N\\ \cos\phi=\omega\cdot T \end{aligned} \]

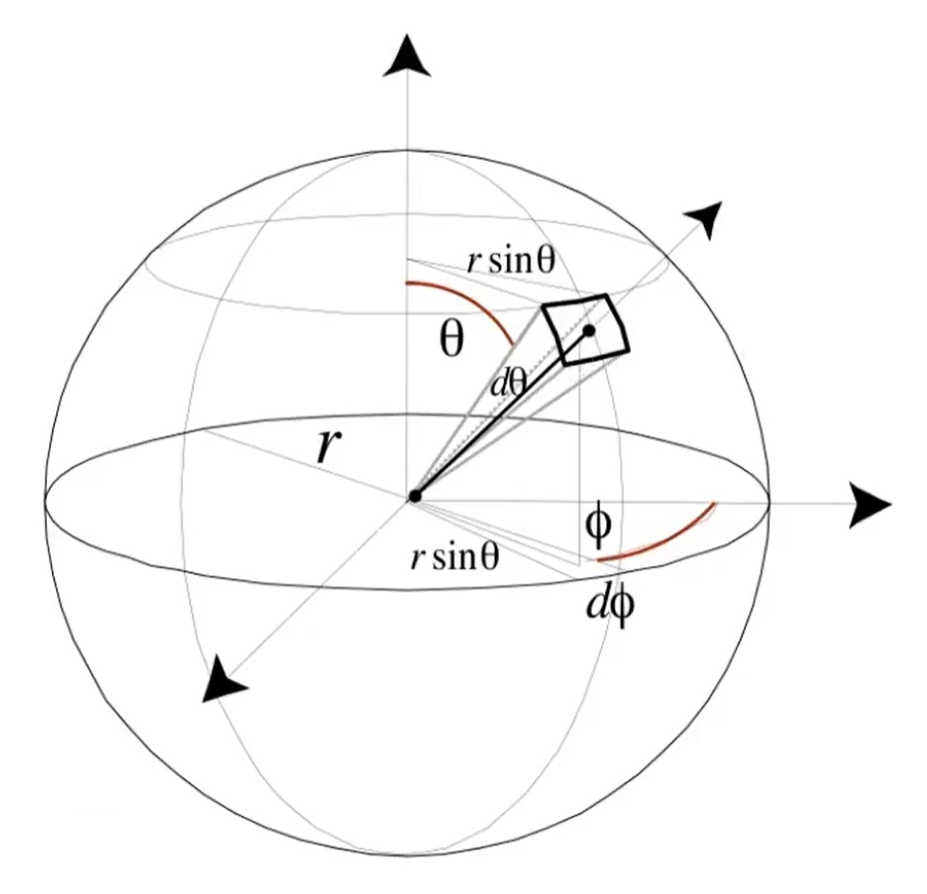
由于立体角是一种面积度量，这里使用微元法分析面积即可自然得到微分立体角的表示。微分立体角可表示为

\[d\sigma(\omega)\equiv\ \sin\theta\ d\theta\ d\phi\equiv\ d(-\cos\theta)\ d\phi \]

微分投影立体角也可以表示为多种形式

\[\begin{aligned} d\sigma^\perp(\omega) &\equiv|\cos\theta|\sin\theta\ d\theta\ d\phi\\ &\equiv|\cos\theta|\ d(-\cos\theta)\ d\phi\\ &\equiv\sin\theta\ d\sin\theta\ d\phi\\ &\equiv{1\over2}\ d(-\cos^2\theta)\ d\phi\\ &\equiv{1\over2}\ d\sin^2\theta\ d\phi \end{aligned} \]

即

\[\int_{S^2}\ d\sigma^\perp(\omega_i)=\int_0^{2\pi}\int_0^\pi|\cos\theta|\sin\theta\ d\theta\ d\phi \]

由此，scattering equation可以改写为

\[L_o(\theta_o,\phi_o)=\int_0^{2\pi}\int_0^\pi L_i(\theta_i,\phi_i)f_s(\theta_i,\phi_i,\theta_o,\phi_o)|\cos\theta_i|\sin\theta\ d\theta_i\ d\phi_i \]

虽然引入了参数化的角度表示，但向量表示仍有其优势

• 首先 \((\theta,\phi)\)​ 是一个局部的方向表示，因为这两个角度都依赖于表面法线
• 在涉及多个表面点的分析中，采用参数表示并不直观
• 参数表示引入了三角函数项，而这部分实际上又是由向量点积实现的
• 参数表示还依赖于切向量 \(T\) 以规定一个初始的azimuthal angle，而这并没有任何物理意义