BZOJ 1041 [HAOI2008]圆上的整点：数学【费马平方和定理】
题目链接：http://www.lydsy.com/JudgeOnline/problem.php?id=1041
题意：
给定n(n <= 2*10^9)，问你在圆x^2 + y^2 = n^2的圆周上，有多少个坐标为整数的点。
题解：
科普视频：http://www.bilibili.com/video/av12131743/
推导的大致思路：
推导：
一、17 = 4^2 + 1^2
求圆周上有多少个点，就是求有多少个整数对(a,b)满足a^2 + b^2 = R^2。
二、17 = (4+i)*(4-i)
变形：a^2 + b^2 = (a + b*i) * (a - b*i) = R^2。
其中，a + b*i 与 a - b*i 复共轭。
也就是将R^2分解成(a + b*i) * (a - b*i)。
有一个结论，对于整数a来说：
（1）如果a为4n + 1型的素数，则a可以被分解为两个不同的高斯素数。
（2）如果a为4n + 3型的素数，则不能被分解。因为它们不仅是普通素数，还是高斯素数。
（即费马平方和定理：只有4n+1型的素数，才能表示成两个数的平方和）
分解方法：
（1）首先将R^2分解质因数，R^2 = a1^p1 + a2^p2 +...
（2）然后将R^2继续分解成若干高斯素数之积。
（3）将这些高斯素数分成两组，如果这两组各自之积复共轭，则为一对合法的(a,b)。
其中，将高斯素数分组时，对于一个素因子ai，有pi+1中分组方法。
特别地，2^k对于最终答案没有影响。
根据乘法原理，在能够分组（分成复共轭数）的前提下，最终的分组方法数 = 4*∏(pi+1)。
（这就是本题的做法。分解质因数，复杂度O(sqrt(N))）
三、积性函数χ(n)，求π的表达式（这部分跟此题无关）
对于函数χ(n)，定义为：
（1）n = 4k + 1时，χ(n) = 1
（2）n = 4k + 3时，χ(n) = -1
（3）n为偶数时，χ(n) = 0
函数χ(n)对于任意整数满足性质：χ(ab) = χ(a)*χ(b)，所以χ(n)为积性函数。
将圆上点的数量写成如下形式：
即：N = 4*∏(∑ χ(ki))，ki为R^2的因子。
将上式拆开，每一项χ(n)的n为R的因子：
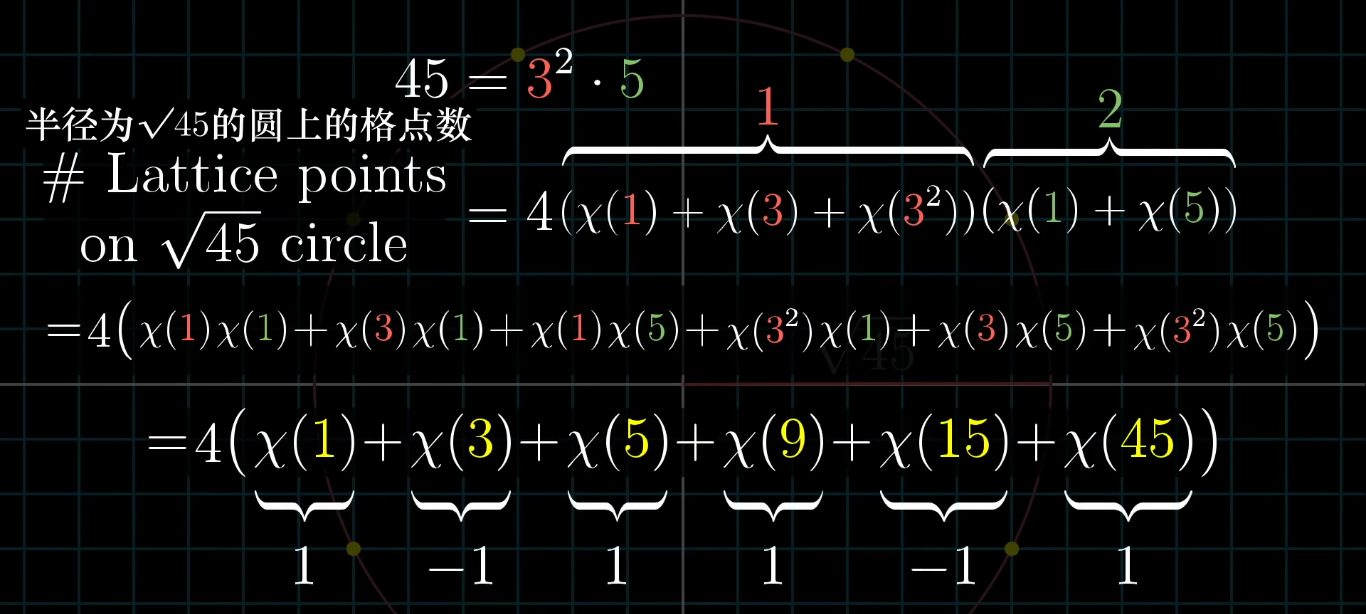
圆内所有点的个数：
移动之后：
所以得到了圆内点的个数，也就是圆面积的另一种表达形式。
最终得到了一个π的表达式。
AC Code:
1 #include <iostream> 2 #include <stdio.h> 3 #include <string.h> 4 5 using namespace std; 6 7 long long n; 8 long long ans=1; 9 10 int main() 11 { 12 cin>>n; 13 n=n*n; 14 long long t=n; 15 while(!(t&1)) t>>=1; 16 for(int i=3;i*i<=n && t>1;i++) 17 { 18 int p=0; 19 while(t%i==0) 20 { 21 p++; 22 t/=i; 23 } 24 if(i%4==1) ans*=(p+1); 25 else if(i%4==3 && (p&1)) 26 { 27 ans=0; 28 break; 29 } 30 } 31 if(t%4==3) ans=0; 32 cout<<ans*4<<endl; 33 }
