图论总结
Floyd
求无向图最小环问题
https://www.acwing.com/problem/content/346/
floyd是典型的插点算法,每次插入点k,为此,在点k被[插入前]可计算i-j-k这个环
即此时中间节点为:1~k-1,即我们已经算出了任意i<->j的最短道路,中间经过的节点可以为 (1,2,3,...,k-1)
我们只需枚举所有以k为环中最大节点的环即可。
pos[i][j]:i~j的最短路中经过的点是k(即由这个状态转移过来),且这个k是此路径中编号最大的点(除i,j)

const int N = 105; int n, m; int d[N][N], g[N][N]; int pos[N][N]; int path[N], cnt; void get_path(int i, int j) { if (!pos[i][j]) return; int k = pos[i][j]; get_path(i, k); path[cnt ++] = k; get_path(k, j); } int main() { cin >> n >> m; memset(g, 0x3f, sizeof g); while (m --) { int a, b, c; cin >> a >> b >> c; g[a][b] = g[b][a] = min(g[a][b], c); } int ans = INF; memcpy(d, g, sizeof d); for (int k = 1; k <= n; k ++) { // 枚举以k为最大编号的环 for (int i = 1; i < k; i ++) for (int j = i + 1; j < k; j ++) if ((LL)d[i][j] + g[i][k] + g[k][j] < ans) { // i->k->j->..->i ans = d[i][j] + g[i][k] + g[k][j]; cnt = 0; path[cnt ++] = k; path[cnt ++] = i; get_path(i, j); path[cnt ++] = j; } for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) if (d[i][j] > d[i][k] + d[k][j]) { d[i][j] = d[i][k] + d[k][j]; pos[i][j] = k; } } if (ans == INF) puts("No solution."); else { for (int i = 0; i < cnt; i ++) cout << path[i] << " \n"[i == cnt - 1]; } return 0; }
求从起点到终点恰好经过k(很多)条边的问题(可以包含负环)
https://www.acwing.com/problem/content/347/(边数<=100,点数<=200,恰好经过边数<=1e6)
原Floyd状态表示为 d[k, i, j] : 从 i -> j 只经过 1 ~ k 的话的最短路径
本题状态表示为 d[k, i, j] : 从 i -> j 恰好经过 k 条边的最短路径,但是第一维优化掉了。
用倍增的方法枚举边数 N 的二进制1, g 数组走的恰好边数为1 -> 2 -> 4 ...
g[i][j] 为走恰好当前边时 i -> j 的最短距离

const int N = 205; int k, n, m, S, E; int g[N][N], ans[N][N]; void floyd(int c[][N], int a[][N], int b[][N]) { int temp[N][N]; memset(temp, 0x3f, sizeof temp); for (int k = 1; k <= n; k ++) for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) temp[i][j] = min(temp[i][j], a[i][k] + b[k][j]); memcpy(c, temp, sizeof temp); } void qmi() { memset(ans, 0x3f, sizeof ans); for (int i = 1; i <= n; i ++) ans[i][i] = 0; while (k) { if (k & 1) floyd(ans, ans, g); // ans = ans + g; floyd(g, g, g); k >>= 1; } } int main() { cin >> k >> m >> S >> E; memset(g, 0x3f, sizeof g); unordered_map<int, int> idx; if (!idx.count(S)) idx[S] = ++ n; if (!idx.count(E)) idx[E] = ++ n; S = idx[S], E = idx[E]; while (m --) { int a, b, c; cin >> c >> a >> b; if (!idx.count(a)) idx[a] = ++ n; if (!idx.count(b)) idx[b] = ++ n; a = idx[a], b = idx[b]; g[a][b] = g[b][a] = min(g[a][b], c); } qmi(); cout << ans[S][E] << endl; return 0; }
最小生成树
求(严格)次小生成树问题
https://www.acwing.com/problem/content/1150/
(1)1.求最小生成树,标记每条边为树边还是非树边,2预处理最小生成树中任意两点间的最大边权和严格次大边权(非严格次小生成树不需要),3.依次枚举所有非树边

const int N = 505, M = 1e4 + 5; struct Edge { int a, b, w; bool f; bool operator< (const Edge &W) const { return w < W.w; } }edge[M]; int n, m; int p[N], dist1[N][N], dist2[N][N]; int h[N], e[N * 2], ne[N * 2], w[N * 2], idx;//维护的是最小生成树边权 int find(int x) { if (p[x] != x) p[x] = find(p[x]); return p[x]; } void add(int a, int b, int c) { e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++; } void dfs(int u, int fa, int maxd1, int maxd2, int d1[], int d2[]) { d1[u] = maxd1, d2[u] = maxd2; for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (j == fa) continue; int t1 = maxd1, t2 = maxd2; if (w[i] > t1) t2 = t1, t1 = w[i]; else if (w[i] < t1 && w[i] > t2) t2 = w[i]; dfs(j, u, t1, t2, d1, d2); } } int main() { cin >> n >> m; memset(h, -1, sizeof h); for (int i = 0; i < m; i ++) { int a, b, c; cin >> a >> b >> c; edge[i] = {a, b, c}; } sort(edge, edge + m); LL sum = 0;//kruskal for (int i = 1; i <= n; i ++) p[i] = i; for (int i = 0; i < m; i ++) { int a = edge[i].a, b = edge[i].b, w = edge[i].w; int pa = find(a), pb = find(b); if (pa != pb) { sum += w; p[pa] = pb; edge[i].f = true; add(a, b, w), add(b, a, w); } } LL ans = 9e18; for (int i = 1; i <= n; i ++) dfs(i, -1, 0, 0, dist1[i], dist2[i]); for (int i = 0; i < m; i ++)//枚举所有非树边 if (!edge[i].f) { int a = edge[i].a, b = edge[i].b, w = edge[i].w; if (w > dist1[a][b]) ans = min(ans, sum - dist1[a][b] + w);//保证严格次小 else if (w > dist2[a][b]) ans = min(ans, sum - dist2[a][b] + w); } cout << ans << endl; return 0; }
(2)用 kruskal + lca (时间复杂度更低)

const int N = 1e5 + 5, M = 3e5 + 5; struct Edge { int a, b, c; bool used; bool operator< (const Edge &W) const { return c < W.c; } }edge[M]; int n, m; int h[N], e[M], ne[M], w[M], idx; int depth[N], fa[N][17], d1[N][17], d2[N][17];//分别存最大边和次大边 int p[N], q[N]; void add(int a, int b, int c) int find(int x) LL kruskal() { for (int i = 1; i <= n; i ++) p[i] = i; sort(edge, edge + m); LL ans = 0; for (int i = 0; i < m; i ++) { int a = edge[i].a, b = edge[i].b, w = edge[i].c; int pa = find(a), pb = find(b); if (pa != pb) { ans += w; p[pa] = pb; edge[i].used = true; } } return ans; } void build() {//给最小生成树建边 memset(h, -1, sizeof h); for (int i = 0; i < m; i ++) if (edge[i].used) { auto t = edge[i]; add(t.a, t.b, t.c), add(t.b, t.a, t.c); } } void bfs() { memset(depth, 0x3f, sizeof depth); depth[0] = 0, depth[1] = 1; int hh = 0, tt = 0; q[0] = 1; //假定1为根 while (hh <= tt) { int t = q[hh ++]; for (int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if (depth[j] > depth[t] + 1) { depth[j] = depth[t] + 1; q[++ tt] = j; fa[j][0] = t; d1[j][0] = w[i], d2[j][0] = -INF; for (int k = 1; k <= 16; k ++) { int anc = fa[j][k - 1]; fa[j][k] = fa[anc][k - 1]; int d[4] = {d1[j][k - 1], d2[j][k - 1], d1[anc][k - 1], d2[anc][k - 1]}; d1[j][k] = d2[j][k] = -INF; for (int u = 0; u < 4; u ++) if (d[u] > d1[j][k]) d2[j][k] = d1[j][k], d1[j][k] = d[u]; else if (d[u] > d2[j][k]) d2[j][k] = d[u]; } } } } } int lca(int a, int b, int w) { int d[N * 2]; int cnt = 0; if (depth[a] < depth[b]) swap(a, b); for (int k = 16; ~k; k --) if (depth[fa[a][k]] >= depth[b]) { d[cnt ++] = d1[a][k]; d[cnt ++] = d2[a][k]; a = fa[a][k]; } if (a != b) { for (int k = 16; ~k; k --) if (fa[a][k] != fa[b][k]) { d[cnt ++] = d1[a][k]; d[cnt ++] = d2[a][k]; d[cnt ++] = d1[b][k]; d[cnt ++] = d2[b][k]; a = fa[a][k], b = fa[b][k]; } d[cnt ++] = d1[a][0]; d[cnt ++] = d1[b][0]; } int dist1 = -INF, dist2 = -INF; for (int i = 0; i < cnt; i ++) { int x = d[i]; if (x > dist1) dist2 = dist1, dist1 = x; else if (x != dist1 && x > dist2) dist2 = x; } if (w > dist1) return w - dist1; if (w > dist2) return w - dist2; return INF; } int main() { cin >> n >> m; for (int i = 0; i < m; i ++) { int a, b, c; cin >> a >> b >> c; edge[i] = {a, b, c}; } LL sum = kruskal(); build(); bfs(); LL ans = 9e18; for (int i = 0; i < m; i ++) if (!edge[i].used) { auto t = edge[i]; ans = min(ans, lca(t.a, t.b, t.c) + sum); } cout << ans << endl; return 0; }
负环
(dist数组可以不初始化,但是不一定会变快,一般初始化为0)
二分答案(double),将点权加在边权上并求是否存在正环
spfa可以求最长路
https://www.acwing.com/problem/content/363/
求正环可以把边权取反,也可以求最长路

const int N = 1e3 + 5, M = 5e3 + 5; int n, m; int wp[N]; int h[N], e[M], ne[M], we[M], idx; double dist[N]; int q[N], cnt[N]; bool st[N]; void add(int a, int b, int c) { e[idx] = b, we[idx] = c, ne[idx] = h[a], h[a] = idx ++; } bool spfa(double mid) { memset(dist, 0, sizeof dist); memset(st, 0, sizeof st); memset(cnt, 0, sizeof cnt); int hh = 0, tt = 0; for (int i = 1; i <= n; i ++) q[tt ++] = i, st[i] = true; while (hh != tt) { int t = q[hh ++]; if (hh == N) hh = 0; st[t] = false; for (int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if (dist[j] < dist[t] + wp[t] - mid * we[i]) {//最长路求是否有正环 dist[j] = dist[t] + wp[t] - mid * we[i]; cnt[j] = cnt[t] + 1; if (cnt[j] >= n) return true; if (!st[j]) { q[tt ++] = j; if (tt == N) tt = 0; st[j] = true; } } } } return false; } int main() { cin >> n >> m; for (int i = 1; i <= n; i ++) cin >> wp[i]; memset(h, -1, sizeof h); while (m --) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } double l = 0, r = 1000; while (r - l > 1e-4) { double mid = (l + r) / 2; if (spfa(mid)) l = mid; else r = mid; } printf("%.2lf", l); return 0; }
差分约束
求最小值为最长路(a >= b + x),最大值为最短路(a <= b + x)
如果spfa用队列TLE,可以尝试把队列改成栈
最小值:最长路,形式 A >= B + C, 建边 B -> A 边权为 C
最近公共祖先(LCA)
(1)向上标记法 O(n)
(2) 倍增
fa[i, j] 表示从 i 开始, 向上走 2^j 步所能走到的节点, 0 <= j <= log n
depth[i]表示深度
哨兵:如果从 i 开始跳 2^j 步会跳过根节点,那么 fa[i, j] = 0, depth[0] = 0
步骤: [1] 先将两个点跳到同一层 [2] 让两个点同时往上跳, 一直跳到它们的最近公共祖先的下一层
预处理 :O(nlogn) 查询 :O(logn)
(3)Tarjan---离线求LCA O(n + m)
在深度优先遍历时将所有点分成三大类
[1] 已经遍历过, 且回溯过的点(2) [2] 正在搜索的点(1) [3] 还未搜索的点(0)
步骤: [1] 先求出所有点到根结点的距离dist[],设x号点和y号点的最近公共祖先是p,则x和y的最近距离等于dist[x] + dist[y] - 2 * dist[p]
[2] 在深度优先遍历1号点中的u点的时候,需要把u的查询的另外一个点的最短距离进行计算并存储,最后把u点合并到上一结点的集合
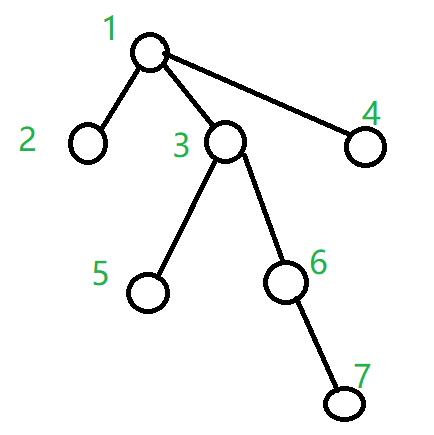
例如当前正在搜索1->3->6,5被搜索过了,那么st[5] = 2, p[5] = 3, p[3] = 3(还未更新)
倍增代码:
题目大意:给定一棵无向树, 再给m个询问,每个询问有a, b, 若lca(a, b) = a输出1, lca(a,b) = b 输出2, 否则输出0

const int N = 4e4 + 5, M = N * 2; int n, m; int h[N], e[M], ne[M], idx; int depth[N], fa[N][16]; int q[N]; void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx ++; } void bfs(int root) {//处理depth和fa memset(depth, 0x3f, sizeof depth); depth[0] = 0, depth[root] = 1; int hh = 0, tt = 0; q[0] = root; while (hh <= tt) { int t = q[hh ++]; for (int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if (depth[j] > depth[t] + 1) { depth[j] = depth[t] + 1; q[++ tt] = j; fa[j][0] = t; for (int k = 1; k <= 15; k ++) fa[j][k] = fa[fa[j][k - 1]][k - 1]; } } } } int lca(int a, int b) { if (depth[a] < depth[b]) swap(a, b); for (int k = 15; ~k; k --) if (depth[fa[a][k]] >= depth[b]) a = fa[a][k]; if (a == b) return a; for (int k = 15; ~k; k --) if (fa[a][k] != fa[b][k]) { a = fa[a][k]; b = fa[b][k]; } return fa[a][0]; } int main() { int root; cin >> n; memset(h, -1, sizeof h); for (int i = 1; i <= n; i ++) { int a, b; cin >> a >> b; if (b == -1) root = a; else add(a, b), add(b, a); } bfs(root); cin >> m; while (m --) { int a, b; cin >> a >> b; int anc = lca(a, b); if (anc == a) cout << 1 << endl; else if (anc == b) cout << 2 << endl; else cout << 0 << endl; } return 0; }
Tarjan代码
题目大意: n 个点的无向树,多次询问两点之间的最短距离
https://www.acwing.com/problem/content/1173/

const int N = 1e4 + 5, M = 2 * N; int n, m; int h[N], e[M], ne[M], w[M], idx; int dist[N], p[N]; int ans[M], st[N]; vector<PII> query[N];//first存查询的另一个点,second存查询编号 void add(int a, int b, int c) { e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++; } int find(int x) { if (p[x] != x) p[x] = find(p[x]); return p[x]; } void dfs(int u, int fa) { for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (j == fa) continue; dist[j] = dist[u] + w[i]; dfs(j, u); } } void tarjan(int u) { st[u] = 1; for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (!st[j]) { tarjan(j);//标记 p[j] = u; } } for (auto it : query[u]) { int point = it.fx, id = it.fy; if (st[point] == 2) { int anc = find(point); ans[id] = dist[u] + dist[point] - 2 * dist[anc]; } } st[u] = 2; //回溯 } int main() { cin >> n >> m; memset(h, -1, sizeof h); for (int i = 1; i < n; i ++) { int a, b, c; cin >> a >> b >> c; add(a, b, c), add(b, a, c); } for (int i = 0; i < m; i ++) {//提前存储查询相关点 int a, b; cin >> a >> b; if (a != b) { query[a].ph({b, i}); query[b].ph({a, i}); } } for (int i = 1; i <= n; i ++) p[i] = i; dfs(1, -1);//假定1为根节点 tarjan(1); for (int i = 0; i < m; i ++) cout << ans[i] << endl; return 0; }
(4)先求树的欧拉序,求 x 和 y 的 LCA 就是 x y 欧拉序之间深度最小的点
有向图的强连通分量(SCC)
有向无环图(DAG)
按照拓扑序可以在DAG中求最长路最短路
Tarjan算法求SCC
对每个点定义两个时间戳 dfn[u] 表示遍历到 u 的时间戳, low[u] 表示从 u 开始走所能遍历的最大时间戳, 若 u 是其所在强连通分量的最低点则 dfn[u] = low[u]
Tarjan算法之后连通块编号点的顺序就是拓扑序
给定一个有向图连通图请问最少加几条边可以把它变成强连通分量
结论: max{p, q}, p 为缩点后入度为 0 的点, q 为缩点后出度为 0 的点
题目大意:将强连通分量缩点后,若出点为0的强连通分量只有一个输出该大小否则输出0

const int N = 1e4 + 5, M = 5e4 + 5; int n, m; int h[N], e[M], ne[M], w[M], idx; int dfn[N], low[N], timestamp; int stk[N], top; bool in_stk[N]; int id[N], scc_cnt, Size[N]; int dout[N]; void add(int a, int b) void tarjan(int u) { dfn[u] = low[u] = ++timestamp; stk[++ top] = u, in_stk[u] = true; for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (!dfn[j]) { tarjan(j); low[u] = min(low[u], low[j]); } else if (in_stk[j]) low[u] = min(low[u], dfn[j]); //注意不是else } if (dfn[u] == low[u]) { ++ scc_cnt; int y; do { y = stk[top --]; in_stk[y] = false; id[y] = scc_cnt; Size[scc_cnt] ++; } while (y != u); } } int main() { cin >> n >> m; memset(h, -1, sizeof h); while (m --) { int a, b; cin >> a >> b; add(a, b); } for (int i = 1; i <= n; i ++) if (!dfn[i]) tarjan(i); for (int i = 1; i <= n; i ++) for (int j = h[i]; ~j; j = ne[j]) { int k = e[j]; int a = id[i], b = id[k]; if (a != b) dout[a] ++; } int sum = 0, ans; for (int i = 1; i <= scc_cnt; i ++) if (!dout[i]) { sum ++; ans = Size[i]; if (sum > 1) { ans = 0; break; } } cout << ans << endl; return 0; }
无向图的双(重)连通分量
边双连通分量 e-DCC :极大的不含有桥的连通块
点双连通分量 v-DCC:极大的不含有割点的连通块
桥:若删去此边则原本连通分量变的不连通, x-y为桥相当于dfn[x] < low[y]
割点:若删去此点则原本连通分量变的不连通
如何求割点, x - y ,(1)若 x 不是根节点且 low(y) >= dfn(x) 则 x 是割点 (2) 若 x 是根节点,若至少有两个子节点 y 满足 low(y) >= dfn(x) , 则 x 是割点
题目大意:给定一个无向连通图请问最少加几条边可以把它变成双连通分量
结论: (cnt + 1) / 2 , cnt 为缩点后度数为 1 的点的数量

const int N = 5e3 + 5, M = 2e4 + 5; int n, m; int h[N], e[M], ne[M], idx; int dfn[N], low[N], timestamp; int stk[N], top; int id[N], dcc_cnt; bool is_bridge[M]; int d[N]; void add(int a, int b) void tarjan(int u, int from) { dfn[u] = low[u] = ++ timestamp; stk[++ top] = u; for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (!dfn[j]) { tarjan(j, i); low[u] = min(low[u], low[j]); if (dfn[u] < low[j]) is_bridge[i] = is_bridge[i ^ 1] = true; } else if (i != (from ^ 1)) low[u] = min(low[u], dfn[j]); } if (dfn[u] == low[u]) { ++ dcc_cnt; int y; do { y = stk[top --]; id[y] = dcc_cnt; } while (y != u); } } int main() { cin >> n >> m; memset(h, -1, sizeof h); while (m --) { int a, b; cin >> a >> b; add(a, b), add(b, a); } tarjan(1, -1);//以任意一点作为根节点 for (int i = 0; i < idx; i ++) if (is_bridge[i]) { d[id[e[i]]] ++; } int cnt = 0; for (int i = 1; i <= dcc_cnt; i ++) if (d[i] == 1) cnt ++; cout << (cnt + 1) / 2 << endl; return 0; }
题目大意:给定一个由 n 个点 m 条边构成的无向图,请你求出该图删除一个点之后,连通块最多有多少。

const int N = 1e4 + 5, M = 3e4 + 5; int n, m; int h[N], e[M], ne[M], idx; int dfn[N], low[N], timestamp; int root, ans; void add(int a, int b) void tarjan(int u) { dfn[u] = low[u] = ++ timestamp; int cnt = 0;//cnt为删去u这个点后可以得到的连通块数量 for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (!dfn[j]) { tarjan(j); low[u] = min(low[u], low[j]); if (low[j] >= dfn[u]) cnt ++; } else low[u] = min(low[u], dfn[j]); } if (u != root) cnt ++; ans = max(ans, cnt); } int main() { while (cin >> n >> m, n || m) { memset(dfn, 0, sizeof dfn); memset(h, -1, sizeof h); idx = timestamp = 0; while (m --) { int a, b; cin >> a >> b; add(a, b), add(b, a); } ans = 0;//ans为删去一个点后可以得到的最大连通块 int cnt = 0;//cnt为连通块的数量 for (root = 0; root < n; root ++) if (!dfn[root]) { cnt ++; tarjan(root); } cout << ans + cnt - 1 << endl; } return 0; }
二分图
染色法
题目大意:求构成的二分图中两部分中边的最大值的最小值

const int N = 2e4 + 5, M = 2e5 + 5; int n, m; int h[N], e[M], ne[M], w[M], idx; int color[N]; void add(int a, int b, int c) bool dfs(int u, int c, int mid) { color[u] = c; for (int i = h[u]; ~i; i = ne[i]) { int j = e[i]; if (w[i] <= mid) continue; if (color[j]) { if (color[j] == c) return false; } else if (!dfs(j, 3 - c, mid)) return false; } return true; } bool check(int mid) { memset(color, 0, sizeof color); for (int i = 1; i <= n; i ++) if (!color[i]) if (!dfs(i, 1, mid)) return false; return true; } int main() { cin >> n >> m; memset(h, -1, sizeof h); while (m --) { int a, b, c; cin >> a >> b >> c; add(a, b, c), add(b, a, c); } int l = 0, r = 1e9; while (l < r) { int mid = l + r >> 1; if (check(mid)) r = mid; else l = mid + 1; } cout << l << endl; return 0; }
匈牙利算法
二分图的前提下:
最大匹配数 = 最小点覆盖 = 总点数 - 最大独立集 = 总点数 - 最小路径点覆盖
最大匹配等价于不存在增广路径,意思是最多连多少条边, 且所有的边无公共点
最大独立集:选出最多的点,使得选出的点之间没有边
最小点覆盖:使得每一条边的两个端点中至少有一个点被选中
最小路径点覆盖:对于DAG,用最少的互不相交的路径将所有点覆盖
题目大意:给定一个n*n的棋盘,问最多能在棋盘中摆放多少长为2宽为1的牌(有些位置不能放置)。可转化为一个小方格若可以和其他方格形成牌子则连一条边,那么题目是求棋盘中最多取多少个边且没有公共点(求最大匹配)

const int N = 105; int n, m; PII match[N][N]; bool g[N][N], st[N][N]; int dx[4] = {-1, 0, 1, 0}; int dy[4] = {0, 1, 0, -1}; bool find(int x, int y) { for (int i = 0; i < 4; i ++) { int a = x + dx[i], b = y + dy[i]; if (a < 1 || a > n || b < 1 || b > n) continue; if (g[a][b] || st[a][b]) continue; st[a][b] = true; PII t = match[a][b]; if (t.fx == -1 || find(t.fx, t.fy)) { match[a][b] = {x, y}; return true; } } return false; } int main() { cin >> n >> m; while (m --) { int a, b; cin >> a >> b; g[a][b] = true;//该方格不能放置 } memset(match, -1, sizeof match); int ans = 0; for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) if ((i + j) % 2 && !g[i][j]) { memset(st, 0, sizeof st); if (find(i, j)) ans ++; } cout << ans << endl; return 0; }
题目大意:求最小点覆盖(ai-bi这条边中的端点ai,bi至少取一个),相当于求最大匹配(做的时候可能感觉做法与题意不同,但是结果是ac的,因为最小点覆盖=最大匹配)、
题目大意:在一个棋盘中放马,但是没有蹩马腿的规则,问最多可以放多少马,但是一些格子坏了。相当于求最大独立集 = n * m - k - 最大匹配,k为坏了的各自的数量
题目大意:给出一个DAG,求出最多的点使得从任意一个点出发都走不到其他点。答案 :最小路径点覆盖 = n - 最大匹配

const int N = 205; int n, m; int match[N]; bool d[N][N], st[N]; bool find(int x) { for (int i = 1; i <= n; i ++) if (d[x][i] && !st[i]) {//求最大匹配 st[i] = true; if (match[i] == 0 || find(match[i])) { match[i] = x; return true; } } return false; } int main() { cin >> n >> m; while (m --) { int a, b; cin >> a >> b; d[a][b] = true; } //传递闭包floyd for (int k = 1; k <= n; k ++) for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) d[i][j] |= d[i][k] & d[k][j]; int ans = 0; for (int i = 1; i <= n; i ++) { memset(st, 0, sizeof st); if (find(i)) ans ++; } cout << n - ans << endl; return 0; }
欧拉路径与欧拉回路
一、无向图
1 存在欧拉路径的充要条件 : 度数为奇数的点只能有0或2个
2 存在欧拉回路的充要条件 : 度数为奇数的点只能有0个
二、有向图
1 存在欧拉路径的充要条件 : 要么所有点的出度均==入度;要么除了起点终点之外,其余所有点的出度==入度 ,一个满足出度-入度==1(起点) 一个满足入度-出度==1(终点)
2 存在欧拉回路的充要条件 : 所有点的出度均等于入度
题目大意:在图中找一个环使得每条边都在环上出现恰好一次。(t=1无向图,t=2有向图),若有则输出所有边的编号
注意一定要把 u 的所有可达点遍历之后再把u加进去

const int N = 100010, M = 400010; int type; int n, m; int h[N], e[M], ne[M], idx; bool used[M]; int ans[M], cnt; int din[N], dout[N]; void add(int a, int b) void dfs(int u) { for (int &i = h[u]; ~i;) { if (used[i]) { i = ne[i]; continue; } used[i] = true; if (type == 1) used[i ^ 1] = true; int t; if (type == 1) { t = i / 2 + 1; if (i & 1) t = -t; } else t = i + 1; int j = e[i]; i = ne[i]; dfs(j); ans[ ++ cnt] = t; } } int main() { scanf("%d", &type); scanf("%d%d", &n, &m); memset(h, -1, sizeof h); for (int i = 0; i < m; i ++ ) { int a, b; scanf("%d%d", &a, &b); add(a, b); if (type == 1) add(b, a); din[b] ++ , dout[a] ++ ; } if (type == 1) { for (int i = 1; i <= n; i ++ ) if (din[i] + dout[i] & 1) { puts("NO"); return 0; } } else { for (int i = 1; i <= n; i ++ ) if (din[i] != dout[i]) { puts("NO"); return 0; } } for (int i = 1; i <= n; i ++ ) if (h[i] != -1) { dfs(i); break; } if (cnt < m) { puts("NO"); return 0; } puts("YES"); for (int i = cnt; i; i -- ) printf("%d ", ans[i]); puts(""); return 0; }
拓扑排序
题目大意:给一张DAG,分别统计从每个点出发能够到达的点的数量。

const int N = 30010, M = 30010; int n, m; int h[N], e[M], ne[M], idx; int d[N], q[N]; bitset<N> f[N]; void add(int a, int b) void topsort() { int hh = 0, tt = -1; for (int i = 1; i <= n; i ++ ) if (!d[i]) q[ ++ tt] = i; while (hh <= tt) { int t = q[hh ++ ]; for (int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if ( -- d[j] == 0) q[ ++ tt] = j; } } } int main() { cin >> n >> m memset(h, -1, sizeof h); for (int i = 0; i < m; i ++ ) { int a, b; cin >> a >> b; add(a, b); d[b] ++ ; } topsort(); for (int i = n - 1; i >= 0; i -- ) { int j = q[i]; f[j][j] = 1; for (int k = h[j]; ~k; k = ne[k]) f[j] |= f[e[k]]; } for (int i = 1; i <= n; i ++ ) printf("%d\n", f[i].count()); return 0; }
求树中直径d1,d2,up边
https://www.acwing.com/problem/content/1080/

void dfs_d(int u, int fa) { for (int v : g[u]) { if (v == fa) continue; dfs_d(v, u); int dist = d1[v] + 1; if (dist >= d1[u]) { p[u] = v; d2[u] = d1[u], d1[u] = dist; } else if (dist > d2[u]) d2[u] = dist; } maxd = max(maxd, d1[u] + d2[u]); } void dfs_u(int u, int fa) { for (int v : g[u]) { if (v == fa) continue; up[v] = up[u] + 1; if (p[u] == v) up[v] = max(up[v], d2[u] + 1); else up[v] = max(up[v], d1[u] + 1); dfs_u(v, u); } }
const int N = 100010, M = 400010; int type; int n, m; int h[N], e[M], ne[M], idx; bool used[M]; int ans[M], cnt; int din[N], dout[N]; void add(int a, int b) void dfs(int u) { for (int &i = h[u]; ~i;) { if (used[i]) { i = ne[i]; continue; } used[i] = true; if (type == 1) used[i ^ 1] = true; int t; if (type == 1) { t = i / 2 + 1; if (i & 1) t = -t; } else t = i + 1; int j = e[i]; i = ne[i]; dfs(j); ans[ ++ cnt] = t; } } int main() { scanf("%d", &type); scanf("%d%d", &n, &m); memset(h, -1, sizeof h); for (int i = 0; i < m; i ++ ) { int a, b; scanf("%d%d", &a, &b); add(a, b); if (type == 1) add(b, a); din[b] ++ , dout[a] ++ ; } if (type == 1) { for (int i = 1; i <= n; i ++ ) if (din[i] + dout[i] & 1) { puts("NO"); return 0; } } else { for (int i = 1; i <= n; i ++ ) if (din[i] != dout[i]) { puts("NO"); return 0; } } for (int i = 1; i <= n; i ++ ) if (h[i] != -1) { dfs(i); break; } if (cnt < m) { puts("NO"); return 0; } puts("YES"); for (int i = cnt; i; i -- ) printf("%d ", ans[i]); puts("");



 浙公网安备 33010602011771号
浙公网安备 33010602011771号