模板代码

字典树模板+初始化模板

https://codeforces.com/contest/1658/problem/D2

int l, r;
int son[M][2], idx;
int a[N];

void init() {//初始化**
    idx = 0;
    son[0][0] = son[0][1] = 0;
}

void insert(int x) {
    int p = 0;
    for (int i = 30; ~i; i --) {
        int &v = son[p][x >> i & 1];
        if (!v) {
            son[idx + 1][0] = son[idx + 1][1] = 0;//初始化*****
            v = ++ idx;
        }
        p = v;
    }
}

int findmax(int x) {
    int p = 0, ans = 0;
    for (int i = 30; ~i; i --) {
        int v = x >> i & 1;
        if (son[p][!v]) {
            ans += 1 << i;
            p = son[p][!v];
        }
        else p = son[p][v];
    }
    return ans;
}

int findmin(int x) {
    int p = 0, ans = 0;
    for (int i = 30; ~i; i --) {
        int v = x >> i & 1;
        if (son[p][v]) p = son[p][v];
        else {
            ans += 1 << i;
            p = son[p][!v];
        }
    }
    return ans;
}

void solve() {
    cin >> l >> r;

    init();
    for (int i = l; i <= r; i ++) cin >> a[i], insert(a[i]);

    for (int i = l; i <= r; i ++) {
        int x = a[i] ^ l;

        if (findmin(x) == l && findmax(x) == r) {
            cout << x << endl;
            return;
        }
    }

 MEX模板

https://codeforces.com/contest/1629/problem/C

struct MEX {
    set<int> hash;
    multiset<int> mhash;
    int cnt[N];
 
    void init() {
        for (int i = 0; i < N; i ++) cnt[i] = 0, hash.insert(i);
    }
    void add(int x) {
        if (!cnt[x]) hash.erase(x);
 
        cnt[x] ++;
        mhash.insert(x);
    }
    void del(int x) {
        if (cnt[x] == 1) hash.insert(x);
        
        cnt[x] --;
        mhash.erase(mhash.find(x));
    }
    int mex() {
        return *hash.begin();
    }
    void clear() {
        while (mhash.size()) del(*mhash.begin());
    }
};

 计算几何模板

const double eps = 1e-9;
const double pi = acos(-1);
  
inline int sign(double a) { return a < -eps ? -1 : a > eps; }
  
inline int cmp(double a, double b){ return sign(a - b); }
  
struct Point {
    double x, y;
    Point() {}
    Point(double _x, double _y) : x(_x), y(_y) {}
    Point operator+(Point p) { return {x + p.x, y + p.y}; }
    Point operator-(Point p) { return {x - p.x, y - p.y}; }
    Point operator*(double d) { return {x * d, y * d}; }
    Point operator/(double d) { return {x / d, y / d}; }
    double operator* (const Point& b) const { return x * b.x + y * b.y; }//点积
    double operator& (const Point& b) const { return x * b.y - y * b.x; }//叉积

    bool operator<(Point p) const { 
        int c = cmp(x, p.x);
        if (c) return c == -1;
        return cmp(y, p.y) == -1;
    }

    bool operator==(Point o) const{
        return cmp(x,o.x) == 0 && cmp(y,o.y) == 0;
    }

    void read() {cin >> x >> y;}
    void print() {cout << x << ' ' << y << endl;}
     
    double distTo(Point p) { return (*this-p).len(); }//求两点之间的距离
    double len() { return sqrt(len2());}//模长
    double len2() { return x * x + y * y; }//模长的平方
    Point rot90() { return Point(-y, x);}//逆时针转 90°
    Point unit() { return *this / len(); }//方向向量
    Point rot(double an){ return {x * cos(an) - y * sin(an), x * sin(an) + y * cos(an)}; }//逆时针转一个弧度，不是角度
};

#define cross(p1,p2,p3) ((p2.x-p1.x)*(p3.y-p1.y)-(p3.x-p1.x)*(p2.y-p1.y))
#define crossOp(p1,p2,p3) sign(cross(p1,p2,p3))
 
// 直线 p1p2, q1q2 是否恰有一个交点
bool chkLL(Point p1, Point p2, Point q1, Point q2) {
    double a1 = cross(q1, q2, p1), a2 = -cross(q1, q2, p2);
    return sign(a1+a2) != 0;
}

// 求直线 p1p2, q1q2 的交点
Point isLL(Point p1, Point p2, Point q1, Point q2) {
    double a1 = cross(q1, q2, p1), a2 = -cross(q1, q2, p2);
    return (p1 * a2 + p2 * a1) / (a1 + a2);
}

// 判断区间 [l1, r1], [l2, r2] 是否相交
bool intersect(double l1,double r1,double l2,double r2){
    if (l1>r1) swap(l1,r1); if (l2>r2) swap(l2,r2); 
    return !( cmp(r1,l2) == -1 || cmp(r2,l1) == -1 );
}

// 线段 p1p2, q1q2 相交
bool isSS(Point p1, Point p2, Point q1, Point q2){
    return intersect(p1.x,p2.x,q1.x,q2.x) && intersect(p1.y,p2.y,q1.y,q2.y) && 
    crossOp(p1,p2,q1) * crossOp(p1,p2,q2) <= 0 && crossOp(q1,q2,p1)
            * crossOp(q1,q2,p2) <= 0;
}

// 线段 p1p2, q1q2 严格相交  
bool isSS_strict(Point p1, Point p2, Point q1, Point q2){
    return crossOp(p1,p2,q1) * crossOp(p1,p2,q2) < 0 && crossOp(q1,q2,p1)
            * crossOp(q1,q2,p2) < 0;
}

// m 在 a 和 b 之间
bool isMiddle(double a, double m, double b) {
    /*if (a > b) swap(a, b);
    return cmp(a, m) <= 0 && cmp(m, b) <= 0;*/
    return sign(a - m) == 0 || sign(b - m) == 0 || (a < m != b < m);
}

bool isMiddle(Point a, Point m, Point b) {
    return isMiddle(a.x, m.x, b.x) && isMiddle(a.y, m.y, b.y);
}

// 点 p 在线段 p1p2 上
bool onSeg(Point p1, Point p2, Point q){
    return crossOp(p1,p2,q) == 0 && isMiddle(p1, q, p2);
}
// q1q2 和 p1p2 的交点 在 p1p2 上？

// 点 p 严格在 p1p2 上
bool onSeg_strict(Point p1, Point p2, Point q){
    return crossOp(p1,p2,q) == 0 && sign((q-p1)*(p1-p2)) * sign((q-p2)*(p1-p2)) < 0;
}

// 求 q 到 直线p1p2 的投影（垂足） ⚠️ : p1 != p2
Point proj(Point p1, Point p2, Point q) {
    Point dir = p2 - p1;
    return p1 + dir * ((dir * (q - p1)) / dir.len2());
}

// 求 q 以 直线p1p2 为轴的反射
Point reflect(Point p1, Point p2, Point q){
    return proj(p1,p2,q) * 2 - q;
}

// 求 q 到 线段p1p2 的最小距离
double nearest(Point p1, Point p2, Point q){
    if (p1 == p2) return p1.distTo(q);
    Point h = proj(p1,p2,q);
    if(isMiddle(p1,h,p2))
        return q.distTo(h);
    return min(p1.distTo(q),p2.distTo(q));
}

// 求 线段p1p2 与 线段q1q2 的距离
double disSS(Point p1, Point p2, Point q1, Point q2){
    if(isSS(p1,p2,q1,q2)) return 0;
    return min(min(nearest(p1,p2,q1),nearest(p1,p2,q2)), min(nearest(q1,q2,p1),nearest(q1,q2,p2)));
}

 数论分块模板

 

 

 

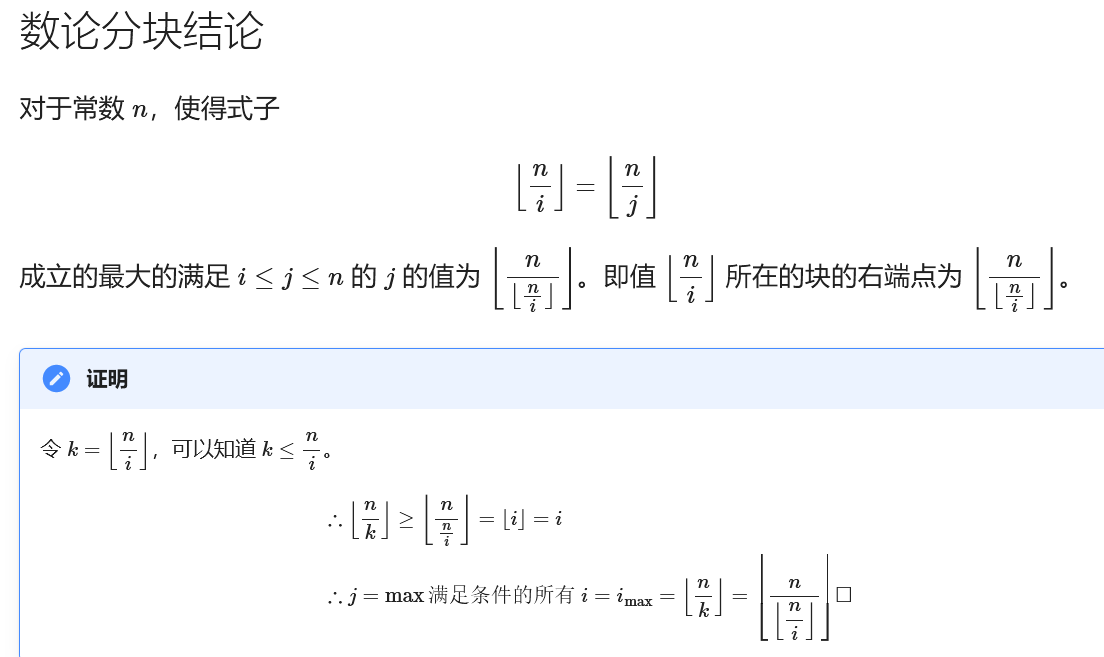
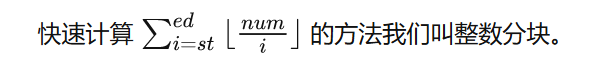
int block(int l, int r, int num) {
    int ans = 0, last = 0;
    r = min(r, num);
    for (int i = l; i <= r; i = last + 1) {
        last = min(r, num / (num / i));
        ans += (last - i + 1)*(num / i);
    }
    return ans;
}

 __int128 模板

最大值为 (2 ^127) - 1

__int128 read() {
    __int128 ans = 0;
    string str; cin >> str;

    for(int i = 0; i < str.size(); i ++) {
        ans = ans * 10 + str[i] - '0';
    }

    return ans;
}

void print(__int128 x) {
    if(x > 9) print(x / 10);
    putchar(x % 10 + '0');
}