2021.4.30

吐了 这t1啥破玩意 纯adhoc 爬
t2原题
t3挺好玩的，回头补（CFgym102987C）
首先把题意中的式子转化为从\((0,0)\)走到\((B,R)\)，所有路径上的点，和\((0,0)\)，\((B,R)\)的斜率最小值之和。

考虑枚举这个斜率最小值\(A\)，那么问题就变成了所有路径经过\(y=Ax\)和\(y-R=A(x-B)\)之间的点个数之和。

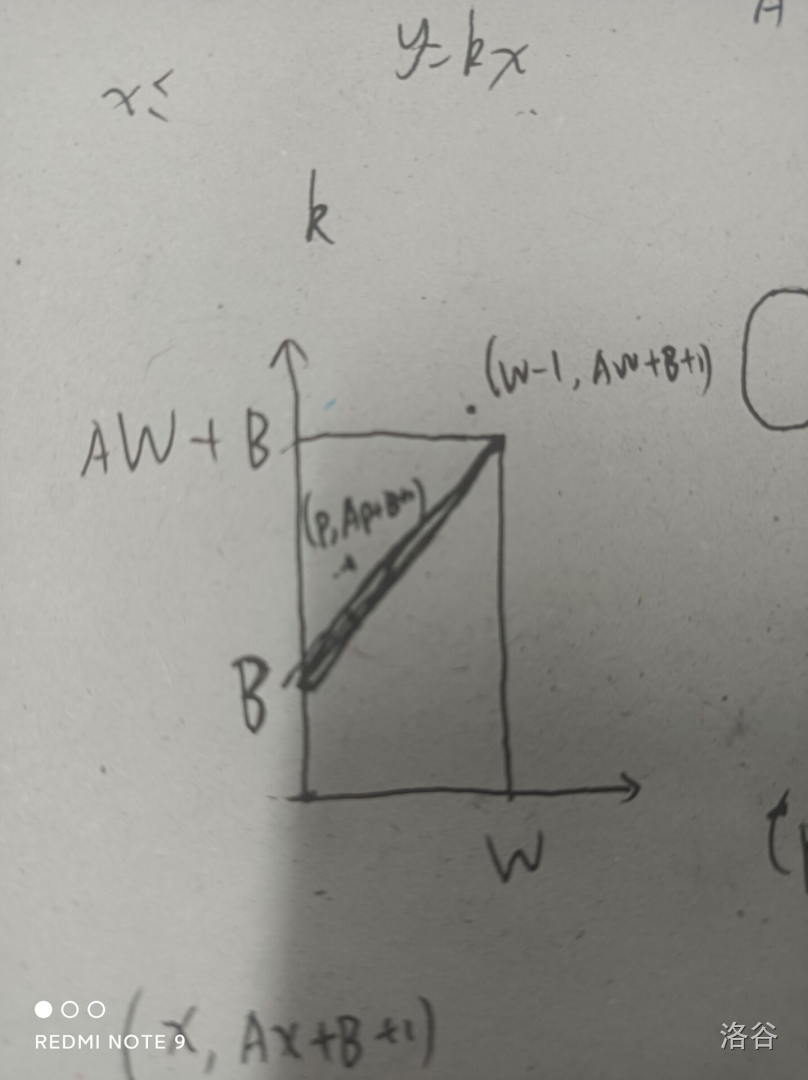
设\(f(W,A,B)\)为从\((0,0)\)出发，不穿过直线\(y=Ax+B\)，走到\((W,AW+B)\)的路径条数

枚举第一次穿过直线的横坐标\(p\)，有

\[f(W,A,B)=C(AW+B+W,W)-\sum\limits_{p=0}^{W-1}f(p,A,B)C(AW-Ap+W-p-1,W-p) \]

再考虑任意从\((0,0)\)出发，走到\((W-1,AW+B+1)\)的路径，枚举他第一穿过直线的横坐标\(p\)，有

\[C(AW+B+W,W-1)=\sum\limits_{p=0}^{W-1}f(p,A,B)C(AW-Ap+W-p-1,W-p-1) \]

\[\sum\limits_{p=0}^{W-1}f(p,A,B)C(AW-Ap+W-p-1,W-p)=A\times C(AW+B+W,W-1) \]

那么\(f(W,A,B)=C(AW+B+W,W)-A\times C(AW+B+W,W-1)\)

那个两条直线之间的区域可以看做\((R-AB+1)\)条斜率为\(A\)的直线。那么只需计算所有路径经过一条直线\(y=Ax+B\)的次数即可。

设其为\(g(W,H,A,B)\)，发现这东西枚举每一个点的贡献之后后面的式子和\(f\)很像，就考虑计算

\[g(W,H,A,B)-A\times g(W-1,H+1,A,B)=\sum\limits_{p=0}^WC(Ap+B+p,p)\times(C(W+H-B-p-Ap,W-p)-A\times C(W+H-B-p-Ap,W-p-1)) \]

\[=\sum\limits_{p=0}^WC(Ap+B+p,p)f(w-p,A,H-AW-B) \]

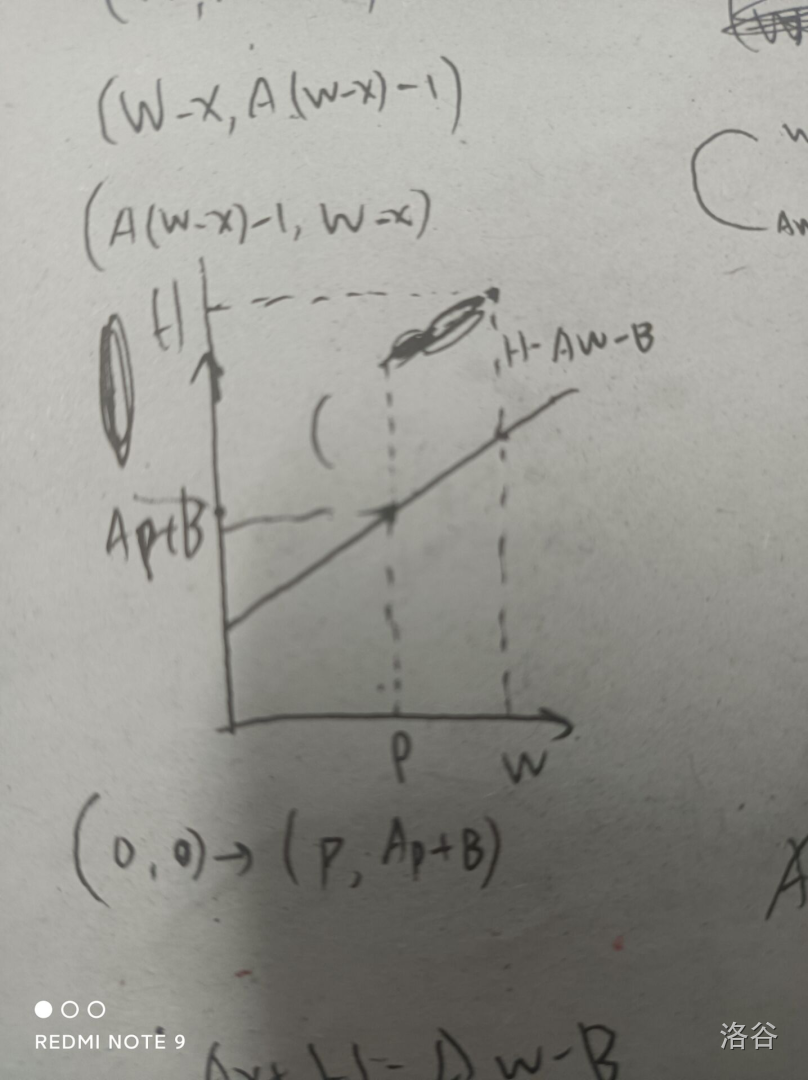
考虑这东西的意义是对于每个在直线上的点，首先无限制走到他，然后不穿过直线下方走到\((W,H)\)的路径条数。因为后面其实相当于把原始定义的图给翻转了一下。

然后考虑你每条路径多走一步向上，那就变成了最后一步向上走，走到\((W,H+1)\)的路径条数，再把这步移到\((p,Ap+B)\)之后，那么就变成了从\((0,0)\)走到\((W,H+1)\)的任意路径，\(p\)钦定的是最后一次经过直线。头一次见这么变态的组合意义。

那么就有\(g(W,H,A,B)=C(W+H+1,W)+A\times g(W-1,H+1,A,B)\)，推一推可得

\[g(W,H,A,B)=\sum\limits_{i=0}^WC(W+H+1,i)A^{W-i} \]

你发现这玩意和\(B\)无关。。。极其丧心病狂

那么答案就可以简化为\(\sum\limits_{A=1}^{\lfloor\frac{R}{B}\rfloor}(R-AB+1)\sum\limits_{i=0}^BC(R+B+1,i)A^{B-i}\)

\[=\sum\limits_{i=0}^BC(R+B+1,i)((R+1)\sum\limits_{A=1}^{\lfloor\frac{R}{B}\rfloor}A^{B-i}-B\sum\limits_{A=1}^{\lfloor\frac{R}{B}\rfloor}A^{B-i+1}) \]

后面就自然数幂和即可。