交互信息量
信源的信息熵解决了定量估算信源每发出一个符号提供的平均信息量这个信源的核心问题,对于由信源、信道和信宿组成的通信系统来说,最根本的问题,还在于如何定量估算信宿收到消息后,从消息中获取多少信息的问题,也就是信息传输问题。
信道的数学模型
考虑最简单的信道,单符号离散信道,输入端允许输出\(r\)中不同的符号,输出端相应输出\(s\)中不同的符号,如下图所示
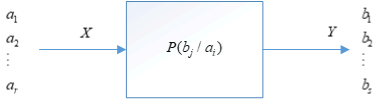
\(p(b_j/a_i)\)这个条件概率体现了信道对输入符号\(a_i\)的传递作用。不同的信道有不同的条件概率,因此条件概率\(p(b_j/a_i)\)可以称为信道的传递概率。
我们可以使用传递概率矩阵来表示信道的传递特性
\[\begin{array}{l}
\qquad \qquad \quad {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {b_1}\qquad \qquad {b_2}\qquad \ldots \qquad \quad {b_s}\\\\
[P] = \begin{array}{*{20}{c}}
{{a_1}}\\\\
{{a_2}}\\\\
\vdots \\\\
{{a_r}}
\end{array}\left( {\begin{array}{*{20}{c}}
{p({b_1}/{a_1})}&{p({b_2}/{a_1})}& \ldots &{p({b_s}/{a_1})}\\\\
{p({b_1}/{a_2})}&{p({b_2}/{a_2})}& \ldots &{p({b_s}/{a_2})}\\\\
\vdots & \vdots & \ldots & \vdots \\\\
{p({b_1}/{a_r})}&{p({b_2}/{a_r})}& \ldots &{p({b_s}/{a_r})}
\end{array}} \right)
\end{array}
\]
交互信息量
怎么计算两个事件之间传递的信息量,或者说怎么计算信宿接收到的信息量,我们可以这么理解,我们把对不确定性大小的消除理解为接收到的信息量,消除了多少不确定性就代表接收到了多少的信息。那么消除的不确定的表达式是什么呢?应该是信宿在接收前对信源发出符号的不确定性减去在接收到符号后对信源还保留的不确定性的大小。那么我们就可以定义交互信息量了,简称互信息。
互信息表示的两个事件之间传递的信息量,我们定义为
\[I(x;y) = I(x) - I(x|y)
\]
上面的定义可以这么理解:对于一个通信系统,\(I(x)\)表示接收到\(x\)前,信宿对信源发送\(x\)的不确定性,\(I(x|y)\)表示接收到符号后,推测发送的是\(x\)的还保留的不确定性,二者之差就表示信宿消除的不确定性,也就表示信宿所获得的信息量。
根据上面的表达式,我们可以推出\(I(x;y)\)的表达式为
\[I(x;y) = I(x) - I(x|y)= -logP(x) + logP(x|y) = log\cfrac{P(x|y)}{p(x)} = log\cfrac{p(x,y)}{p(x)p(y)} = I(x) + I(y) - I(xy)
\]
从另一个角度理解\(I(x|y)\)
\[I(x;y) = I(x) - I(x|y)
\]
\(I(x;y)\)表示信宿获得的信息量,\(I(x)\)表示发送方发送的信息量,那么$I(x|y)= I(x) - I(x;y) $就可以看做是在符号传输过程中损失的信息量。
反向信道
在已知先验概率\(p(a_i)\)以及信道传递概率\(p(b_j/a_i)\)的情况下,我们可以很简单的计算出后验概率\(p(a_i/b_j)\)
\[p(a_i/b_j) = \cfrac{p(a_ib_j)}{\sum\limits_{i=1}^{r}p(a_i)p(b_j/a_i)} = \cfrac{p(a_i)p(b_j/a_i)}{\sum\limits_{i=1}^{r}p(a_i)p(b_j/a_i)}
\]
那么\(p(a_i/b_j)\)可以看做是信源是\(Y\),信宿为\(X\)的传递概率,相应的信道我们称之为反向信道,相应的反向信道传递概率矩阵为
\[\begin{array}{l}
\qquad \qquad \quad {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {a_1}\qquad \qquad {a_2}\qquad \ldots \qquad \quad {a_r}\\
[P] = \begin{array}{*{20}{c}}
{{b_1}}\\\\
{{b_2}}\\\\
\vdots \\\\
{{b_s}}
\end{array}\left( {\begin{array}{*{20}{c}}
{p({a_1}/{b_1})}&{p({a_2}/{b_1})}& \ldots &{p({a_r}/{b_1})}\\\\
{p({a_1}/{b_2})}&{p({a_2}/{b_2})}& \ldots &{p({a_r}/{b_2})}\\\\
\vdots & \vdots & \ldots & \vdots \\\\
{p({a_1}/{b_s})}&{p({a_2}/{b_s})}& \ldots &{p({a_r}/{b_s})}
\end{array}} \right)
\end{array}
\]
那么
\[I(y;x) = I(y) - I(y|x) = -logP(y) + logP(y|x) = log\cfrac{P(y|x)}{p(y)} = log\cfrac{p(x,y)}{p(y)p(x)} = I(x) + I(y) - I(xy)
\]
我们可以得到
\[I(x;y) = I(y;x)
\]
所以不论是\(X\)向\(Y\)传递信息,还是\(Y\)向\(X\)传递信息,它们传递的信息量是相同的,这也是它们为什么叫做互信息的原因。
条件互信息量
考虑三个事件\(x,y,z\),条件互信息量即在其中一个事件发生的情况下,另外两个事件所交互的信息量,根据互信息量的定义,条件互信息量应定义为
\[I(x;y|z) = I(x|z) - I(x|yz)
\]
我们可以得到条件互信息量的表达式
\[I(x;y|z) = \log{}\cfrac{p(x|yz)}{p(x|z)} =\log{}\cfrac{p(x,y|z)}{p(x|z)p(y|z)} = I(x|z) + I(y|z) - I(xy|z)
\]
同理,我们可以得到
\[I(x;y|z) = I(y;x|z)
\]
平均交互信息量
如何计算信源\(X\)向信宿\(Y\)传递的信息的大小,或者说怎么计算信宿接收到信息的大小。同上,我们把信宿\(Y\)接收到的信息大小也定义为对信源\(X\)不确定性的消除。那么同理我们可以很快的得出交互信息量的表达式
\[I(X;Y) = H(X) - H(X/Y) = H(X) + H(Y) - H(XY)
\]
所表达的意思同上。
同样的我们可以得到
\[I(Y;X) = H(Y) - H(Y/X) = H(X) + H(Y) - H(XY)
\]
所以我们得到
\[I(X;Y) = I(Y;X)
\]
平均互信息量的性质
非负性
考虑
\[I(X;Y) = \sum_{i = 1}^r\sum_{j = 1}^sp(a_ib_j)\log{}\cfrac{p(a_ib_j)}{p(a_i)p(b_j)}
\]
则
\[\begin{aligned}
-I(X;Y) &= \sum_{i = 1}^r\sum_{j = 1}^sp(a_ib_j)\log{}\cfrac{p(a_i)p(b_j)}{p(a_ib_j)} \\\\
&\leq \log{}\sum_{i = 1}^r\sum_{j = 1}^sp(a_ib_j)\cfrac{p(a_i)p(b_j)}{p(a_ib_j)} \\\\
&= \log{} 1 \\\\
&= 0
\end{aligned}
\]
所以
\[I(X;Y) \geq 0
\]
上面利用了\(\log\)函数是上凸函数的性质,即
\[\log{}\sum_{i=1}^n p_ix_i \geq \sum_{i=1}^n p_i\log{}x_i
\]
其中
\[\sum_{i=1}^np_i = 1
\]
当前仅当两个随机变量\(X,Y\)统计独立时,才有\(I(X;Y)=0\)。
极值性
我们知道,互信息量的表达式为
\[\begin{aligned}
I(X;Y) &= H(X) - H(X|Y) \\
&= H(Y) - H(Y|X)
\end{aligned}
\]
并且
\[H(X|Y) = \sum_{i = 1}^r\sum_{j = 1}^s p(a_ib_j)\log{}\cfrac{1}{p(a_i|b_j)} \\
\]
由于\(0\leq p(a_ib_j)\leq 1, 0\leq p(a_i|b_j) \leq 1\),所以
\[p(a_ib_j)\log{}\cfrac{1}{p(a_i|b_j)} \geq 0
\]
所以我们得到
\[H(X|Y) \geq 0
\]
同理,我们也可以得到
\[H(Y|X) \geq 0
\]
所以有
\[I(X;Y) = H(X) - H(X|Y) \leq H(X) \\
I(Y;X) = H(Y) - H(Y|X) \leq H(Y)
\]
这表示\(I(X;Y)\)有最大值,是为极值性。
那么在什么条件下取得极值呢? 首先看
\[I(X;Y) = H(X) - H(X|Y)
\]
明显,当\(H(X|Y) = 0\)时,\(I(X;Y)\)可以取得极大值\(H(X)\),所以\(H(X|Y)\)在什么条件下取值为\(0\)呢? 要回答这个问题,可以从\(H(X|Y)\)的物理意义出发,\(H(X|Y)\)表示信宿接收到符号后,对信源发送什么符号的猜测,表示猜测的不确定性的大小,如果\(H(X|Y)\)为\(0\)则表示,对信源发出符号不确定性为\(0\),即可以完美的知道信源发出的符号是什么,所以信道模型应该如下
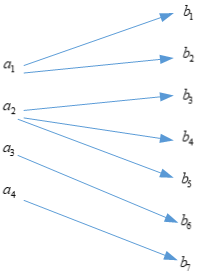
这样的话,当接收到符号后,可以推测出信源发出的是什么,相应的信道转移概率矩阵为
\[\begin{array}{*{20}{l}}
{\quad \quad \quad \qquad \quad {b_1}\qquad \quad {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {b_2}\qquad \qquad {b_3}\qquad \qquad {b_4}\qquad \qquad {b_5}\qquad \qquad {b_6}\qquad \qquad {b_7}}\\\\
{[P] = \begin{array}{*{20}{c}}
{{a_1}}\\\\
{{a_2}}\\\\
{{a_3}}\\\\
{{a_4}}
\end{array}\left( {\begin{array}{*{20}{c}}
{p({b_1}/{a_1})}&{p({b_2}/{a_1})}&0&0&0&0&0\\\\
0&0&{p({b_3}/{a_2})}&{p({b_4}/{a_2})}&{p({b_5}/{a_2})}&0&0\\\\
0&0&0&0&0&{p({b_6}/{a_3})}&0\\\\
0&0&0&0&0&0&{p({b_7}/{a_4})}
\end{array}} \right)}
\end{array}
\]
我们观察,可以发现每一列只有一个非零值。所以我们可以得到这么一个结论,当转移概率矩阵的每一列只有一个非零值,\(I(X;Y)\)可以取到最大值为\(H(X)\)。
同理,当\(H(Y|X)\)为\(0\)时,应该有如下的信道模型
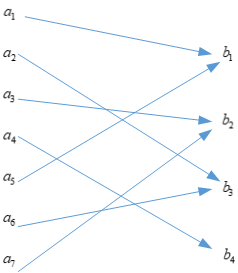
对应的信道转移概率矩阵为
\[\begin{array}{l}
\qquad \quad \quad\,\,{\mkern 1mu} {\mkern 1mu} {b_1}\,\,\,\, {b_2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}\,\, {b_3}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}\, {b_4}\\\\
P = \begin{array}{*{20}{c}}
{{a_1}}\\\\
{{a_2}}\\\\
{{a_3}}\\\\
{{a_4}}\\\\
{{a_5}}\\\\
{{a_6}}\\\\
{{a_7}}
\end{array}\left( {\begin{array}{*{20}{c}}
1&0&0&0\\\\
0&0&1&0\\\\
0&1&0&0\\\\
0&0&0&1\\\\
1&0&0&0\\\\
0&0&1&0\\\\
0&1&0&0
\end{array}} \right)
\end{array}
\]
观察该信道转移概率矩阵的特点,该矩阵只由\(0\)和\(1\)组成,所以我们可以得到这个结论,当转移概率矩阵中所有元素,要么是\(0\),要么为\(1\)时,则\(I(X;Y)\)取得最大值,最大值为\(H(Y)\)。
考虑这么一种特殊情形,是上面两种情况的结合,即信道转移概率矩阵的每一列只有一个非零元素,并且该矩阵只由\(0\)和\(1\)组成,那么我们可以得到转移概率矩阵为
\[P = \left( {\begin{array}{*{20}{c}}
0&1&0&0&0\\\\
1&0&0&0&0\\\\
0&0&0&1&0\\\\
0&0&0&0&1\\\\
0&0&1&0&0
\end{array}} \right)
\]
对应的信道模型为
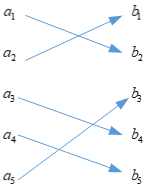
此时信道模型是一一对应的,并且此时\(I(X;Y)\)取得最大值为\(H(X) = H(Y)\)。
不增性
在实际通信系统中,常需要对信道传输的数据作适当处理。若把数据处理装置亦看做是一个信道,这就由两个信道串接,组成了一个串联信道:

则
\[I(X;Z) \leq I(X;Y)
\]
具体的证明可以查阅书本,这里只讲表示的意义,\(I(X;Z)\)表示\(Z\)获得信息量,\(I(X;Y)\)表示\(Y\)获得的信息量,上面的关系式表示,在经过信道\(II\)后,即经过数据处理后(不论怎么处理),信息都有所损失,这就是数据处理定理。即不论怎么处理数据,最好的情况是没有信息的损失,但是一定不会有信息的增加。
上式取等号当且仅当信道\(II\)是一个可逆信道时,即\(Z\)经过信道\(II\)的可逆信道后,可以完整的将\(Y\)恢复出来,这时等号成立:
\[I(X;Z) = I(Y;Z)
\]
上凸性
互信息量的表达式为
\[\begin{aligned}
I(X;Y) &= \sum_{i = 1}^{r}\sum_{j = 1}^{s}p(a_{i}b_{j})\log{}\cfrac{p(b_j/a_i)}{p(b_j)} \\\\
&= \sum_{i = 1}^{r}\sum_{j = 1}^{s}p(a_{i})p(b_j/a_i)\log{}\cfrac{p(b_j/a_i)}{\sum\limits_{i=1}^rp(a_i)p(b_j/a_i)} \\\\
&= I(p(a_i),p(b_j/a_i))
\end{aligned}
\]
可以发现,互信息量是先验概率和转移概率的函数。
当信道转移概率\(p(b_j/a_i)\)确定时,此时\(I(X;Y)\)是关于\(p(a_i)\)的函数,在数学上可以证明,\(I(p(a_i))\)是上凸函数,即存在最大值。所以当信道转移概率确定时,即在给定信道的条件下,存在一种信源分布,使得\(I(X;Y)\)最大,这个值是对给定信道的情况下最多能够传输的信息量,所以我们定义这个量为信道容量\(C\),即
\[C = max\{I(X;Y)\}
\]
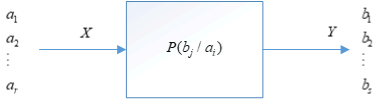





 浙公网安备 33010602011771号
浙公网安备 33010602011771号