圆方树 Round-Square Tree

更新日志

2025/07/03：开工。

---

前言

众所周知的，圆方树分为狭义圆方树与广义圆方树两种，前者使用边双实现，而后者使用点双实现。

前者一般用于仙人掌图，而后者可以用于一般图且兼容仙人掌图问题，因此这里讲解广义圆方树。

思路

首先你需要会找点双联通分量。这个链接比较古早，有些稚嫩，或者自行上网搜索吧。

圆方树其实也就是对每个点双联通分量开一个新点，然后断开原图所有边，将每个分量对应点与其分量内的各点连边。令原点为圆点，新点为方点，不难发现只存在连接圆点与方点的边。借图 OI-wiki 一张：

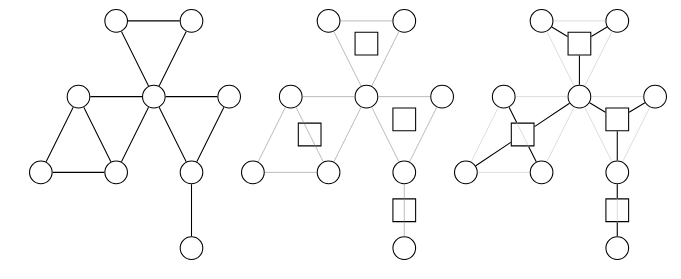
我们在找点双的时候顺便在新图上连边即可。

其实多数圆方树的题目的重点在于这个新边的边权是什么，这个需要视题目需求考虑。后文有对例题的讲解，可以感受一下。

点分数量显然不超过原点数，因此新图点数是 \(2n\) 级别的。

模板

这里模板就不设边权了。\(nn\) 记得初始化为 \(n\)。

int n,m,nn;
vec<int> g[N];

int dcnt;
int dfn[N],low[N];
stack<int> stk;
vec<int> G[N<<1];
void tarjan(int now,int fid){
    dfn[now]=low[now]=++dcnt;
    stk.push(now);
    for(auto e:g[now]){
        int nxt=e.fir,val=e.sec;
        if(nxt==fid)continue;
        if(!dfn[nxt]){
            dis[nxt]=dis[now]+val;
            tarjan(nxt,now);
            chmin(low[now],low[nxt]);
            if(low[nxt]>=dfn[now]){
                ++nn;
                while(1){
                    int tp=stk.top();stk.pop();
                    G[nn].pub(tp);G[tp].pub(nn);
                    if(tp==nxt)break;
                }
                G[nn].pub(now);G[now].pub(nn);
            }
        }else chmin(low[now],dfn[nxt]);
    }
}

例题

P5236 【模板】静态仙人掌
考虑新边的边权，令一个点双内 \(dfn\) 最小的点为这个点双的根，则边权就是这个点到这个点双的根的最小距离。

我们在 tarjan 的时候顺便记录 \(dis\)，那么最小距离要么是 \(dis\)，要么是环长减去 \(dis\)。

至于环长怎么求，仙人掌中一条边只用于一个环，那么一个点只会有一条返祖边，把这条返祖边记下来即可。注意判断是返祖边还是双向向子节点连的边，也就是判断一下 \(dfn\) 的大小，不然 5pts。

然后我们对于生成的圆方树跑倍增 LCA 即可。我们预处理出距离前缀和（注意与之前求得的 \(dis\) 区分，\(dis\) 还有用）和倍增父节点信息即可。

如果二点的 LCA 为圆点，那么答案就正常差分距离求一下即可。否则，我们需要找出 LCA 对应环上两个点的最近距离。我们在 tarjan 的时候不是记录了 \(dis\) 吗，由于是 DFS 出的，环内 \(dis\) 其实就是某个方向的边权前缀和，两点的 \(dis\) 差或者环长减去两点的 \(dis\) 差就是答案，取个 \(\min\) 即可。

code

const int N=1e4+5,T=16;

int n,m,q,nn;
vec<pii> g[N];

int dcnt;
int dfn[N],low[N];
stack<int> stk;
vec<pii> G[N<<1];
int len[N<<1];
int dis[N],rec[N];
void tarjan(int now,int fid){
    dfn[now]=low[now]=++dcnt;
    stk.push(now);
    for(auto e:g[now]){
        int nxt=e.fir,val=e.sec;
        if(nxt==fid)continue;
        if(!dfn[nxt]){
            dis[nxt]=dis[now]+val;
            tarjan(nxt,now);
            chmin(low[now],low[nxt]);
            if(low[nxt]>=dfn[now]){
                ++nn;
                while(1){
                    int tp=stk.top();stk.pop();
                    G[nn].pub({tp,dis[tp]-dis[now]});
                    chmax(len[nn],dis[tp]-dis[now]+rec[tp]);
                    if(tp==nxt)break;
                }
                G[nn].pub({now,0});
                if(G[nn].size()==2)len[nn]=val*2;
                for(auto &e:G[nn])chmin(e.sec,len[nn]-e.sec),G[e.fir].pub({nn,e.sec});
            }
        }else if(dfn[nxt]<dfn[now])chmin(low[now],dfn[nxt]),rec[now]=val;
    }
}

int fa[N<<1][T];
int dp[N<<1],dist[N<<1];
void dfs(int now,int fid){
    fa[now][0]=fid;
    for(auto e:G[now]){
        int nxt=e.fir,val=e.sec;
        if(nxt==fid)continue;
        dp[nxt]=dp[now]+1;
        dist[nxt]=dist[now]+val;
        dfs(nxt,now);
    }
}
int getdis(int a,int b){
    if(dp[a]>dp[b])swap(a,b);
    int c=b;
    per(t,T-1,0)if(dp[fa[c][t]]>=dp[a])c=fa[c][t];
    if(a==c)return dist[b]-dist[a];
    int d=a;
    per(t,T-1,0)if(fa[c][t]!=fa[d][t])c=fa[c][t],d=fa[d][t];
    if(fa[c][0]<=n){
        c=fa[c][0];
        return dist[a]-dist[c]+dist[b]-dist[c];
    }else{
        int e=fa[c][0];
        return dist[a]-dist[d]+dist[b]-dist[c]+min(abs(dis[c]-dis[d]),len[e]-abs(dis[c]-dis[d]));
    }
}

inline void Main(){
    read(n,m,q);
    rep(i,1,m){
        int u,v,w;read(u,v,w);
        g[u].pub({v,w});g[v].pub({u,w});
    }
    nn=n;tarjan(1,0);
    dfs(1,1);
    repl(t,1,T)rep(i,1,nn)fa[i][t]=fa[fa[i][t-1]][t-1];
    while(q--){
        int u,v;read(u,v);
        put(getdis(u,v));
    }
}