「AGC004F-Namori」题解

F - Namori

sol

前言

神仙题啊。

操作转换

考虑原操作过于繁琐，难以操作。

有一个经典但神奇的转化：对于一个二分图，这个操作等价于，将图黑白相间染色后，交换相邻两个点的颜色。最后的状态与初始的状态完全相反（白变黑黑变白）时等价于本题中所有颜色变黑时。

感觉很典，但我并不知道，是我菜了。

然后这个问题就简单多了。

树

下文所有颜色均指上文操作转换后新图的颜色。

下面就开始考验人类智慧了。

考虑拆贡献，把总操作次数拆到各边上，分别统计各边的贡献。这就比较反直觉了，但我们暂时还无法证明。

考虑一条边至少需要操作几次，考虑其下方的子树，既然要使得子树内黑白点互换位置，就要使得它们互换数量。因此一条边至少要被交换黑白点个数差次。

然后我们发现这个其实就是答案。

一棵子树的黑白节点差，其实就来自于其根节点与其各下层子树内部的黑白节点差，因此各个子树内部实际上是独立的，我们只需要考虑子树根节点位置的变化即可，并且各级子树的需求是有关联的，上层子树的差必然由下层子树及根节点转移来，这样我们必然可以构造出一种方案使得不存在多余的操作，每次恰好和某子树交换所需要的，恰好和上一层交换所需要的。

记以 \(i\) 节点为根的子树内黑节点数减去白节点数为 \(a_i\)，最后答案即为 \(\sum|a_i|\)。对 \(a\) 的转移是简单的。

倘若根节点 \(a_{rt}\) 非零则无解，因为它没有父边供交换了。

基偶环树

考虑把环单独来看，分别对环上每个点在以其为根的子树上跑一遍上述 DP，那么我们现在需要考虑各个根节点之间的转移。

记环上第 \(i\) 点为根的子树得到的值为 \(v_i\)，第 \(i\) 条边上的转移系数为 \(x_i\)，\(x_i\) 的正负表示方向而大小表示转移量。

画个图：

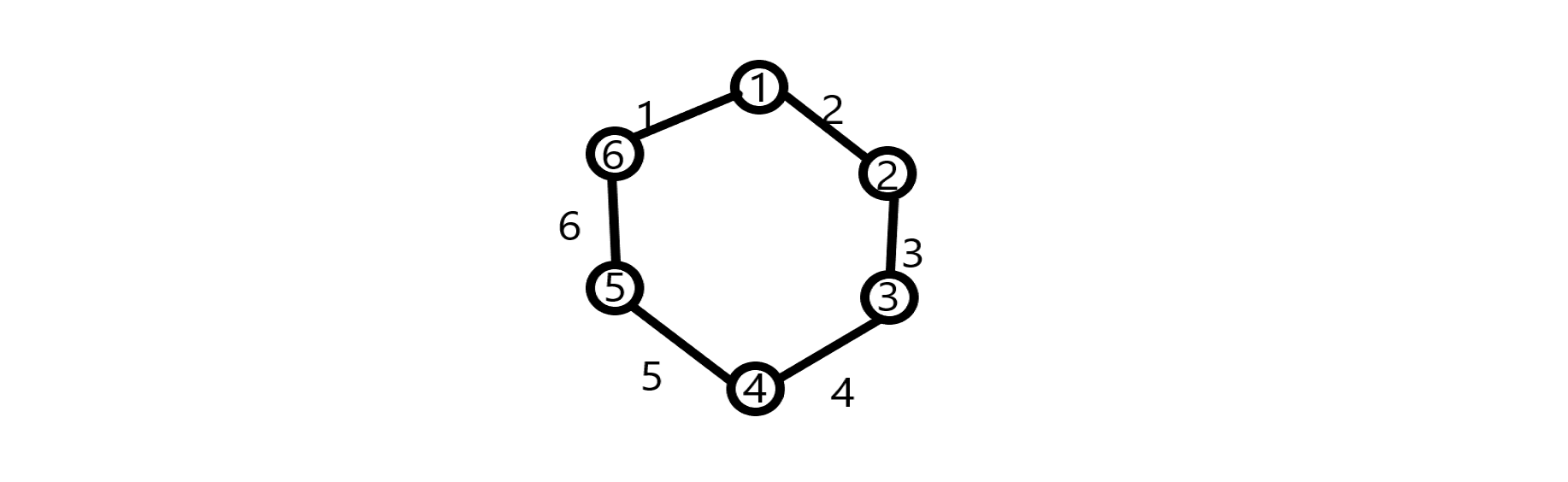
由于最后整个基环树是平衡的，因此我们可以用一条边边权表示出其余所有边。具体的：

\[x_{i+1}=x_i+v_i \]

那么：

\[\begin{align*} &x_1=x_1\\ &x_2=x_1-v_1\\ &x_3=x_2-v_2\\ \vdots\\ &x_n=x_{n-1}-v_{n-1} \end{align*} \]

转化得：

\[\begin{align*} &x_1=x_1-0\\ &x_2=x_1-v_1\\ &x_3=x_1-v_1-v_2\\ \vdots\\ &x_n=x_1-\sum_{i=1}^{n-1}v_i \end{align*} \]

发现问题变为给出区间一些点，找到一个最优点使得这个点到其余所有给出点的距离之和最小。

这就是个小学问题，找中位数位置即可。

考虑后面的所有前缀和形式，如果我们断开上图中的边 \(1\) 并从点 \(6\) 开始跑在树上的那个 DP，那么不难发现点 \(1\) 到点 \(5\) 的 \(a\) 值就是我们所需要的前缀和，同时根节点的 \(a\) 恰好为 \(0\)，于是我们把环上所有值跑出来即可得到需要的 \(x_1\)。

至于为什么根节点 \(a\) 值必须恰好为 \(0\)，因为偶环的那条边并不能改变什么，只能优化一些转移，因此根节点的需求仍然无从满足。

然后环上所有边的边权就需要变为 \(x_1\) 减去其原先的 \(a\) 值，实际上由于最后会取绝对值所以直接减去 \(x_1\) 即可。

基奇环树

奇环上一条边的作用，其实是同时改变其两边点的颜色，也就是说，这条边可以改变答案。

不难发现这条边只能支持两两抵消，所以根节点的需求为奇数则无解。

否则这条边将会操作 \(|\frac{a_{rt}}{2}|\) 次。同时，它使得环内各边的 \(a\) 发生了变化，因此各边的 \(a\) 均需减去 \(\frac{a_rt}{2}\)，注意这里的 \(a_{rt}\) 是带符号的。

于是这道题就结束了。

code

const int N=1e5+5;

int n,m;
int rt=1,hn;

struct DSU{
    int fa[N];
    inline void init(){rep(i,1,n)fa[i]=i;}
    inline int find(int x){if(fa[x]!=x)fa[x]=find(fa[x]);return fa[x];}
    inline void merge(int a,int b){fa[find(a)]=find(b);}
    inline bool same(int a,int b){return find(a)==find(b);}
}dsu;

vec<int> g[N];

int f[N],fa[N];
void solve(int now,int fid,int kd=1){
    f[now]=kd;fa[now]=fid;
    for(auto nxt:g[now])if(nxt!=fid)solve(nxt,now,-kd),f[now]+=f[nxt];
}

inline void Main(){
    read(n,m);
    dsu.init();
    rep(i,1,m){
        int a,b;read(a,b);
        if(dsu.same(a,b)){
            rt=a;hn=b;
            continue;
        }
        dsu.merge(a,b);
        g[a].pub(b);g[b].pub(a);
    }
    solve(rt,0);
    if(n==m){
        int len=0;for(int i=hn;i;i=fa[i])++len;
        if(len&1){
            if(f[rt]&1)return put(-1);
            for(int i=hn;i;i=fa[i])f[i]-=f[rt]>>1;
        }else{
            if(f[rt])return put(-1);
            vec<int> v(1);
            for(int i=hn;i;i=fa[i])v.pub(f[i]);
            sort(v.begin(),v.end());
            f[rt]=v[len>>1];
            for(int i=hn;i!=rt;i=fa[i])f[i]-=f[rt];
        }
    }else if(f[rt])return put(-1);
    int ans=0;
    rep(i,1,n)ans+=abs(f[i]);
    put(ans);
}