Graham 算法维护二维凸包

更新日志

2025/05/25：开工。

---

思路

二维凸包。这里讲解 Graham 算法，因为它只用扫一遍，相对方便一些。

这个算法的大致思路就是，从一个点开始，每次找下一个短期可行点加入凸包并删除此前已在凸包中的不合法点，最后就可以得到一个完整的凸包。

看不懂也很正常，我自己光看这一句也不懂后面对其进行细致讲解。

首先解释一下短期可行的概念吧，如果不考虑后面的点，那么这个点必然可以加入凸包，这就是短期可行。

而短期可行的概念是相对的，需要有一个参照物也就是起点，假如起点错误，那么算法就错了，因此我们需要确定一个绝对可行的点作为整个算法的起点。换句话说，也就是找到一个必然在凸包上的点作为算法的起点。

第一步，确定起点。不难想到找一个“边上”的点即可。例如，我们找最左下角的点，以纵坐标为第一关键字、横坐标为第二关键字升序排序之后的第一个点（交换关键字顺序也没关系，都在边上不是么）。这个点必然是位于最后的凸包上的。

第二步，排序剩余点。我们需要保证接下来的每一步都短期可行，考虑以起点为极点将其余点按极角排序，这样我们依次加入点的话，当前点存在于凸包中可以将之前的所有点都囊括起来，也就是一个短期可行情况。换句话说，只考虑到这一步，这个点必然存在于凸包中，满足局部最优。

特殊地，对于极角相同的情况，我们把距离更近的排在前面。对于共线的情况，由于误差的存在，如果我们乱序处理这些点的话，可能会错误地将最外侧的点弹出。

第三步，依次加入凸包。既然我们已经确定当前点短期可行即局部最优，那么之前一些与当前点发生冲突的短期可行点就不合法了。单纯靠语言说清楚冲突是什么很困难，所以我们上一张图：

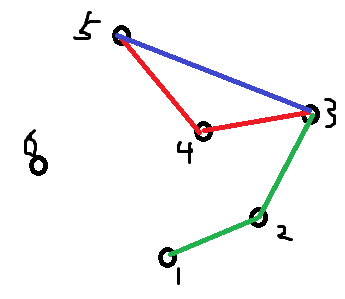
所有点均已按顺序标号，当前考虑到点五，绿边表示已确定的边，红边表示发生冲突的边，蓝边表示解决冲突后应有的边。

通过这张图或许也能更好地感受一下短期可行的含义。

然后我们说一下冲突的具体含义，假如我们是这样逆时针处理凸包的，而上一条边与最新一条边发生顺时针方向的偏转，就不合法了。我们可以通过叉乘完成这个判断。

这样用单调栈处理完所有点就行了。你无需在最后用起点再去判断最后几个点是否合法，因为最后一个点满足短期可行，也就是如果它之后没有别的点的话能构成一个合法凸包，它之后确实也没有别的点了，因此它必然可行。

直接放模板题吧。

例题

Fencing the Cows

code

const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;

const int N=1e5+5;

struct point{ld x,y;};
ld cross(point a,point b){return a.x*b.y-b.x*a.y;}
ld dist(point a,point b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}

int n;
point ps[N];
point stk[N];int top;

int main(){
	read(n);
	rep(i,1,n)readf(ps[i].x),readf(ps[i].y);
	int chs=1;
	rep(i,2,n)if(ps[i].y<ps[chs].y||ps[i].y==ps[chs].y&&ps[i].x<ps[chs].x)chs=i;
	swap(ps[1],ps[chs]);sort(ps+2,ps+1+n,[&](point a,point b){
		ld cra=atan2(a.y-ps[1].y,a.x-ps[1].x);
		ld crb=atan2(b.y-ps[1].y,b.x-ps[1].x);
		if(cra!=crb)return cra<crb;
		else return dist(ps[1],a)<dist(ps[1],b);
	});
	stk[++top]=ps[1];
	rep(i,2,n){
		while(top>1&&cross({stk[top].x-stk[top-1].x,stk[top].y-stk[top-1].y},{ps[i].x-stk[top].x,ps[i].y-stk[top].y})<=0)--top;
		stk[++top]=ps[i];
	}
	stk[0]=stk[top];
	ld ans=0;
	rep(i,1,top)ans+=dist(stk[i-1],stk[i]);
	writef(ans);
	return 0;
}