猫树 CatTree
更新日志
2025/04/22:开工。概念
猫树,是一种广义线段树,但并不是我们通常意义上的那种线段树的实现方式。
这是一种不支持修改,\(O(n\log n)\) 建树,\(O(1)\) 查询的数据结构。
适用于 \(n,q\) 不同阶的情况。同时很适合维护区间线性基信息,最后会提一嘴这个。
实现
建树
首先,为了方便 \(O(1)\) 查询,我们先把数列补成 \(2\) 的次幂。后文中的 \(n\) 代指补完后的数列长度。
对于每一个节点,我们将其代表区间均分成左右两部分,左半部分维护从当前位到中点的后缀信息,后半部分维护从中点的后一位到当前位的后缀信息。
我们不建叶子节点,如果查询时有 \(l=r\) 的情况直接特判。这样总节点数有 \(n\) 个,维护信息数组大小是 \(n\log n\) 的。你可以对每一层只开一个数组,他们之间互不影响。
查询
首先,你找到最小的包含两个查询边界的区间。那么此时两个边界必然在中点两侧。
反证一下,不然其一个子区间会更小。
这里我们忽略长度为 \(1\) 的区间。
然后我们直接合并这个区间所在层这两个查询边界储存的信息即可。
然后我们考虑如何 \(O(1)\) 找到需要的节点。在我们补全之后,你发现,这时候两个节点的二进制表示的最长公共前缀就是所求节点。
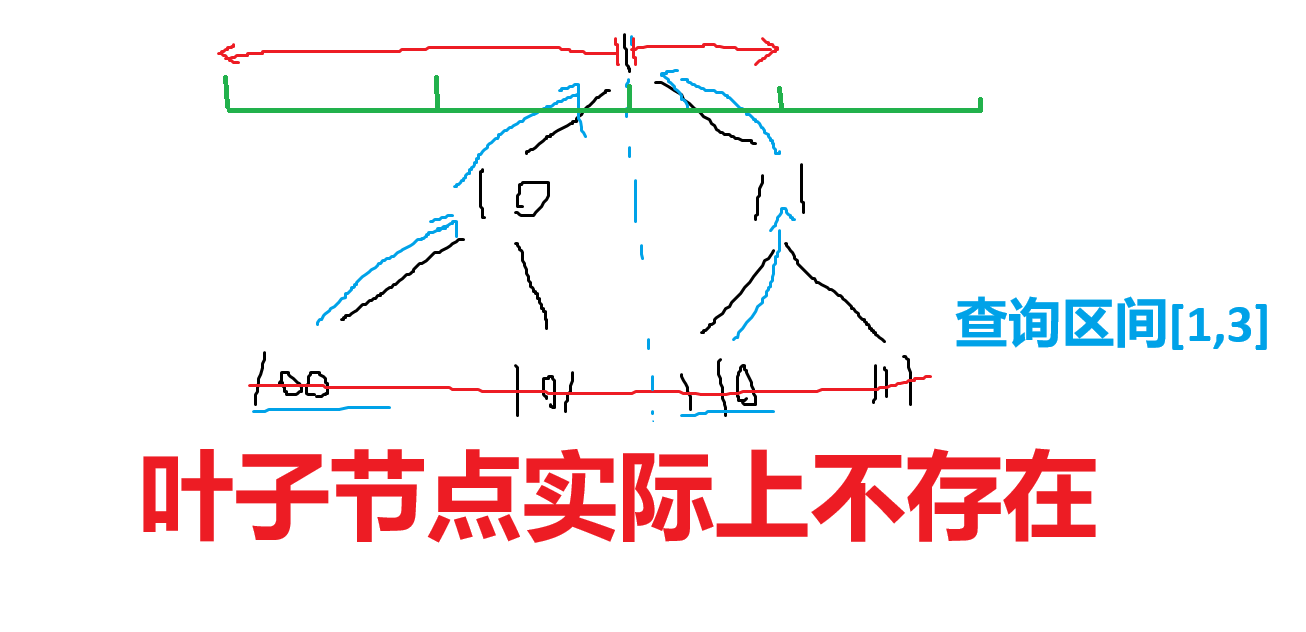
如图,\(1\) 节点就是满足要求的节点。
我们从 \(0\) 开始从上到下为层数编号,假如查询区间是 0-based 的,那么我们需要的那一层就在:
int h=lg[n-1]-lg[l^r];
之所以没有真的找叶子节点编号,是因为叶子节点的编号性质,最高位都是 \(1\) 可以忽略,剩下的其实就是下标。
然后我们就直接放例题了。
例题
题解
我们考虑维护两个信息:当前节点到中点这个区间内的最大子段和,当前节点到中点这个区间内最大的以中点为一个端点的区间的子段和。
获取答案时,我们分别获取两边各自的最大子段和,以及通过第二个信息获取区间过中点的最大子段和即可。
这两个都是很简单的贪心,可以详见代码。
然后我们讲一讲空间实现细节。
const int T=__lg((int)5e4)+1,N=1<<T;
这就是补全之后的信息。事实上,如果我们直接通过 lg[x] 来获取当前节点所在层,那么只会占用 0 ~ T-1 层,如果你不储存叶子结点的话。
如果我们使用 0-based,那么我们就可以抵着开空间:
int mxn[T][N],pre[T][N];
以及关于预处理的 lg 数组,也可以抵着开空间,因为 lg[n]-1==lg[n-1],这里和下一行 n 指补全后的序列长度。(忽略 \(1\) 的情况。)
所以我们只会用到 0 ~ n-1 的 lg 信息。
int lg[N];
抵着开数组不是好习惯,我只是说可以这么实现而已 awa
代码
猫树部分
struct catree{
int mxn[T][N],pre[T][N];
void build(int x=1,int l=0,int r=nn-1){
if(l==r)return;
int h=lg[x];
int m=l+r>>1,mxp;
mxn[h][m]=pre[h][m]=a[m];
mxp=max(0,a[m]);
per(i,m-1,l){
pre[h][i]=max(pre[h][i+1],s[m]-(i?s[i-1]:0));
mxn[h][i]=max(mxn[h][i+1],mxp+=a[i]);
chmax(mxp,0);
}
mxn[h][m+1]=pre[h][m+1]=a[m+1];
mxp=max(0,a[m+1]);
rep(i,m+2,r){
pre[h][i]=max(pre[h][i-1],s[i]-s[m]);
mxn[h][i]=max(mxn[h][i-1],mxp+=a[i]);
chmax(mxp,0);
}
build(x<<1,l,m);
build(x<<1|1,m+1,r);
}
int query(int l,int r){
if(l==r)return a[l];
int h=lg[nn-1]-lg[l^r];
return max(max(mxn[h][l],mxn[h][r]),pre[h][l]+pre[h][r]);
}
}cat;
核心代码
code
const int T=__lg((int)5e4)+1,N=1<<T;
int n,nn;
int a[N],s[N];
int lg[N];
struct catree{
int mxn[T][N],pre[T][N];
void build(int x=1,int l=0,int r=nn-1){
if(l==r)return;
int h=lg[x];
int m=l+r>>1,mxp;
mxn[h][m]=pre[h][m]=a[m];
mxp=max(0,a[m]);
per(i,m-1,l){
pre[h][i]=max(pre[h][i+1],s[m]-(i?s[i-1]:0));
mxn[h][i]=max(mxn[h][i+1],mxp+=a[i]);
chmax(mxp,0);
}
mxn[h][m+1]=pre[h][m+1]=a[m+1];
mxp=max(0,a[m+1]);
rep(i,m+2,r){
pre[h][i]=max(pre[h][i-1],s[i]-s[m]);
mxn[h][i]=max(mxn[h][i-1],mxp+=a[i]);
chmax(mxp,0);
}
build(x<<1,l,m);
build(x<<1|1,m+1,r);
}
int query(int l,int r){
if(l==r)return a[l];
int h=lg[nn-1]-lg[l^r];
return max(max(mxn[h][l],mxn[h][r]),pre[h][l]+pre[h][r]);
}
}cat;
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
repl(i,0,n)cin>>a[i],s[i]=(i?s[i-1]:0)+a[i];
rep(i,2,n)lg[i]=lg[i>>1]+1;
nn=1<<lg[n],nn<<=nn<n;
repl(i,n+1,nn)lg[i]=lg[i>>1]+1;
cat.build();
int m;cin>>m;
while(m--){
int l,r;cin>>l>>r;
cout<<cat.query(l-1,r-1)<<"\n";
}
return 0;
}
完整代码
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef __int128 i128;
typedef double db;
typedef long double ld;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef pair<int,ll> pil;
typedef pair<ll,int> pli;
template <typename Type>
using vec=vector<Type>;
template <typename Type>
using grheap=priority_queue<Type>;
template <typename Type>
using lrheap=priority_queue<Type,vector<Type>,greater<Type> >;
#define fir first
#define sec second
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define chmax(a,b) a=max(a,b)
#define chmin(a,b) a=min(a,b)
#define rep(i,x,y) for(int i=(x);i<=(y);i++)
#define per(i,x,y) for(int i=(x);i>=(y);i--)
#define repl(i,x,y) for(int i=(x);i<(y);i++)
#define file(f) freopen(#f".in","r",stdin);freopen(#f".out","w",stdout);
struct mint {
int x,mod;
inline mint(int o=0,int p=998244353) {x=o;mod=p;}
inline mint & operator=(ll o){return x=o%mod,(x+=mod)>=mod&&(x-=mod),*this;}
inline mint & operator+=(mint o){return (x+=o.x)>=mod&&(x-=mod),*this;}
inline mint & operator-=(mint o){return (x-=o.x)<0&&(x+=mod),*this;}
inline mint & operator*=(mint o){return x=(ll)x*o.x%mod,*this;}
inline mint & operator^=(ll b){mint res(1);for(;b;b>>=1,*this*=*this)if(b&1)res*=*this;return x=res.x,*this;}
inline mint & operator^=(mint o){return *this^=o.x;}
inline mint & operator/=(mint o){return *this*=(o^=(mod-2));}
inline mint & operator++(){return *this+=1;}
inline mint & operator--(){return *this-=1;}
inline mint operator++(int o){mint res=*this;return *this+=1,res;}
inline mint operator--(int o){mint res=*this;return *this-=1,res;}
friend inline mint operator+(mint a,mint b){return a+=b;}
friend inline mint operator-(mint a,mint b){return a-=b;}
friend inline mint operator*(mint a,mint b){return a*=b;}
friend inline mint operator/(mint a,mint b){return a/=b;}
friend inline mint operator^(mint a,ll b){return a^=b;}
friend inline mint operator^(mint a,mint b){return a^=b;}
friend inline bool operator<(mint a,mint b){return a.x<b.x;}
friend inline bool operator>(mint a,mint b){return a.x>b.x;}
friend inline bool operator<=(mint a,mint b){return a.x<=b.x;}
friend inline bool operator>=(mint a,mint b){return a.x>=b.x;}
friend inline bool operator==(mint a,mint b){return a.x==b.x;}
friend inline istream & operator>>(istream &in,mint &o){ll x;return in>>x,o=x,in;}
friend inline ostream & operator<<(ostream &ot,mint o){return ot<<o.x,ot;}
};
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;
const int T=__lg((int)5e4)+1,N=1<<T;
int n,nn;
int a[N],s[N];
int lg[N];
struct catree{
int mxn[T][N],pre[T][N];
void build(int x=1,int l=0,int r=nn-1){
if(l==r)return;
int h=lg[x];
int m=l+r>>1,mxp;
mxn[h][m]=pre[h][m]=a[m];
mxp=max(0,a[m]);
per(i,m-1,l){
pre[h][i]=max(pre[h][i+1],s[m]-(i?s[i-1]:0));
mxn[h][i]=max(mxn[h][i+1],mxp+=a[i]);
chmax(mxp,0);
}
mxn[h][m+1]=pre[h][m+1]=a[m+1];
mxp=max(0,a[m+1]);
rep(i,m+2,r){
pre[h][i]=max(pre[h][i-1],s[i]-s[m]);
mxn[h][i]=max(mxn[h][i-1],mxp+=a[i]);
chmax(mxp,0);
}
build(x<<1,l,m);
build(x<<1|1,m+1,r);
}
int query(int l,int r){
if(l==r)return a[l];
int h=lg[nn-1]-lg[l^r];
return max(max(mxn[h][l],mxn[h][r]),pre[h][l]+pre[h][r]);
}
}cat;
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n;
repl(i,0,n)cin>>a[i],s[i]=(i?s[i-1]:0)+a[i];
rep(i,2,n)lg[i]=lg[i>>1]+1;
nn=1<<lg[n],nn<<=nn<n;
repl(i,n+1,nn)lg[i]=lg[i>>1]+1;
cat.build();
int m;cin>>m;
while(m--){
int l,r;cin>>l>>r;
cout<<cat.query(l-1,r-1)<<"\n";
}
return 0;
}
提一嘴线性基
不难发现,线性基合并是 \(O(\log^2 w)\) 的,如果采用一般线段树维护区间线性基,那么:
- 建树复杂度为 \(O(n\log^2 w)\)
- 查询复杂度为 \(O(q\log n\log^2 w)\)
不难发现,线性基单次插入是 \(O(\log n)\) 的,如果我们使用猫树,那么
- 建树复杂度为 \(O(n\log n\log w)\)
- 查询复杂度为 \(O(q\log^2 w)\)
显然猫树复杂度严格小于普通线段树。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号