数据校验

基本概念

码距

同一编码中，任意两个合法编码之间不同二进制位数的最小值

0011与0001码距为1
0000，0011，0101，0110，1010，1100，1111码距为2（0000与1111码距为4，但从整体上看，最小值为2）

检错纠错能力

若码距 >= e + 1，可以检测e个错误
若码距 >= 2t + 1，可以纠正t个错误
若码距 >= e + t + 1 ( e > t )，则可以纠正t个错误同时检测e个错误。

奇偶校验

冗余位

只增加一个，使码距由1增加到2

编码规则

偶校验：每个码字（包括校验位）中1的数目为偶数。
奇校验：每个码字（包括校验位）中1的数目为奇数。

例：求1100的奇校验码和偶校验码（设校验位在最低位）
奇校验码：11001，偶校验码：11000

形成原理

设有效信息为D₃D₂D₁D₀
奇校验：P = ~( D3 ^ D2 ^ D1 ^ D0 )
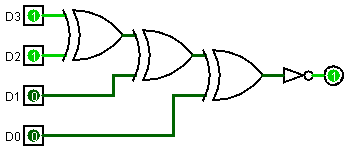
奇校验电路
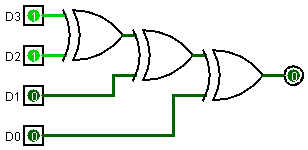
偶校验：P = D3 ^ D2 ^ D1 ^ D0
在这里插入图片描述

奇偶校验的软件实现

/*
**odd_even_parity by WWIandMC 2020/05/07
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

char*
odd_parity( char *a, int cnt, int i );

char*
even_parity( char *a, int cnt, int i );

int
main( int argc, char *argv[] )
{
	int i = 0;
	int cnt = 0;
	char buffer;
	char *a = (char*)malloc(sizeof(char));
	do{
		scanf("%c", &buffer);
		realloc( a , i + 2);
		if( buffer == '\n' ){
			break;
		}
		a[i++] = buffer;
		if( buffer == '1' ){
			cnt++;
		}
	}while(1);
	a[i] = '\0';

	printf("odd: %s\n", odd_parity(a,cnt,i));
	printf("even:%s\n", even_parity(a,cnt,i));

	return 0;
}

char*
odd_parity( char *a, int cnt, int i )
{
	if( strlen(a) != 0 ){
		if( cnt & 1 ){
			a[i++] = '0';
		}else{
			a[i++] = '1';
		}
		a[i] = '\0';
	}

	return a;
}

char*
even_parity( char *a, int cnt, int i )
{
	if( strlen(a) != 0 ){
		if( cnt & 1 ){
			a[i++] = '1';
		}else{
			a[i++] = '0';
		}
		a[i] = '\0';
	}
	
	return a;
}

校验原理

奇校验：P`` = ~( D3 ^ D2 ^ D1 ^ D0 ^ P )
奇校验：P`` = D3 ^ D2 ^ D1 ^ D0 ^ P
P``= 0，无错；若P` = 1，则有错。
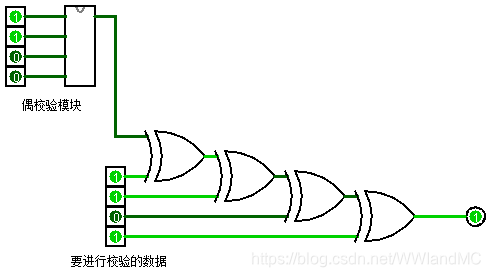
在这里插入图片描述

局限性

奇偶校验码能够发现出错情况，但不能检测偶数位错误，无错结论不可靠，也不能纠正错误。
在这里插入图片描述

海明校验

分组交叉奇偶校验码
海明校验码是怎么实现的？

海明不等式

为了能够纠正n位代码中所有可能的单错，就必须满足

k + r <= 2^r - 1

其中：
r = n - k
k为有效信息位

冗余位

按照海明不等式求出满足条件的最小r，增加r位冗余位

编码规则

信息码1011000的海明校验码

由海明不等式得到校验码位数为4
确定校验码的位置：校验码的位置由等比数列2⁰, 2¹, …, 2^r-1确定
用校验位的下标表示数据位的下标

H	1	2	1+2	4	1+4	2+4	1+2+4	8	1+8	2+8	1+2+8
bit	P₁	P₂	B₁	P₃	B₂	B₃	B₄	P₄	B₅	B₆	B₇
			1		0	1	1		0	0	0

P₁			1		1		1		1		1
P₂			2			2	2			2	2
P₃					4	4	4
P₄									8	8	8

用偶校验计算出P₁-P₄

P1 = B1 ^ B2 ^ B4 ^ B5 ^ B7 = 0
P2 = B1 ^ B3 ^ B4 ^ B6 ^ B7 = 1
P3 = B2 ^ B3 ^ B4 = 0
P4 = B5 ^ B6 ^ B7 = 0

将校验位和数据位数据填入
01100110000

形成原理

硬件

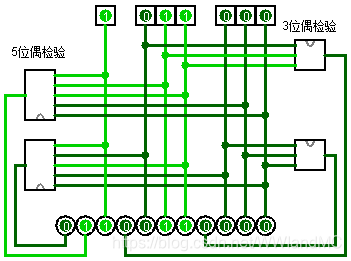
在这里插入图片描述

海明校验的软件实现

/*
**(31,5)hamming_check by WWIandMC 2020/05/07
*/
#include <stdio.h>
#include <math.h>

#define LENGTH k + r

#define DEBUG1 0

void
count_r( int k, int *r );

void
insert_check_bits( int k, int r, char *a );

void
calu_check_bits( int* tmp, int length );

int
judge_check_bit( int i );

int
main( int argc, char *argv[] )
{
	int  k; 
	int  r = 2;
	int i;
	char a[33];
	/*
	**k为有效信息位数, 最大为26位
	**r为校验位位数, 最大为5位
	*/
	scanf("%26s%n", a+1, &k);
	/*
	**方便对下标进行处理, 字符串从下标1开始存放
	*/
	count_r( k, &r );
	insert_check_bits( k, r, a );
	calu_check_bits( a, k + r );

	for( i = 1; i <= LENGTH; i++ ){
		printf("%c", a[i]);
	}

	return 0;
}

void
count_r(  int k, int *r )
{
	while( k + 1 > pow(2,*r) - *r ){
		/*计算海明不等式*/
		*r += 1;
	}
}

int
judge_check_bit( int i, int r )
{
	int LOG;
	if( i > pow(2,r-1) ){
		return 0;
	}
	LOG = ( int )( log( i ) / log( 2 ) );
	if( pow( 2, LOG ) == i ){
		return 1;
	}else{
		return 0;
	}
}

void
insert_check_bits( int k, int r, char *a )
{
	int t_boundary = k;/*临时边界, 随着校验位的插入长度会越来越大*/
	int  i, j;
	for( i = 1; i <= LENGTH; i++ ){ 
		if( judge_check_bit( i, r ) ){
			for( j = t_boundary; j >= i; j-- ){
				a[j+1] = a[j];
			}
			t_boundary++;
			a[i] = '2';/*用字符2来标记校验位*/
		}
	}
	a[LENGTH+1] = '\0';

	#if DEBUG1
	for( i = 1; i <= LENGTH; i++ ){
		printf("%c", a[i]);
	}
	printf("\n");
	#endif
}

void
calu_check_bits( char *a, int length )
{
	int i, j;
	int flag;
	char check_bit;
	unsigned int bit = 1;
	for( i = 0; pow(2,i) <= length; i++ ){
		flag = 1;
		for( j = 3; j <= length; j++ ){
			if( a[j] != '2' ){
				if( j & bit ){
					/*
					**以位来判断是否满足条件, 例如3 = 1 + 2, 二进制数为11, 3 & 1和3 & 2得到的结果都是非零
					*/
					if( flag ){
						check_bit = a[j];
						flag = 0;
					}else{
						check_bit = (check_bit - '0') ^ ( a[j] - '0' ) + '0';
					}
				}
			}
		}
		a[(int)pow(2,i)] = check_bit;
		bit <<= 1;
	}
}

校验原理

在接收端求指错字G₁-G₄

G1 = P1 ^ B1 ^ B2 ^ B4 ^ B5 ^ B7 
G2 = P2 ^ B1 ^ B3 ^ B4 ^ B6 ^ B7 
G3 = P3 ^ B2 ^ B3 ^ B4 
G4 = P4 ^ B5 ^ B6 ^ B7

若全为0则表明无错误，反之则指出错位的海明码位号

在上面的例题中，假设海明码传到接受端时，B₇发生了错误
G₁ = 1
G₂ = 0
G₃ = 1
G₄ = 1
G₄G₃G₂G₁ = 1101 = 11 指出了H11发生了错误，同时可以进行纠错
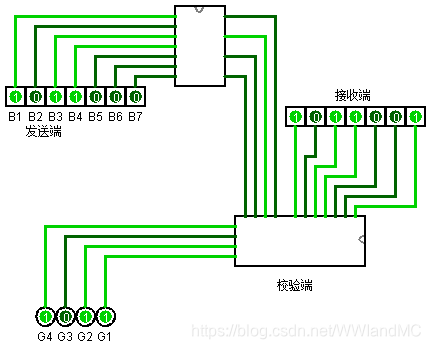
在这里插入图片描述

局限性

指错字不一定无错
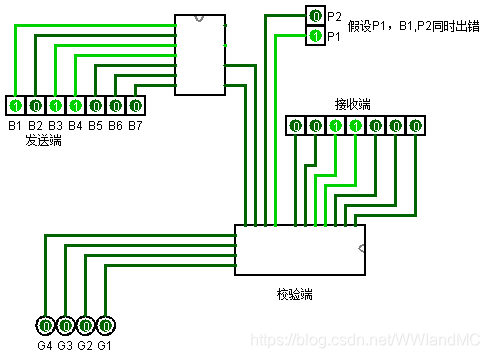
在这里插入图片描述
不能区别一位错和两位错

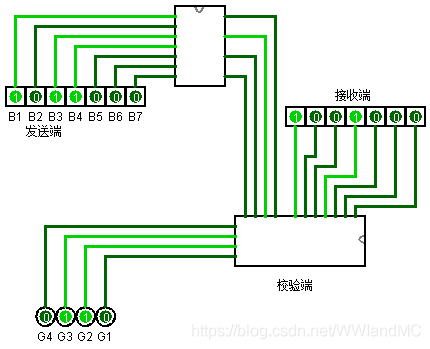
改进

已知两位同时错不改变奇偶校验的结果
可以通过增加一位奇偶校验来区分一位错还是两位错
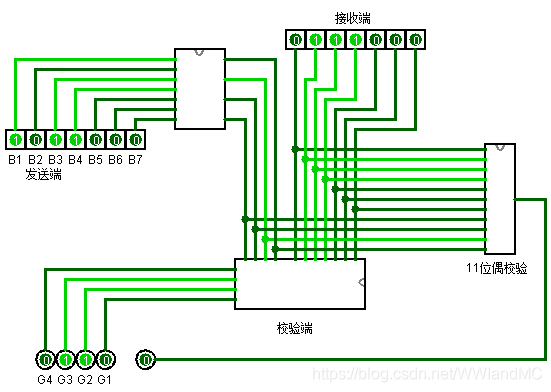
在这里插入图片描述

应用场合

存储器校验

CRC校验

Cyclic Redundancy Check

基本概念

模2运算

模2加减：加不进位，减不借位，结果和异或运算相同

模2	异或
0±0 = 0	0 ^ 0 = 0
0±1 = 1	0 ^ 1 = 1
1±0 = 1	1 ^ 0 = 1
1±1 = 0	1 ^ 1 = 0

模2除法：按模2减求部分余数
上商原则：
当部分余数首位为1时，商取1
当部分余数首位为0时，商取0
当部分余数的位数小于除数的位数时，该余数即为最后余数

生成多项式G(x)

收发双方约定的一个( r + 1 )位二进制数，发送方利用G(x)对信息多项式做模2除运算，生成校验码。接收方利用G（x）对收到的编码多项式做模2除运算检测差错及错误定位。

对于一个( n, k )CRC码来说，可将( xⁿ - 1 )分解为若干质因子，根据编码所要求的的码距选取其中的因式或若干因式的乘积作为生成多项式。

例如 x⁷ - 1 = ( x + 1 ) ( x³ + x + 1 ) ( x³ + x² + 1 )

选择G(x) = x³ + x + 1 = 1011
或者G(x) = x³ + x² + 1 = 1101

可构成( 7, 4 )码，能纠正一位错。

生成多项式应满足的条件：

任何一位发生错位都应使余数不为0
不同位发送错误应当使余数不同
对余数继续作模2除，应使余数循环

冗余位

按照海明不等式求出满足条件的最小r
给出G（x）表达式中最高项的指数

编码规则

例1：对4位信息序列1100求循环校验编码，选择生成多项式（1011）。
解法一：

待编码数据
1100( k = 4 ), M(x) = 1x³ + 1 x² + 0x¹ + 0x⁰ = x³+ x²
生成多项式代码
1011, 则G(x) = 1x³ + 0x² + 1x¹ + 1x⁰ = x³ + x¹ + 1
余数的位数r
r = G(x) 中最高项的指数，r =3。
得到：M(x) · x^r = (x³+x²)·x³ = 1x⁶ + 1x⁵ + 0x⁴ + 0x³ + 0x² + 0x¹ + 0x⁰ = x⁶ + x⁵
对应的二进制码为1100000
计算R(x)并编码
( M(x) · x³ ) 按模2除G( x )
得到余数10
M（x）·x³ 按模2加 R( x ) = 1100010

解法二：

生成多项式有4位，r = 4 - 1 = 3
将待校验的信息序列左移r位，得到1100 000
对1100 000按模2运算法则除G（x），求出CRC编码中的r位校验信息
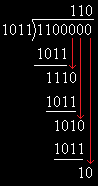
将余数10填入1100 000的最后三位，得到1100 010

CRC的软件实现

/*
**CRC_code by WWIandMC 2020/05/08
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>

#define DEBUG 0

unsigned int
string_change_to_int( int *k );

int
count_bits( unsigned int n );

unsigned int
CRC_check( unsigned int a, unsigned int g, int k_a, int k_g );

void
print_binary( unsigned int a );


int
main( int argc, char *argv[] )
{
	int  k_a, k_g;
	unsigned int a;
	unsigned int g;
	printf("Enter the information bits:");
	a = string_change_to_int( &k_a );
	printf("Enter the POLY:");
	g = string_change_to_int( &k_g );
	a = CRC_check( a, g, k_a, k_g );
	printf("The CRC code:");
	print_binary( a );
	
	return 0;
}

unsigned int
string_change_to_int( int *k )
{
	int i = 0;
	unsigned int n = 0;
	unsigned int bit = 1;
	char buffer;
	char *str = ( char* )malloc( sizeof(char) );

	do{
		scanf("%c", &buffer);
		if( buffer == '\n' ){
			break;
		}
		realloc( str, i + 2 );
		str[i++] = buffer;
	}while(1);
	str[i] = '\0';

	*k = strlen( str );

	for( i = strlen(str) - 1; i >= 0; i-- ){
		if( str[i] == '1' ){
			n |= bit;
		}
		bit <<= 1;
	}

	free(str);
	return n;
}

unsigned int
CRC_check( unsigned int a, unsigned int g, int k_a, int k_g )
{
	int flag = 1;
	int remain_bits;
	int offset;
	int cnt = k_g - 1;
	
	unsigned int remain;

	do{
		if( flag ){
			flag = 0;
			remain = a ^ ( g << ( k_a - k_g ) );
		}else{
			remain ^= g;
		}
		remain_bits = count_bits( remain );
		offset = k_g - remain_bits;
		if( cnt > 0 ){
			if( offset <= cnt ){
				remain <<= offset;
				cnt -= offset;
			}else{
				remain <<= cnt;
				cnt = 0;
			}
		}
#if DEBUG
		print_binary( remain );
#endif
	}while( cnt > 0 || count_bits(remain) == k_g );
	a <<= k_g - 1;
	a ^= remain;

	return a;
}

int
count_bits( unsigned int n )
{
	int cnt = 0;
	while( n != 0 ){
		n >>= 1;
		cnt++;
	}

	return cnt;
}

void
print_binary( unsigned int a )
{
	unsigned int bit = 1;
	bit <<= count_bits(a) - 1;
	while( bit != 0 ){
		if( a & bit ){
			printf("1");
		}else{
			printf("0");
		}
		bit >>= 1;
	}
	printf("\n");
}

校验原理

CRC余数特性分析（最多1位出错时）：
有效数字：1100，G(x) = 1011

B₇-B₁	余数
1100 010	000
1100 01_1_	001
1100 0_0_0	010
1100 _1_10	100
110_1_010	011
11_1_0 010	110
1_0_00 010	111
_0_100 010	101

对001补0做模2除，得到余数010；
对010补0做模2除，得到余数100；
对100补0做模2除，得到余数011；
对011补0做模2除，得到余数110；
对110补0做模2除，得到余数111；
对111补0做模2除，得到余数101；
对101补0做模2除，得到余数001。
再次出现了001。

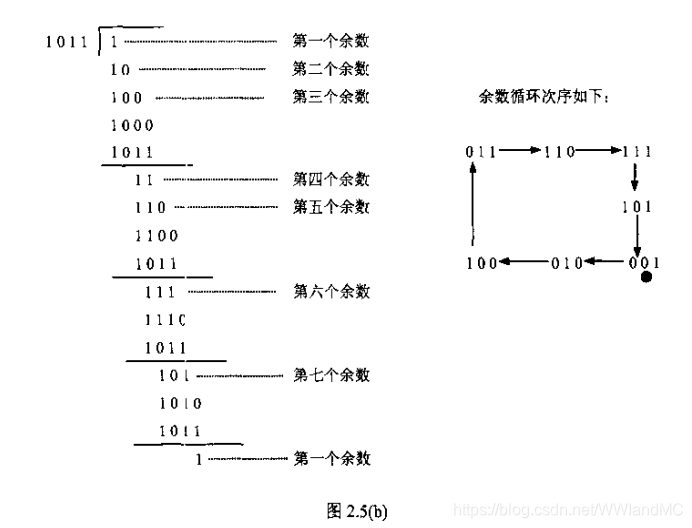
循环周期 T = 2³-1 = 7 = 数据位数

以(7, 4) CRC码, G(x) = 1011为例

根据余数循环的特点，将接收到的CRC校验码用约定的G(x)进行模2除：

余数为0，则码字无误余数不为0，则码字的某一位出错。
余数与出错位的对应关系是不变的，只和生成多项式有关。

有错时执行循环：余数补0计算新余数，CRC数据循环左移一位（把最前面的一位和最后一位互换，不丢弃数据），当新余数为001时数据最后一位取反，余数再次出现时停止。

例：数据1100110

下文的%意为模2除的余数

1100110 % 1011 = 100 （非全0，不是001）


100 0 % 1011 = 011	1100110 循环左移 1001101
011 0 % 1011 = 110	1001101 循环左移 0011011
110 0 % 1011 = 111	0011011 循环左移 0110110
111 0 % 1011 = 101	0110110 循环左移 1101100
101 0 % 1011 = 001	1101100 循环左移 1011001

将1011001最低位取反，得到1011000


001 0 % 1011 = 010	1011000 循环左移 0110001
010 0 % 1011 = 100	0110001 循环左移 1100010

余数100再次出现，循环停止
当前1100010为纠错后的数据。

校验的特点

以( 7, 4) CRC码, G(x) = 1011为例，且最多一位出错

始终将余数001作为出错位最后一位的定位依据；
每一步循环中，余数补0产生新余数，数据循环左移一位；
当余数001第1次出现时，将当前最后一位取反；
初始余数再次出现时，结束循环，刚好是2^r-1步
和海明校验不同，CRC校验无须定位出错位，仅通过1次码位取反（固定为最后一位）和2^r-1次循环操作，即可校正出错位。
如果有多位错误通常不会去纠正，纠正代价太大。

应用场合

位数较多时，循环码校验能够有效降低硬件代价，在磁介质存储和计算机之间通信等大量数据传送场景广泛应用

posted @ 2020-04-04 18:04 LanceHansen 阅读(340) 评论(0) 收藏举报

刷新页面返回顶部

LanceHansen

数据校验

基本概念

码距

检错纠错能力

奇偶校验

冗余位

编码规则

形成原理

奇偶校验的软件实现

校验原理

局限性

海明校验

海明不等式

冗余位

编码规则

形成原理

硬件

海明校验的软件实现

校验原理

局限性

改进

应用场合

CRC校验

基本概念

模2运算

生成多项式G(x)

冗余位

编码规则

CRC的软件实现

校验原理

校验的特点

应用场合

公告