树的概念
树的定义
树形式化定义
T
=
{
D
,
R
}
T=\{D,R\}
T={D,R}
D是包含n个节点的有限集合(n ≥ 0)。当n=0时为空树,否则关系R满足以下条件:
- 有且仅有一个节点d0∈D,它对于关系R来说没有前趋节点,节点d0称作树的根节点;
- 除根检点外,每个节点有且仅有一个前趋节点;
- D中每个节点可以有0个或多个后继节点。
树的递归定义
树是由n(n ≥ 0)个节点组成的有限集合(记为T)。其中:
- 如果n = 0,它是一棵空树,这是树的特例;
- 如果n > 0,有且仅有一个特定节点作为树的根节点(root),其余节点可分为m(m ≥ 0)个互不相交的有限子集T1、T2、…、Tm,而每个子集本身又是一棵树,称为根节点root的子树(SubTree)。
树的逻辑表示
树形表示法
使用一棵倒置的树表示树结构


文氏图表示法
上面的树形结构还可以用文氏图表示

凹入表示法
使用线段的伸缩关系描述树结构
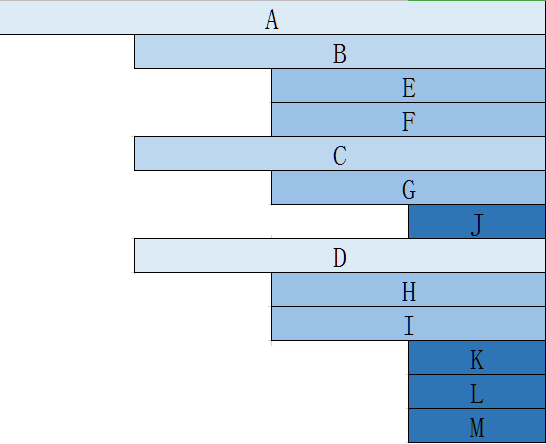
括号表示法
用一个字符串表示树
基本形式:根(子树1,子树2,…,子树m)
A
(
B
(
E
,
F
)
,
C
(
G
(
J
)
)
,
D
(
H
,
I
(
K
,
L
,
M
)
)
)
A(B(E,F),C(G(J)),D(H,I(K,L,M)))
A(B(E,F),C(G(J)),D(H,I(K,L,M)))
判断树与非树

从根节点A往下切割子树时,以C和D节点为根节点的子树不满足互不相交的定义,所以不是树。
树的基本术语
节点的度与树的度
树中一个节点的子树的个数称为该节点的度(Degree)。树中各节点的度的最大值称为树的度,通常将度为m的树称为m次树或者m叉树。

分支节点与叶子节点
度不为0的节点称为非终端节点,又叫分支节点。度为0的节点称为终端节点或叶子节点(Leaf)。
- 度为1的节点称为单分支节点;
- 度为2的节点称为双分支节点。
- 以此类推

路径与路径长度
两个节点di和dj的节点序列
(
d
i
,
d
i
1
,
d
i
2
,
.
.
.
,
d
j
)
( d_{i},d_{i1},d_{i2},...,d_{j})
(di,di1,di2,...,dj)
称为路径。其中
路径长度等于路径所通过的节点数目减1(即路径上分支数目)。

A到K的路径为A, D, I, K,其长度为3
孩子节点、双亲节点和兄弟节点
在一棵树中,每个节点的后继,被称作该节点的孩子节点(Child)。相应地,该节点被称作孩子节点的双亲节点(Parent)。具有同一双亲的孩子节点互为兄弟节点(Sibing)。

除了根节点外,每个节点有且仅有一个双亲节点
子孙节点和祖先节点
在一棵树中,一个节点的所有子树中的节点称为该节点的子孙节点(Descendant)。
从根节点到达一个节点的路径上经过的所有节点被称作该节点的祖先节点(Ancestor)。

节点的层次和树的高度
树中每个节点都处在一个层次(Level)上。节点的层次从树根开始定义,根节点为第1层,它的孩子节点为第2层,以此类推,一个节点所在的层次为其双亲节点所在的层次加1.
树中节点的最大层次称为树的高度,或树的深度(Depth)

有序树和无序树
若树中各节点的子树是按照一定的次序从左向右安排的,且相对次序是不能随意变换的,则称为有序树,否则称为无序树。

森林
n( n > 0 )棵互不相交的树的集合称为森林。
只要把树的根节点删去就成了森林。(删去根节点之后子树成林)

反之,只要给n棵独立的树加上一个节点,并把这n棵树作为该节点的子树,则森林就变成了一棵树。
独木也成林,一棵树可以看做是森林的特殊情况
树的性质
性质一
树中的节点数等于所有节点的度数+1
- 树中每个分支计为一个节点的度,所有节点的度之和等于分支数
- 根节点加上一个分支,这样分支数与节点数相等,实际分支数 = 节点数 - 1
节点数 = 度之和 + 1

例
一棵度为4的树T中,若有20个度为4的节点,10个度为3的节点,1个度为2的节点,10个度为1的节点,则树T的叶子节点个数是?
设n为总节点个数,ni为度为i(0 ≤ i ≤ m )的节点个数
n
=
n
0
+
n
1
+
n
2
+
n
3
+
n
4
=
n
0
+
10
+
1
+
10
+
20
=
n
0
+
41
\begin{aligned} n&=n_0+n_1+n_2+n_3+n_4\\ &=n_0+10+1+10+20\\ &=n_0+41 \end{aligned}
n=n0+n1+n2+n3+n4=n0+10+1+10+20=n0+41
n - 1 = 度之和
度
之
和
=
n
1
+
2
n
2
+
3
n
3
+
4
n
4
=
122
得
到
n
=
123
\begin{aligned} 度之和&=n_1+2n_2+3n_3+4n_4\\ &=122\\ 得到n&=123 \end{aligned}
度之和得到n=n1+2n2+3n3+4n4=122=123
n 0 = n − 41 = 123 − 41 = 82 n_0=n-41=123-41=82 n0=n−41=123−41=82
性质二
度为m的树中第i层上至多有mi-1个节点( i ≥ 1 )
数学归纳法证明如下
- 第一层:只有一个节点,即根节点,i = 1代入mi-1,得到1,原式成立
- 假设对于第
i-1层(i>1)命题成立,即度为m的树中第i-1层上至多有mi-2个节点,则根据树的度的定义,度为m的树中每个节点至多有m个孩子,所以第i层上的节点数至多为第i-1层上节点数的m倍,即至多为
m i − 2 × m = m i − 1 m^{i-2}\times m = m^{i-1} mi−2×m=mi−1
与命题相同,故命题成立。
性质三
高度为h的m叉树至多有
m
h
−
1
m
−
1
\frac{m^h-1} {m-1}
m−1mh−1
个节点
由性质二得,m叉树每层最多节点数
第1层:1
第2层:m1
第3层:m2
……
第h层:mh-1
1
+
m
1
+
m
2
+
.
.
.
.
.
.
+
m
h
−
1
=
m
h
−
1
m
−
1
1+m^1+m^2+......+m^{h-1}=\frac{m^h-1} {m-1}
1+m1+m2+......+mh−1=m−1mh−1
性质4
具有n个节点的m叉树的最小高度为
⌈
l
o
g
m
(
n
(
m
−
1
)
+
1
)
⌉
\lceil log_m(n(m-1)+1)\rceil
⌈logm(n(m−1)+1)⌉
⌈ ⌉为取上界的意思
设具有n个节点的m叉树的高度为h,若在该树中前h-1层都是满的,即每一层的节点数都等于mi-1个(1 ≤ i ≤ h-1),第h层(即最后一层)的节点数可能满,也可能不满,则该树具有最小的高度。

1
+
m
1
+
m
2
+
.
.
.
+
m
h
−
1
=
m
h
−
1
m
−
1
1+m^1+m^2+...+m^{h-1}=\frac{m^h-1} {m-1}
1+m1+m2+...+mh−1=m−1mh−1

1
+
m
1
+
m
2
+
.
.
.
+
m
h
−
2
+
1
1+m^1+m^2+...+m^{h-2}+1
1+m1+m2+...+mh−2+1
其高度h可计算如下
1
+
m
1
+
m
2
+
.
.
.
+
m
h
−
2
+
1
<
1
+
m
1
+
m
2
+
.
.
.
+
m
h
−
2
<
m
h
−
1
−
1
m
−
1
\begin{aligned} 1+m^1+m^2+...+m^{h-2}+1 &< 1+m^1+m^2+...+m^{h-2}\\ &< \frac{m^{h-1}-1} {m-1} \end{aligned}
1+m1+m2+...+mh−2+1<1+m1+m2+...+mh−2<m−1mh−1−1
m
h
−
1
−
1
m
−
1
<
n
≤
m
h
−
1
m
−
1
\frac{m^{h-1}-1} {m-1} \lt n \le \frac{m^h-1} {m-1}
m−1mh−1−1<n≤m−1mh−1
两边同时乘以( m-1 )
m
h
−
1
<
n
(
m
−
1
)
+
1
≤
m
h
m^{h-1} \lt n(m-1)+1 \le m^h
mh−1<n(m−1)+1≤mh
以m为底取对数
l
o
g
m
(
n
(
m
−
1
)
+
1
)
≤
h
<
l
o
g
m
(
n
(
m
−
1
)
+
1
)
log_m( n(m-1)+1) \le h \lt log_m( n(m-1)+1)
logm(n(m−1)+1)≤h<logm(n(m−1)+1)
因h只能取整数,所以
⌈
l
o
g
m
(
n
(
m
−
1
)
+
1
)
⌉
\lceil log_m(n(m-1)+1)\rceil
⌈logm(n(m−1)+1)⌉
树的最大高度为n-2



 浙公网安备 33010602011771号
浙公网安备 33010602011771号