二叉树

二叉树的定义

二叉树是有限的节点集合

  • 这个集合可以为空
  • 或由一个根节点和称为左子树和右子树的两棵互不相交的子树组成。

二叉树的子树有严格的左右之分，其次序不能任意颠倒，否则就变成了另一棵二叉树了。

分支节点的孩子节点也分为左孩子和右孩子。

二叉树的五种基本形态

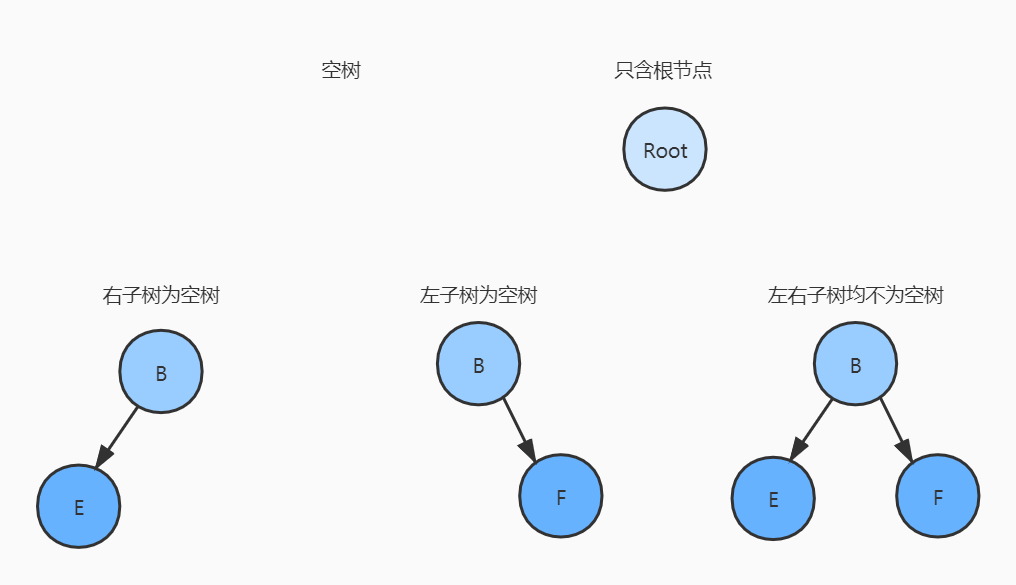
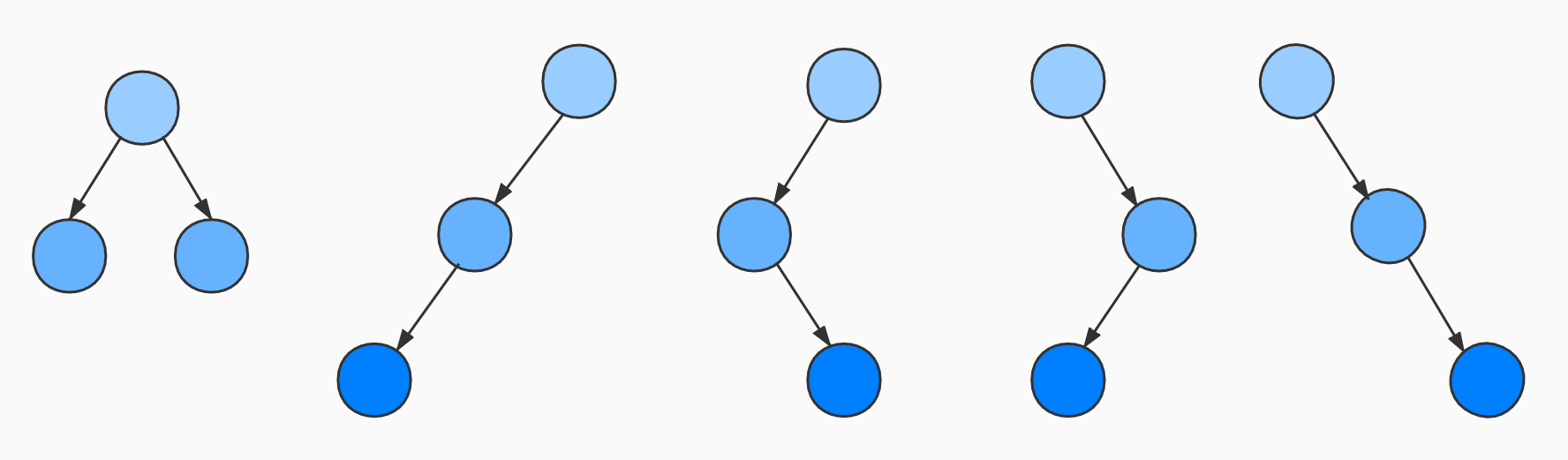
在这里插入图片描述
节点数为3的二叉树有下面5种形态，可以看出二叉树的子树是严格区分左右的。
在这里插入图片描述

特殊的二叉树

斜二叉树

Skewed Binary Tree
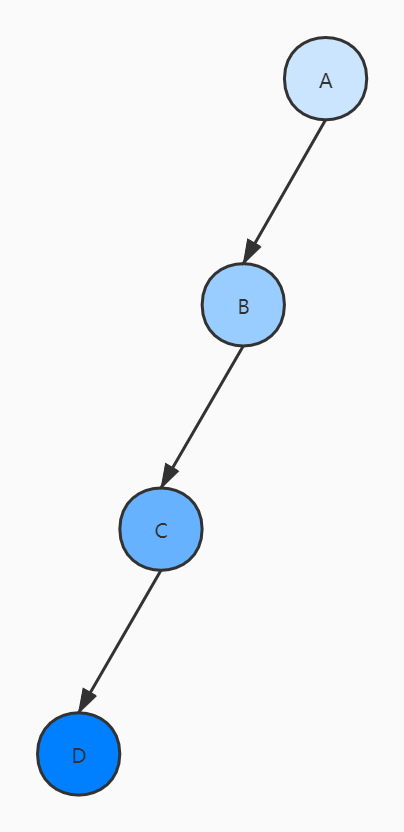
在这里插入图片描述

  • 所有的节点都只有左孩子的二叉树称为左斜树
  • 所有的节点都只有右孩子的二叉树称为右斜树

从某种意义上说，线性结构是树的一种特殊形式。

满二叉树（完美二叉树）

Full Binary Tree（Perfect Binary Tree）

在一棵二叉树中

  • 如果所有分支节点都有左子树和右子树
  • 并且叶子节点都集中在二叉树的最下一层

这样的二叉树就是满二叉树
在这里插入图片描述

高 度 为 h 的 满 二 叉 树 有 2 h − 1 个 节 点 高度为h的满二叉树有2^h-1个节点 高度为h的满二叉树有2h−1个节点

完全二叉树

Complete Binary Tree

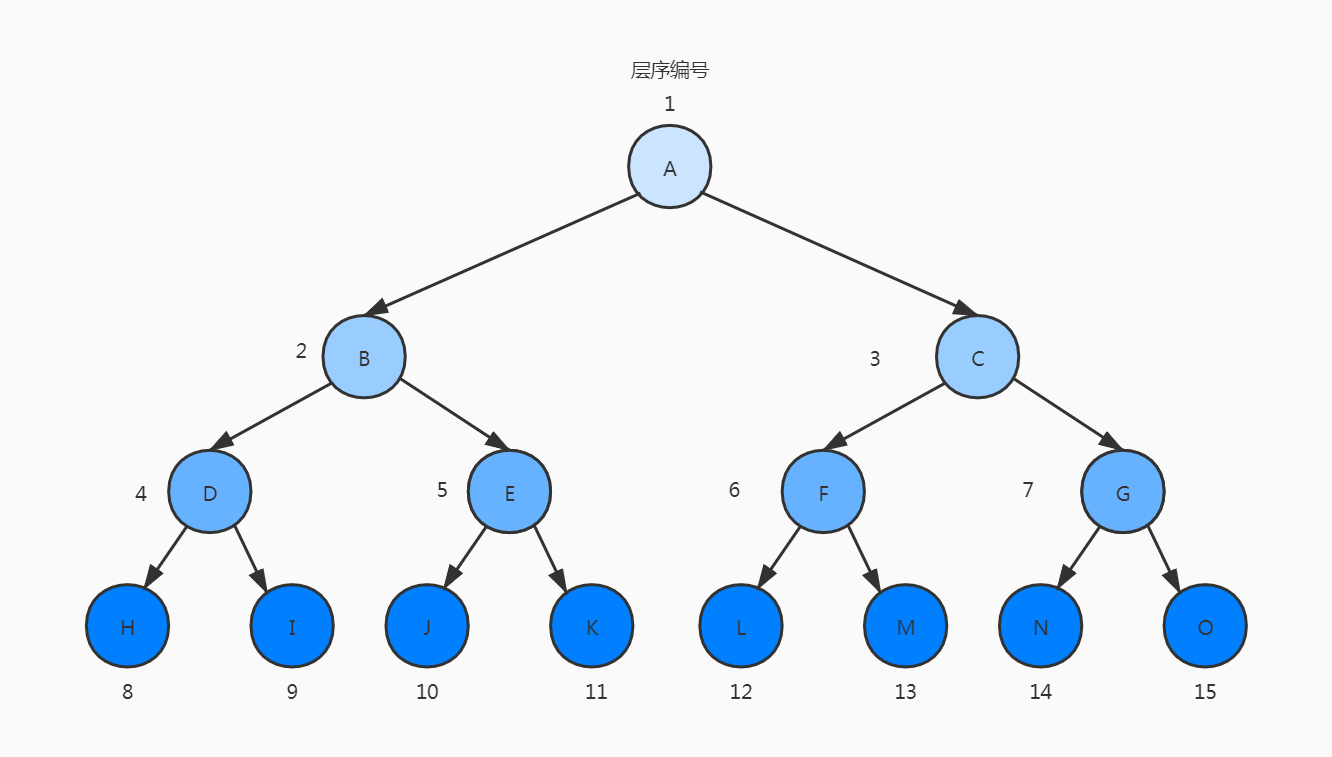
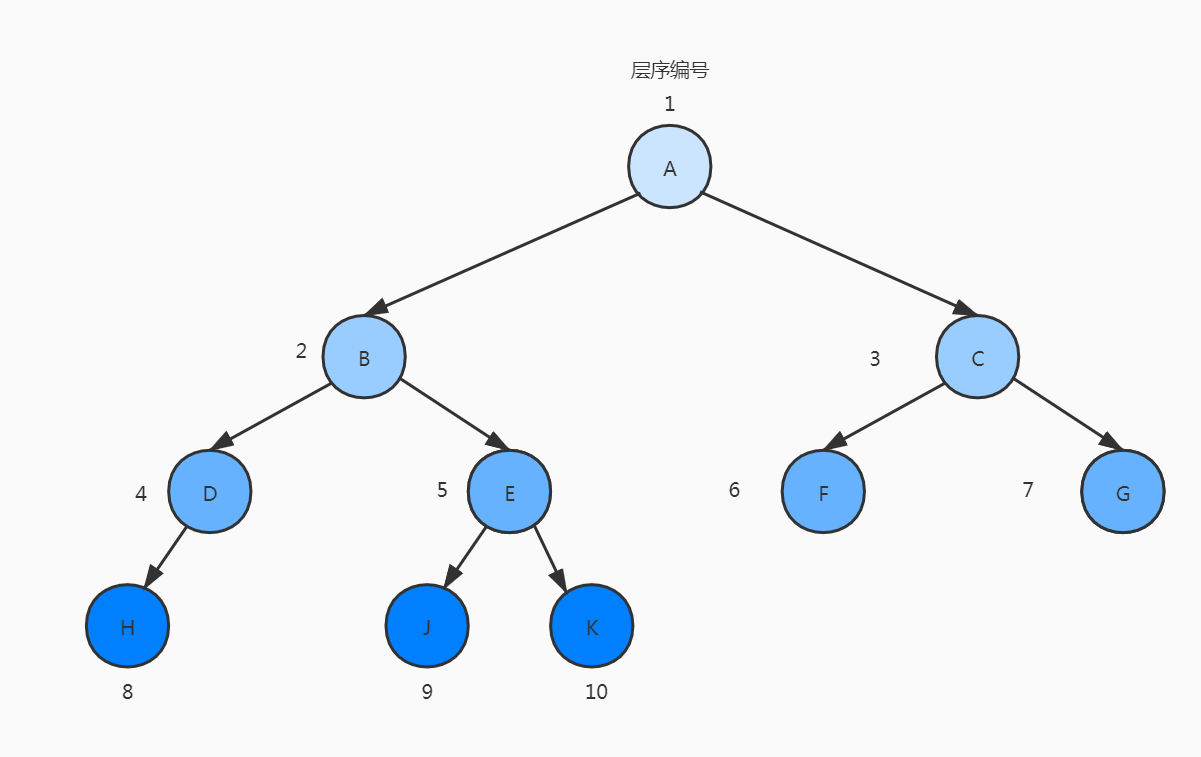
如果编号为i ( 1 ≤ i ≤ n )的节点与同样深度的满二叉树中编号为 i 的节点在二叉树中位置完全相同的，则这棵二叉树树称为完全二叉树。
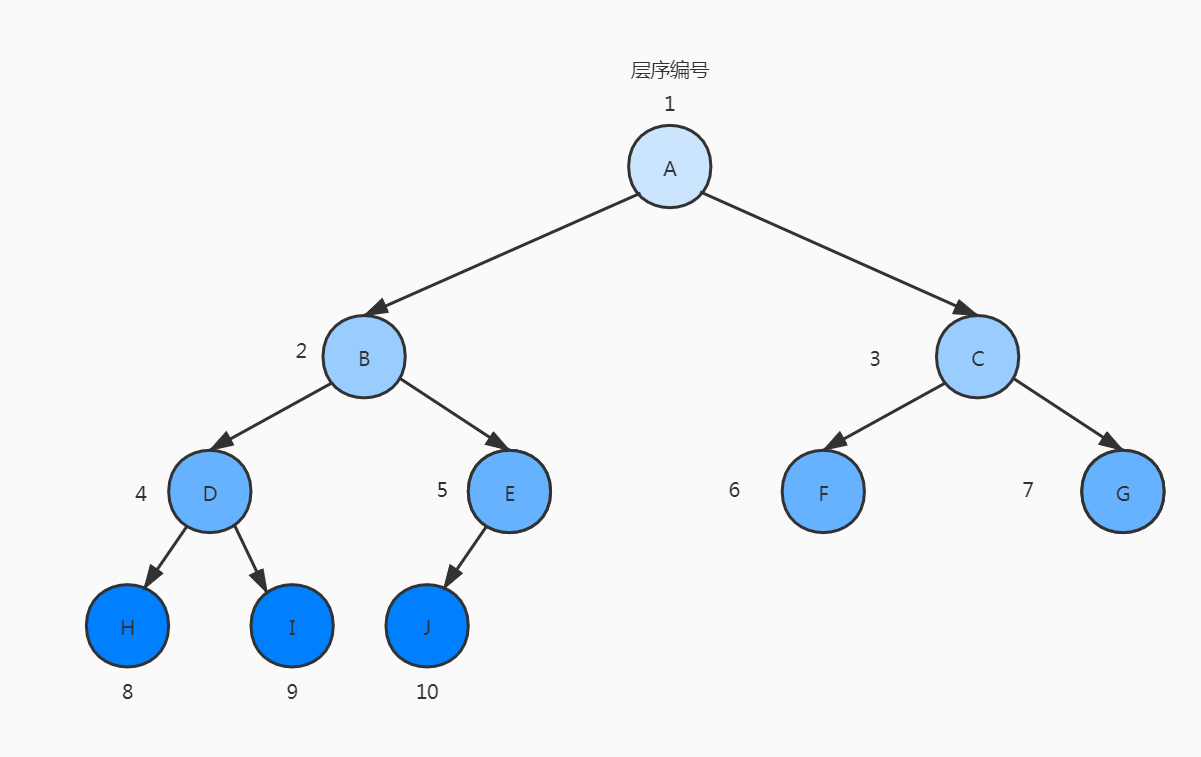
在这里插入图片描述

下面的树不是完全二叉树
在这里插入图片描述

删去了 I 节点后，J和K节点的编号变成了9和10，显然和满二叉树的位置不同，所以这棵树不是完全二叉树。

可见满二叉树实际上是一种特殊的完全二叉树。

完全二叉树的特点

  1. 叶子节点只能出现在最下两层
  2. 最下层的叶子节点一定集中在左部连续位置
  3. 如果节点的度为1，则该节点只有左孩子
  4. 同样节点数的二叉树，完全二叉树的深度最小

二叉树性质

性质一

对于任何非空二叉树T，若n0表示叶子节点的个数、n2是度为2的非叶子节点的个数，那么两者满足关系
n 0 = n 2 + 1 n_0 = n_2 + 1 n0​=n2​+1
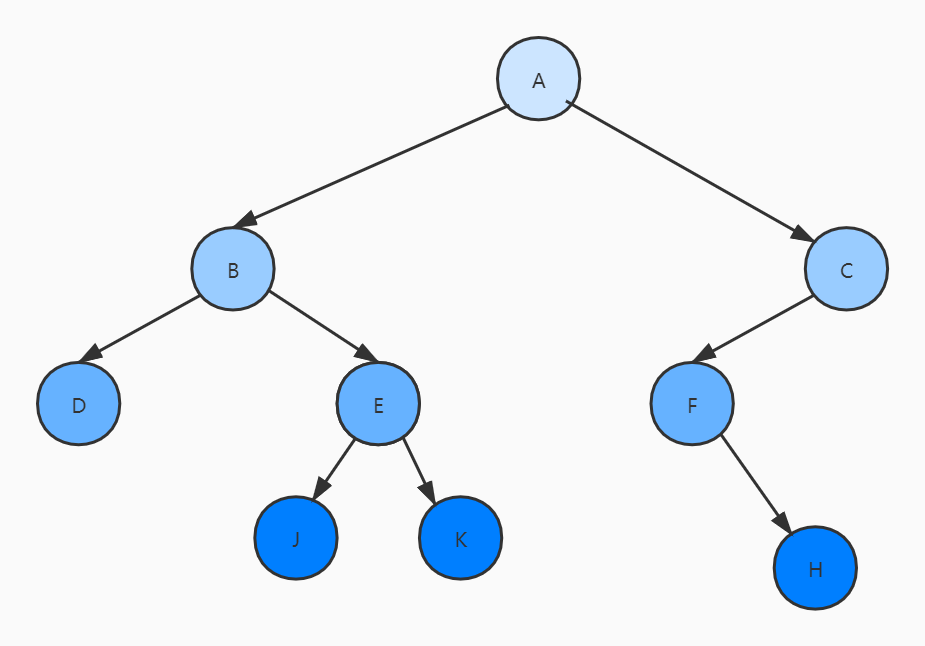
在这里插入图片描述
利用分支数的等价关系证明
首先
分 支 数 = 0 × n 0 + n 2 + 2 n 2 分支数=0 \times n_0 + n_2 + 2 n_2 分支数=0×n0​+n2​+2n2​
除了根节点之外，每个节点都有一个唯一的分支指向他于
分 支 数 = n 0 + n 1 + n 2 − 1 分支数=n_0 + n_1 + n_2 - 1 分支数=n0​+n1​+n2​−1
n 1 + 2 n 2 = n 0 + n 1 + n 2 − 1 n_1 +2n_2=n_0+n_1+n_2-1 n1​+2n2​=n0​+n1​+n2​−1
得到
n 0 = n 2 + 1 n_0 = n_2 + 1 n0​=n2​+1

例

有一棵二叉树，其两个儿子的结点个数为15个，一个儿子的结点个数为32个，问该二叉树的叶结点个数是多少？
n 0 = n 2 + 1 = 15 + 1 n_0 = n_2 + 1\\ =15+1 n0​=n2​+1=15+1

性质二

非 空 二 叉 树 上 第 i 层 上 至 多 有 2 i − 1 个 节 点 ( i ≥ 1 ) 非空二叉树上第i层上至多有2^{i-1}个节点( i \ge 1) 非空二叉树上第i层上至多有2i−1个节点(i≥1)

性质三

高 度 为 h 的 二 叉 树 至 多 有 2 h − 1 个 节 点 ( h ≥ 1 ) 高度为h的二叉树至多有2^{h-1}个节点( h \ge 1) 高度为h的二叉树至多有2h−1个节点(h≥1)

性质四

具 有 n 个 节 点 的 完 全 二 叉 树 的 深 度 为 ⌊ l o g 2 n ⌋ + 1 具有n个节点的完全二叉树的深度为 \lfloor log_2n \rfloor+1 具有n个节点的完全二叉树的深度为⌊log2​n⌋+1
对于满二叉树有
n = 2 h − 1 n=2^h-1 n=2h−1
h = l o g 2 ( n + 1 ) h=log_2(n+1) h=log2​(n+1)
在高度h不变的情况下，讨论节点数的取值范围

  • 最多的情况是满二叉树
  • 最少的极限是高度为h-1的满二叉树
    2 k − 1 − 1 < n ≤ 2 h − 1 2^{k-1}-1 \lt n \le 2^h-1 2k−1−1<n≤2h−1

放缩不等式
n ≤ 2 h − 1 → n < 2 h n\le2^h-1 → n < 2^h n≤2h−1→n<2h
2 h − 1 − 1 < n → 2 h − 1 ≤ n 2^{h-1}-1 < n→2^{h-1}\le n 2h−1−1<n→2h−1≤n
所以

2 h − 1 ≤ n < 2 h 2^{h-1}\le n \lt 2^h 2h−1≤n<2h
取对数
h − 1 ≤ l o g 2 n < h h-1 \le log_2n < h h−1≤log2​n<h
得到
h = ⌊ l o g 2 n ⌋ + 1 h = \lfloor log_2n \rfloor+1 h=⌊log2​n⌋+1

性质五

对完全二叉树中编号为i的节点
1. 若 i = 1 ， 则 节 点 是 二 叉 树 的 根 ; 若 i > 1 ， 则 其 双 亲 节 点 为 ⌊ i 2 ⌋ 1.若i=1，则节点是二叉树的根;若i>1，则其双亲节点为\lfloor \frac i 2 \rfloor 1.若i=1，则节点是二叉树的根;若i>1，则其双亲节点为⌊2i​⌋
2. 若 2 i > n , 则 节 点 i 是 叶 子 节 点 没 有 左 孩 子 ， 否 则 其 左 孩 子 为 2 i 2.若2i>n,则节点i是叶子节点没有左孩子，否则其左孩子为2i 2.若2i>n,则节点i是叶子节点没有左孩子，否则其左孩子为2i
3. 若 2 i + 1 > n , 则 节 点 i 无 右 孩 子 , 否 则 其 右 孩 子 为 2 i + 1 3.若2i+1>n,则节点i无右孩子,否则其右孩子为2i+1 3.若2i+1>n,则节点i无右孩子,否则其右孩子为2i+1

二叉树和树、森林之间的变换

树变换为二叉树

采用孩子兄弟表示法的思想，增加指向右兄弟的指针，保留第一个孩子节点指针，移除其他孩子指针。
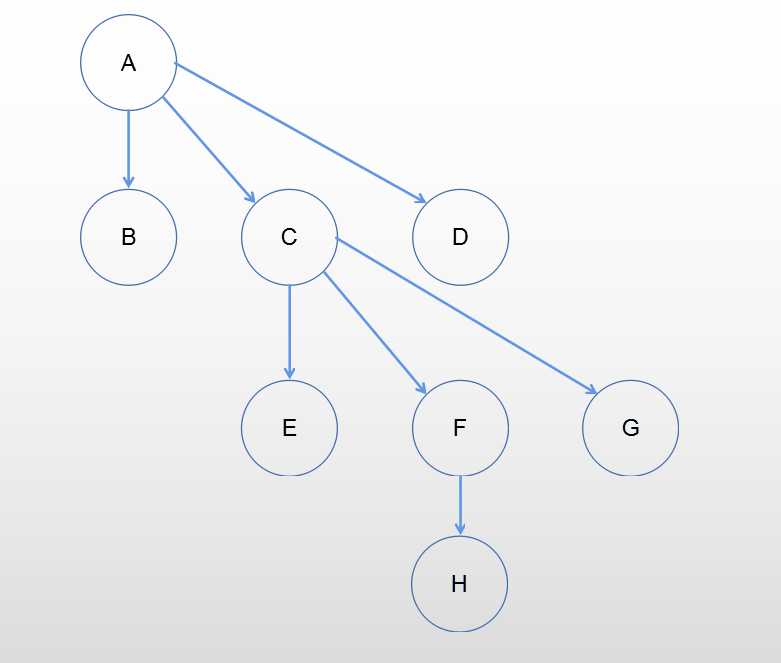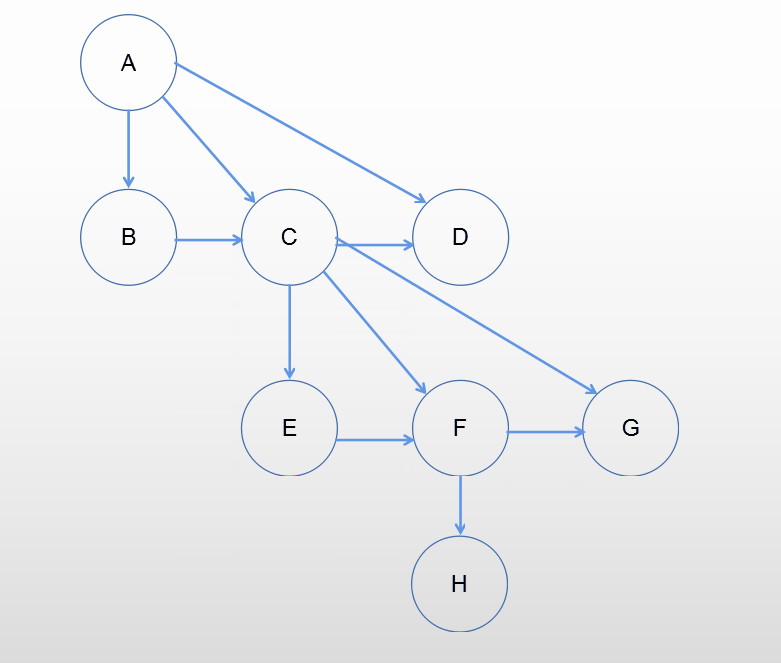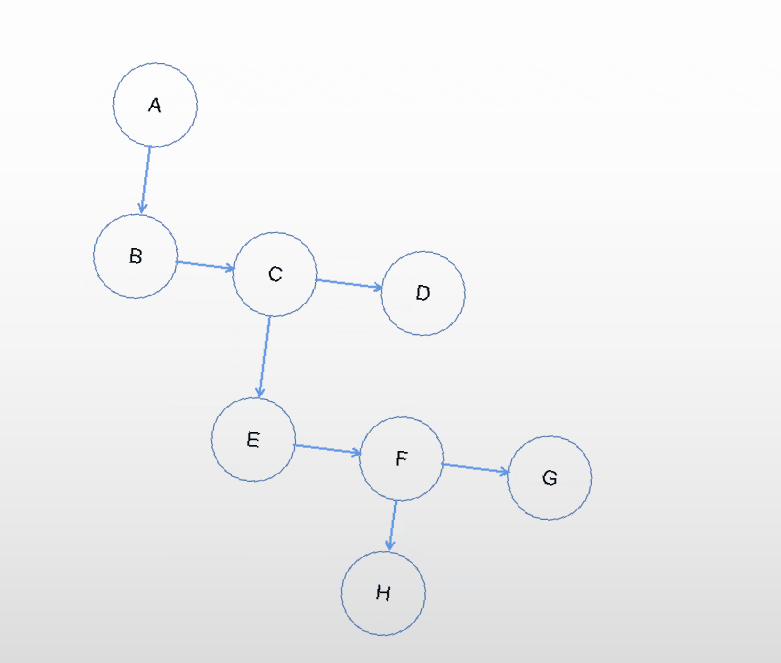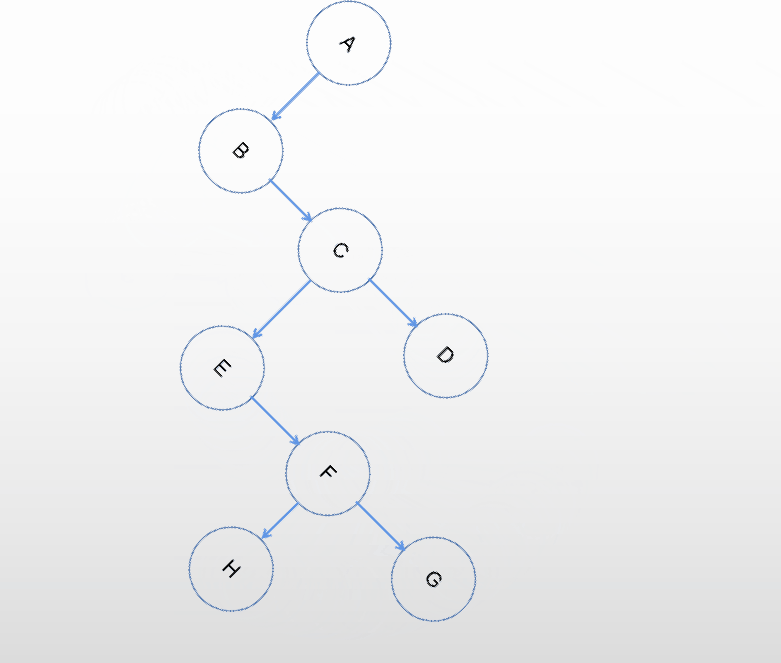
在这里插入图片描述

森林转换为二叉树

增加一个辅助根节点，和上面的思路相同。
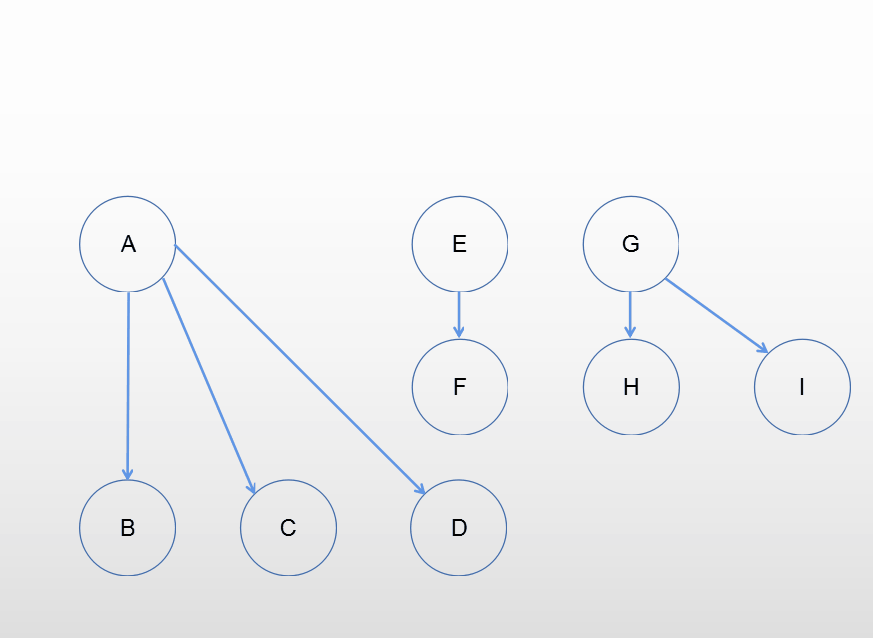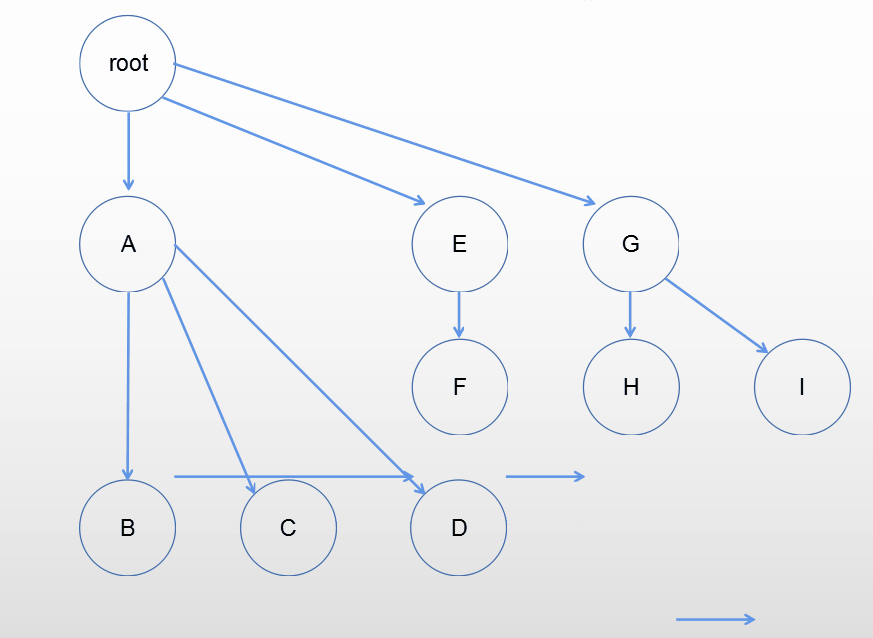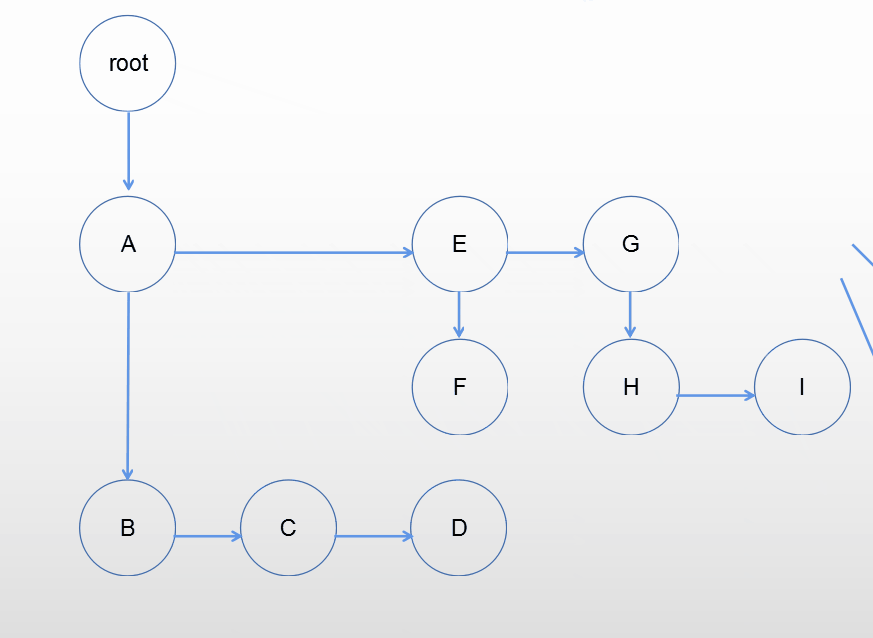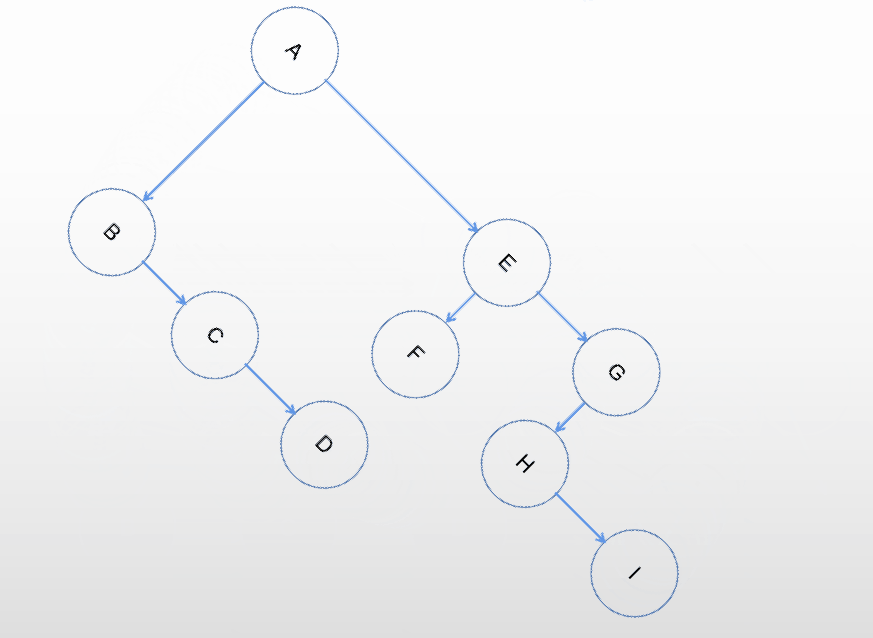
在这里插入图片描述

二叉树还原成树、森林

和上面的步骤相反即可

二叉树还原成树

二叉树还原成森林

posted @ 2020-08-03 01:15  LanceHansen  阅读(318)  评论(0)    收藏  举报