图的概念
图的定义
图（Graph）G由顶点（Vertex）集合V(G)和边（Edge）集合E(G)构成。
G
=
(
V
,
E
)
G = (V,E)
G=(V,E)
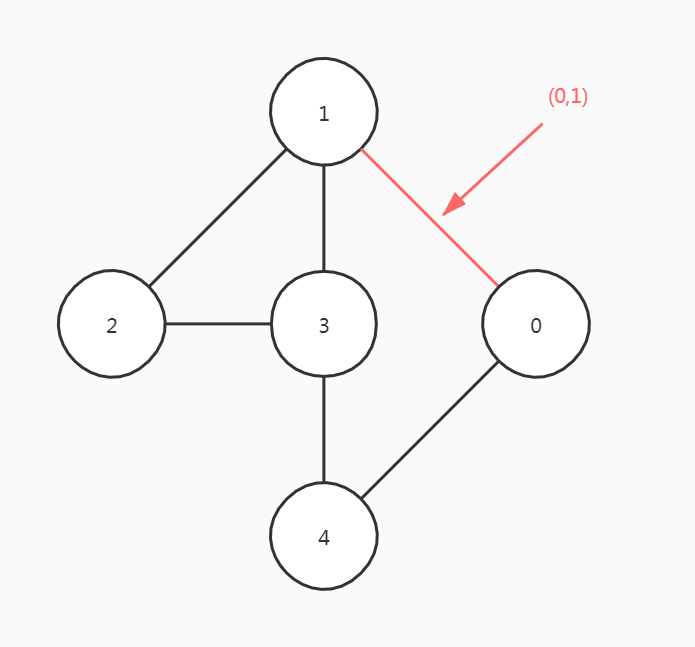
在图G中，如果代表边的顶点对是无序的，则称G为无向图。用圆括号序偶表示无向边
(0,1)也可以写成(1,0)
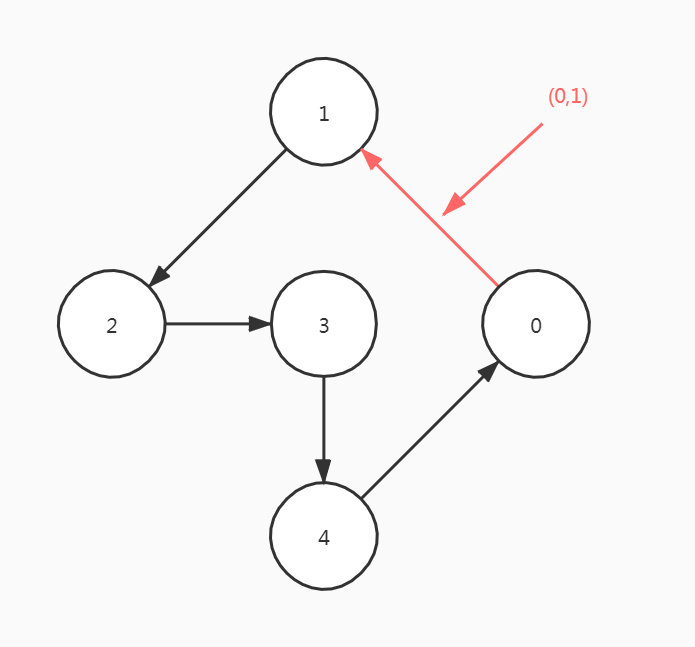
如果表示边的顶点对是有序的，则称G为有向图。用尖括号序偶表示有向边（又称弧 Arc）
不能写成<1,0>
图的基本术语
端点和邻接点
无向图
若存在一条边(i, j)，则称顶点i和顶点j为这条边的两个端点，它们互为邻接点（Adjacent），边( i, j )依附（incident）于顶点i和顶点j。
有向图
若存在一条边<i, j>，则称顶点i为起始端点，简称起点，顶点j为终止端点，简称终点，它们互为邻接点
顶点的度、入度和出度
无向图
以顶点i为端点的边数称为该顶点的度(Degree)
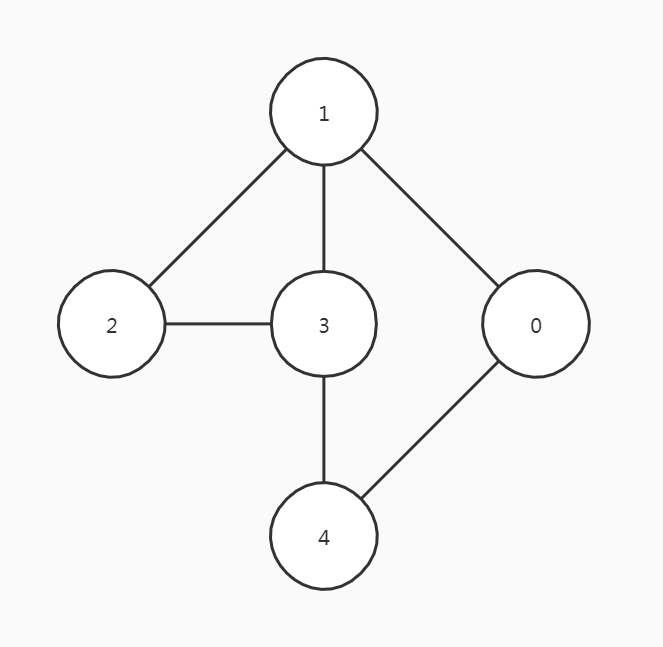如图，顶点1的度为3
有向图
以顶点i为终点的入边的数目，称为该顶点的入度（InDegree）。
以顶点i为起点的出边的数目，称为该顶点的出度（OutDegree）。
一个顶点的入度和出度的和为该顶点的度。
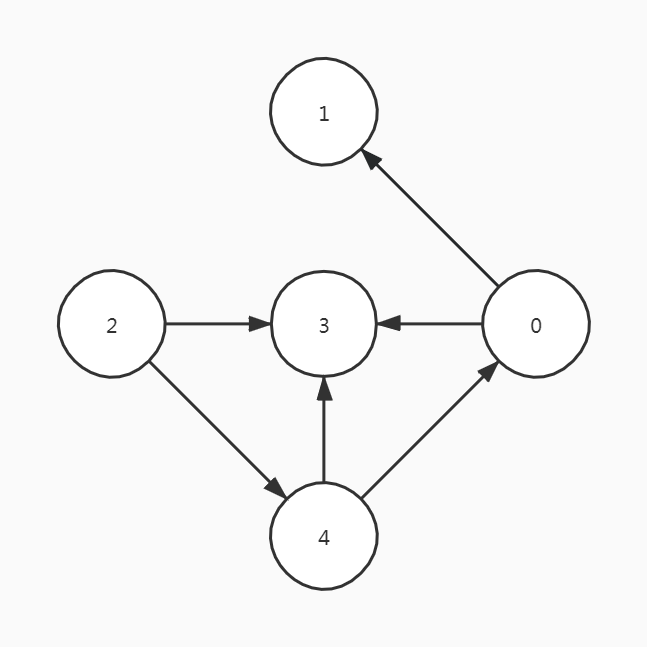
如图
- 顶点0的入度为1
- 顶点0的出度为2
- 顶点0的度为1+2=3
若一个图中有n个顶点和e条边，每个顶点的度为di(0 ≤ i ≤ n-1)
e
=
1
2
∑
i
=
0
n
−
1
d
i
e= \frac 1 2\displaystyle\sum^{n-1}_{i=0}d_i
e=21i=0∑n−1di
完全图
无向图
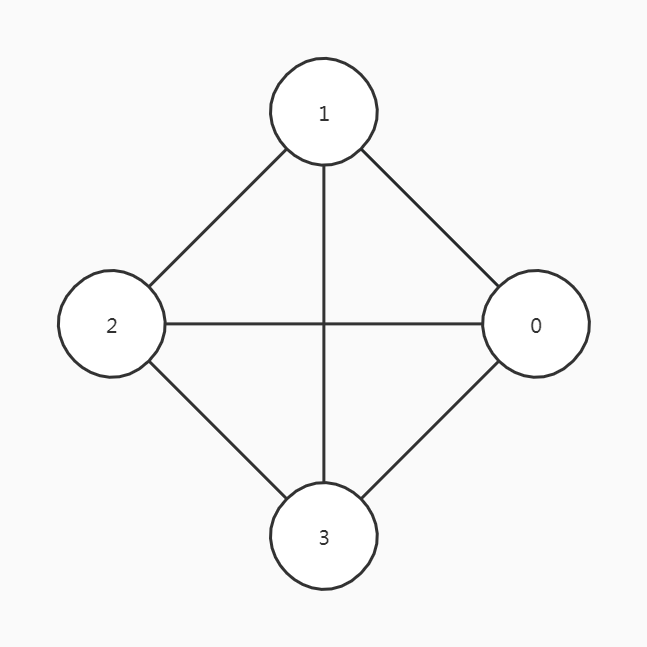
每两个顶点之间都存在一条边，称为完全无向图，包含有
n
(
n
−
1
)
2
条
边
\frac {n(n-1)} 2 条边
2n(n−1)条边
有向图
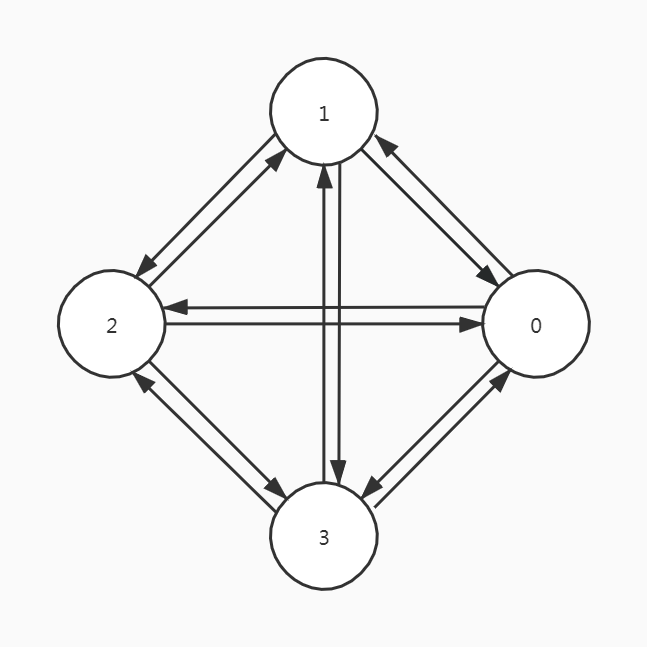
每两个顶点之间都存在着方向相反的两条边，称为完全有向图，包含有
n ( n − 1 ) 条 边 n(n-1)条边 n(n−1)条边
稠密图和稀疏图
当一个图接近完全图时，则称为稠密图
相反，当一个图含有较少的边数
e
<
<
n
(
n
−
1
)
e \lt \lt n(n-1)
e<<n(n−1)
时，则称为稀疏图
子图
设有两个图
G
=
(
V
,
E
)
G
′
=
(
V
′
,
E
′
)
G=(V,E)\\ G\rq=(V\rq,E\rq)
G=(V,E)G′=(V′,E′)
若
V
′
⊆
V
且
E
′
⊆
E
V\rq \sube V 且 E\rq \sube E
V′⊆V且E′⊆E
则称G`是G的子图。
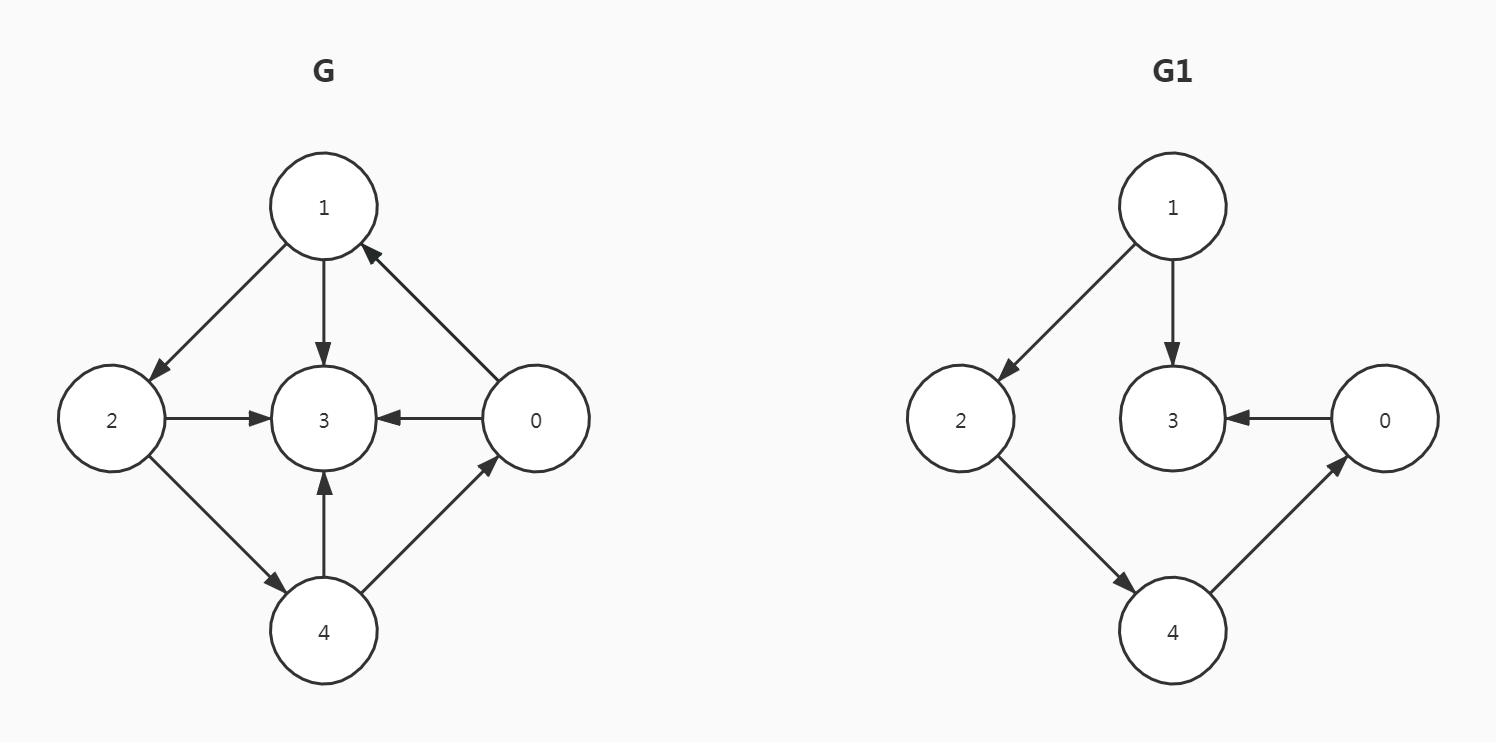
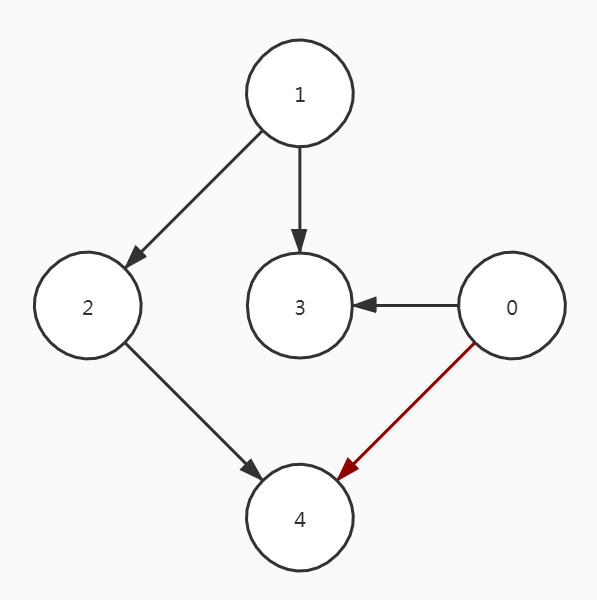
下面这个图不是G的子图
路径和路径长度
在一个图
G
=
(
V
,
E
)
G = ( V, E )
G=(V,E)
从顶点i到顶点j的一条路径（Path）是一个顶点序列
(
v
i
,
v
i
1
,
v
i
2
,
.
.
.
,
v
i
m
,
v
j
)
( v_i, v_{i1},v_{i2},...,v_{im},v_j)
(vi,vi1,vi2,...,vim,vj)
其中所有的
(
i
x
,
i
y
)
∈
E
(
G
)
或
<
i
x
,
i
y
>
∈
E
(
G
)
( i_x, i_y ) \in E(G) 或 < i_x, i_y > \in E(G)
(ix,iy)∈E(G)或<ix,iy>∈E(G)
路径长度是指一条路径上经过的边的数目。
若一条路径上除开始点和结束点可以相同外，其余顶点均不相同，则称此路径为简单路径。
如图， 由v0到v1的一条简单路径，长度为2
回路（环）
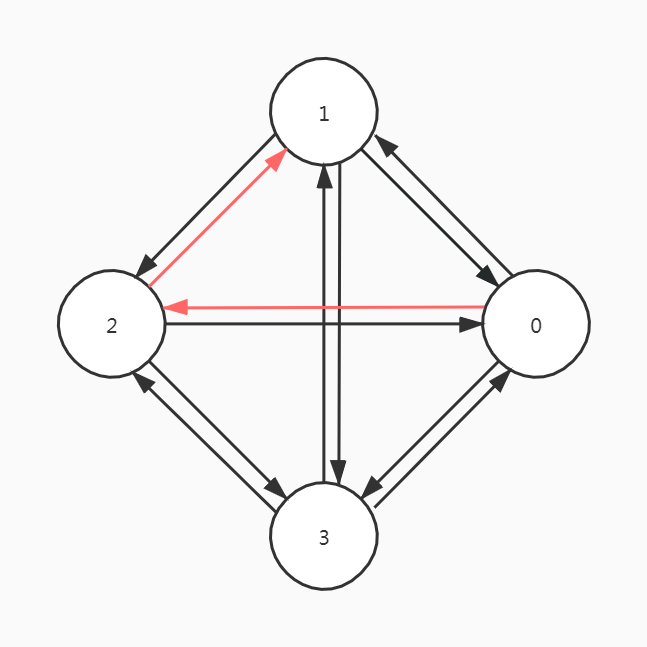
若一条路径上的开始点与结束点为同一个顶点，则此路径被称为回路或环（Cycle）。开始点与结束点相同的简单路径被称为简单回路或简单环。
如图，红色路径即为一条简单回路。
连通、连通图和连通分量
无向图
在无向图中，若从顶点i到顶点j有路径，则称顶点i和j是连通的。
若图中任意两个顶点都连通，则称为连通图（Connected Graph），否则称为非连通图。
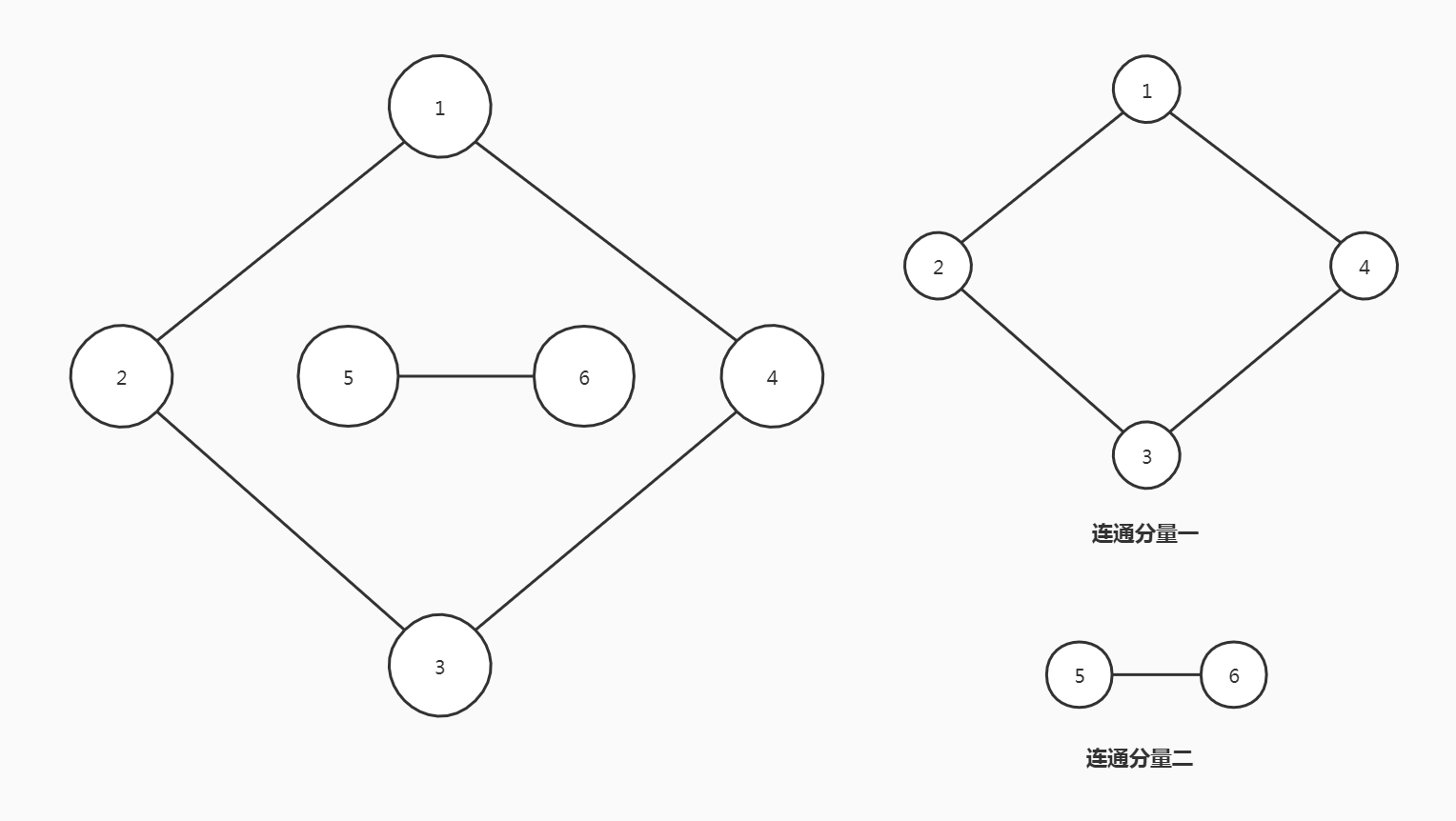
无向图G中的极大连通子图称为G的连通分量。显然，任何连通图的连通分量只有一个，即本身，而非连通图有多个连通分量。
一个连通分量
- 要是子图
- 这个子图要是连通的
- 这个连通子图含有极大顶点数
- 具有极大顶点数的连通子图包含依附于这些顶点的所有边
有向图
若从顶点i到顶点j有路径，则称从顶点i和顶点j是连通的
若图G中的任意两个顶点i和j都连通，即从顶点i到j和从顶点j到i都存在路径，则称图G是强连通图
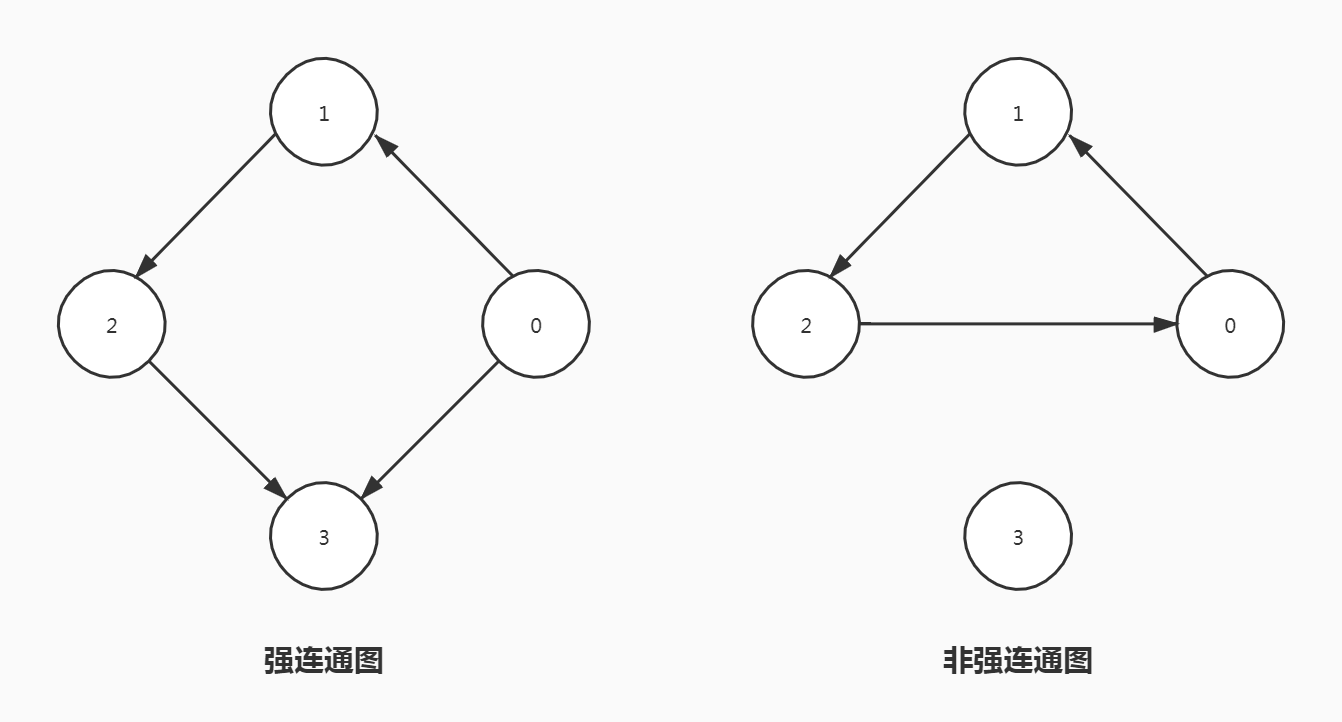
有向图G中的极大强连通子图称为G的强连通分量。显然，强连通图只有一个强连通分量，即本身。非强连通图有多个强连通分量。
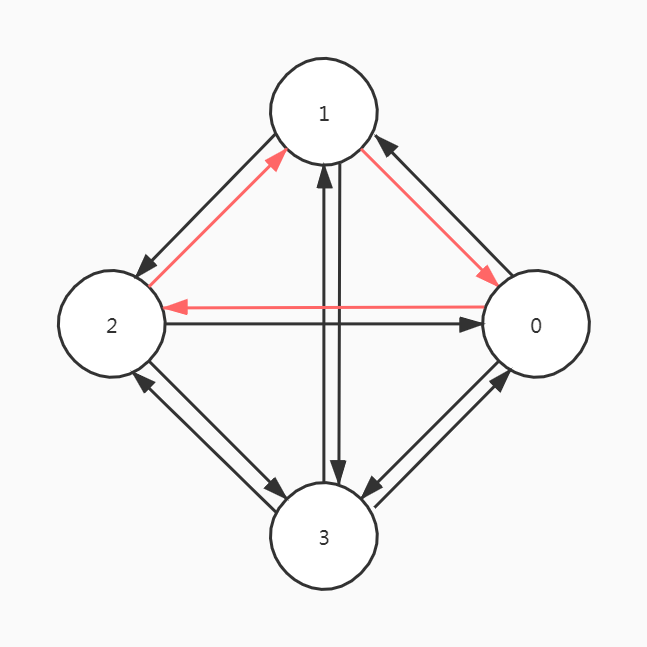
在一个非强连通图中找强连通分量的方法
- 在图中找有向环
- 扩展该有向环
如果某个顶点到该环中任一顶点有路径，并且该环中任一顶点到这个顶点也有路径，则加入这个顶点。
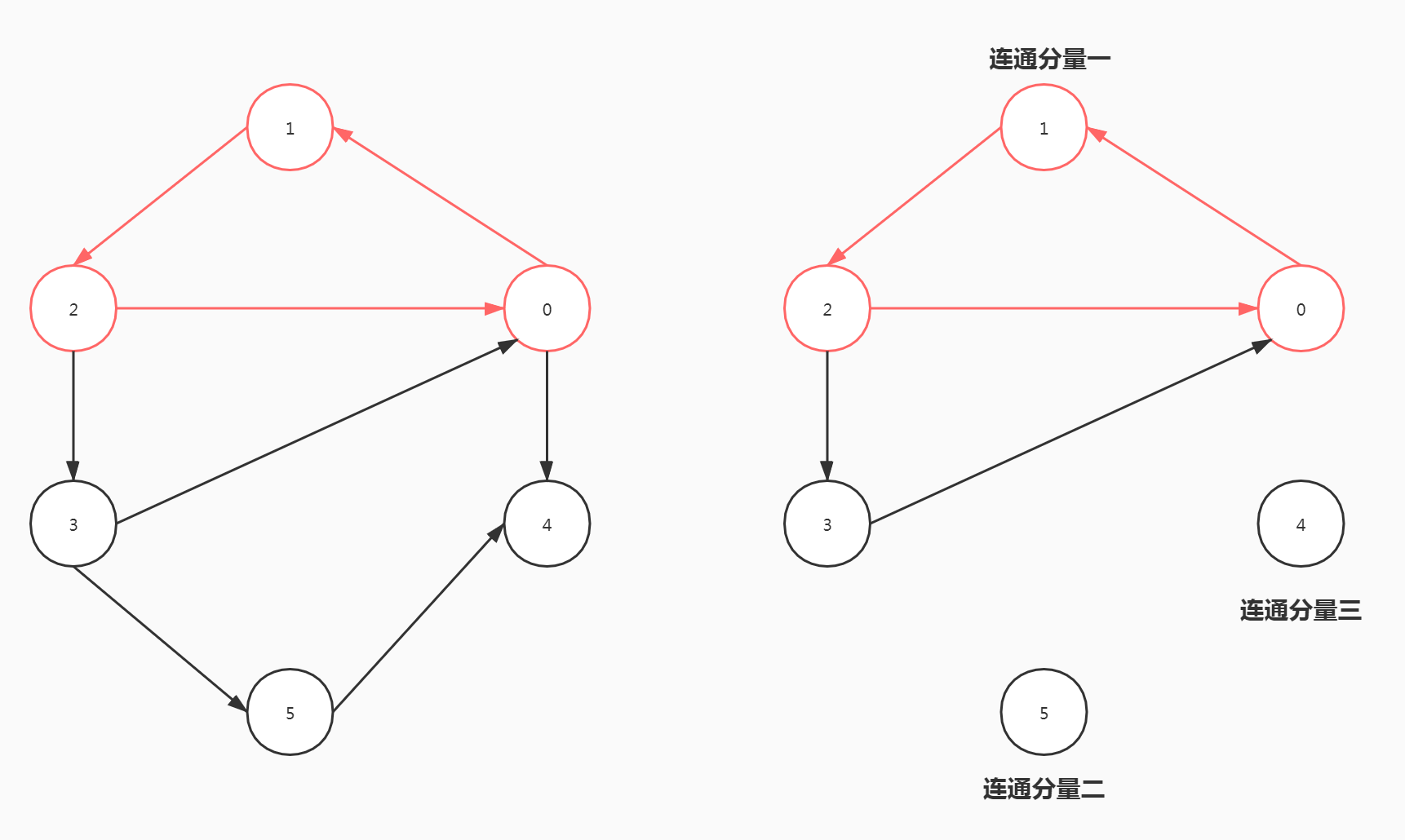
红色标记即为一个有向环，图中3号顶点满足条件，加入该环，而5号顶点不满足条件，因为3可以到5，但5不能到3。同理，0可以到4但4不可以到0。所以该图有三个强连通分量。
权和网
图中每一条边都可以附带有一个对应的数值，这种与边相关的数值称为权（Weight）。权可以表示从一个顶点到另一个顶点的距离或花费的代价。
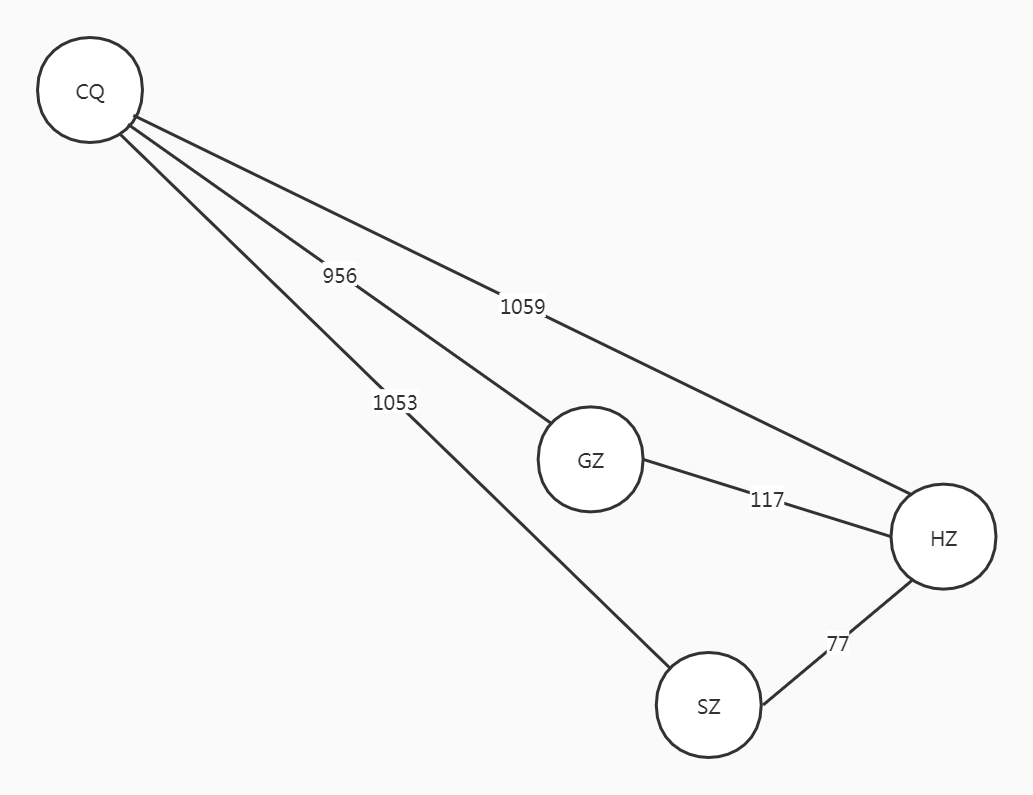
边上带有权的图称为带权图，也称作网（Network）
浙公网安备 33010602011771号