图的遍历 DFS BFS

从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历（Traversing Graph）

深度优先遍历

Depth First Search
又称深度优先搜索，简称为DFS

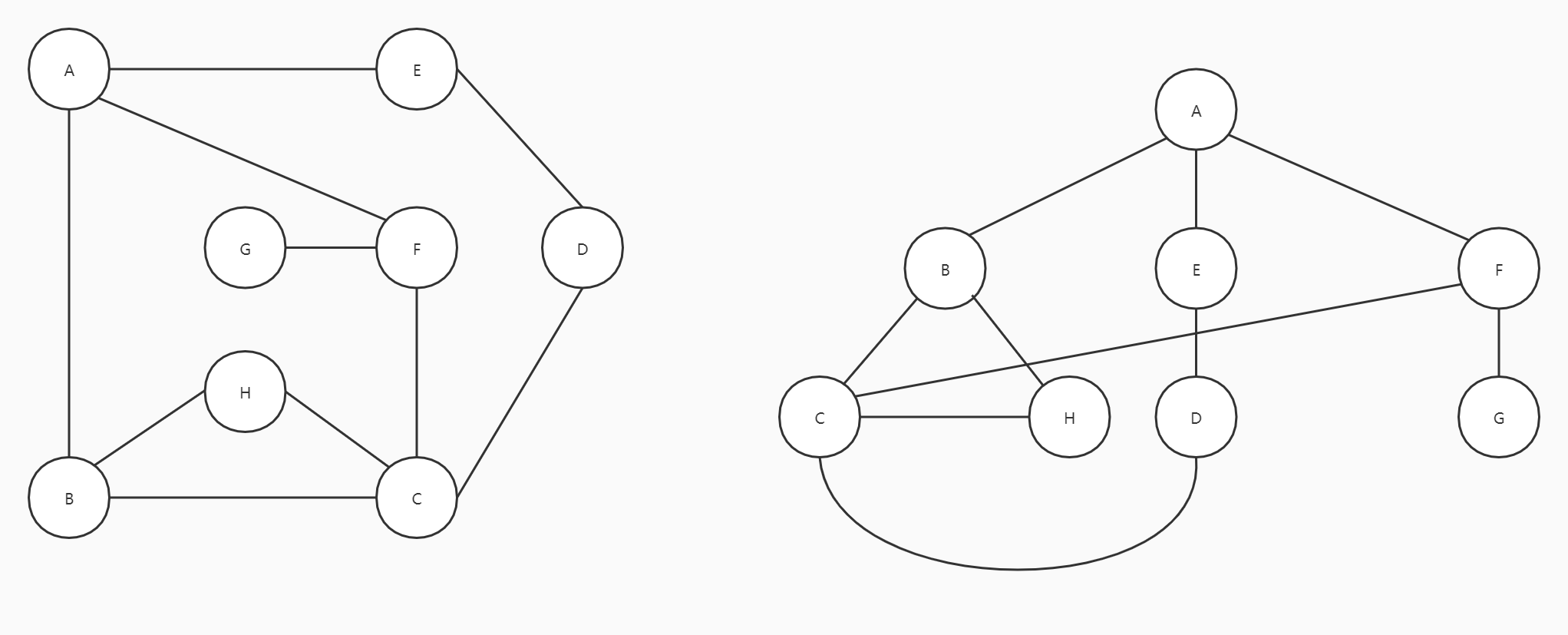
以这张图为例，从顶点A开始

约定一个规则：有多个选择的情况下，始终往右手边走

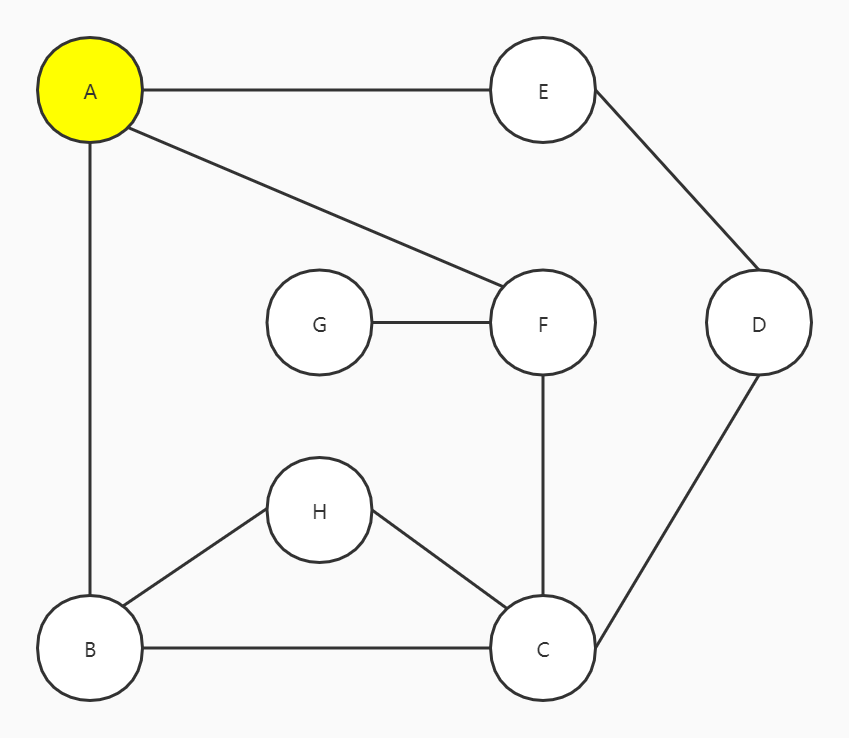
A有三个邻接点，E、F和B，往右走到B

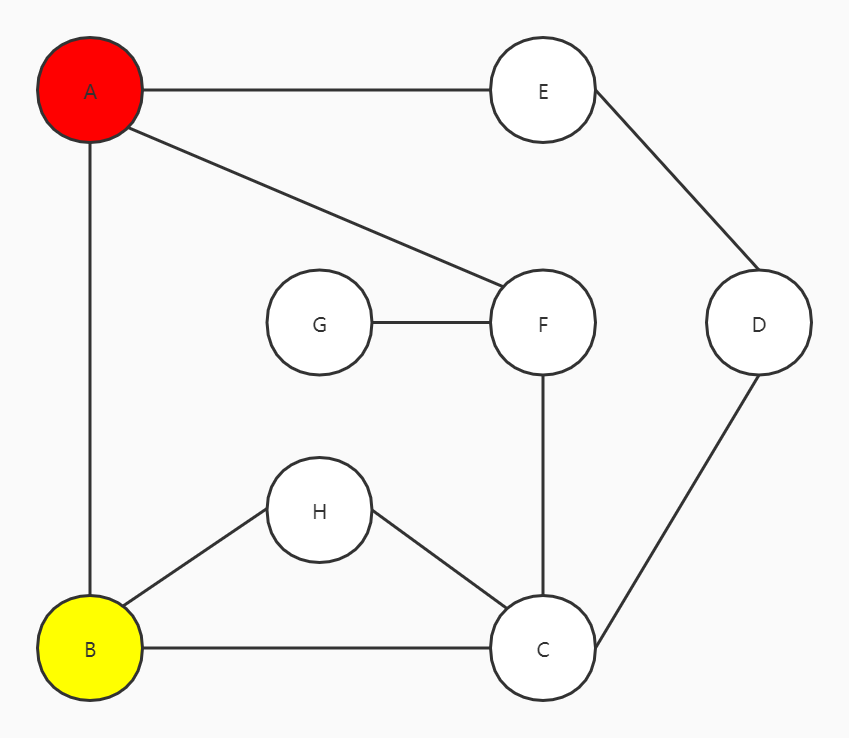
B有三个邻接点，A、H和C，A已经走过来，所以在H和C当中选择，往右走到C

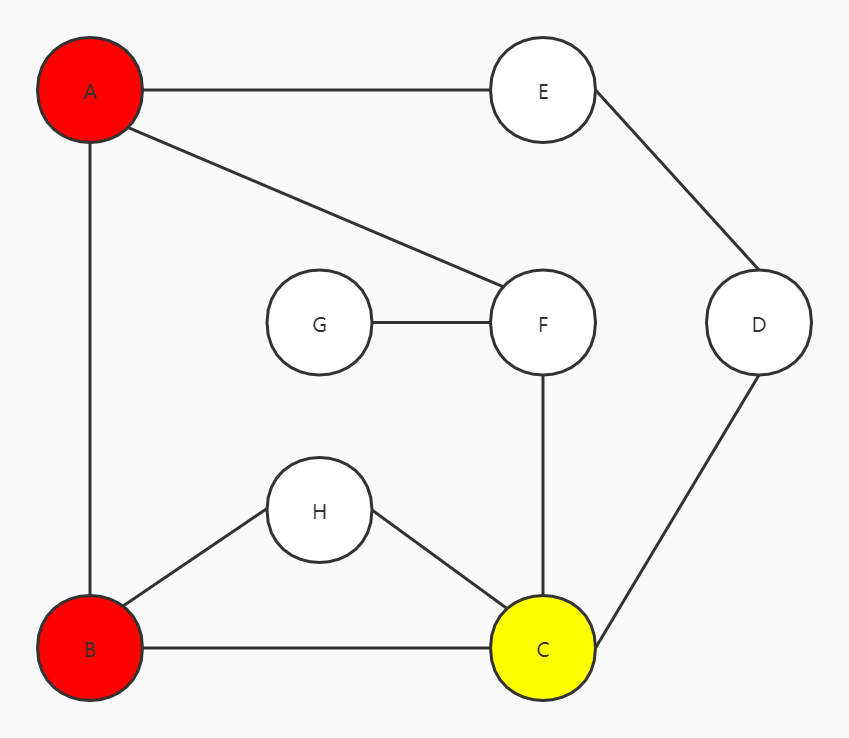
C有四个邻接点，B、H、F和D，往右走到D

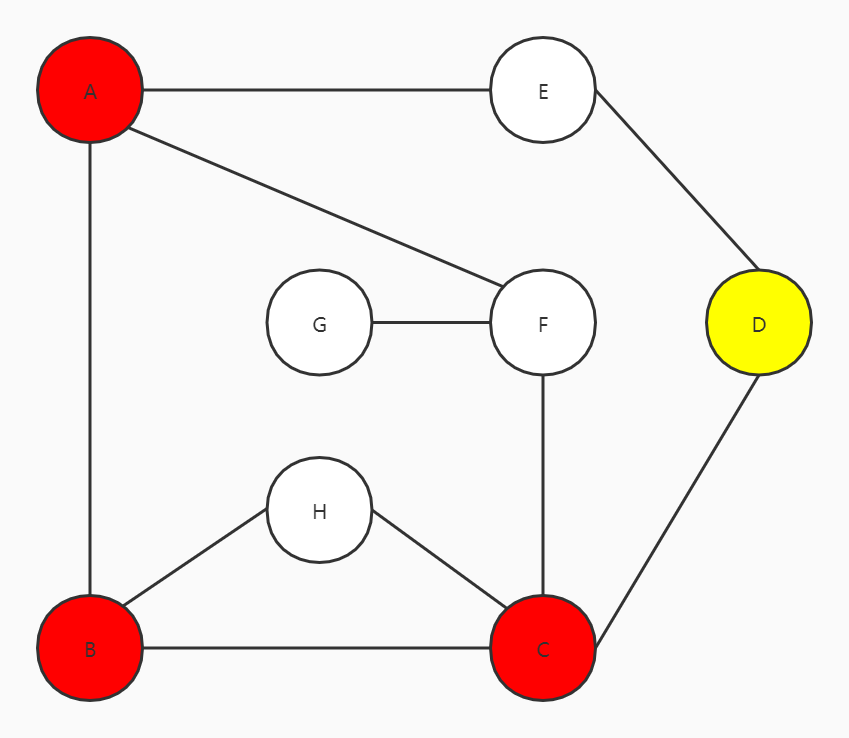
D走到E

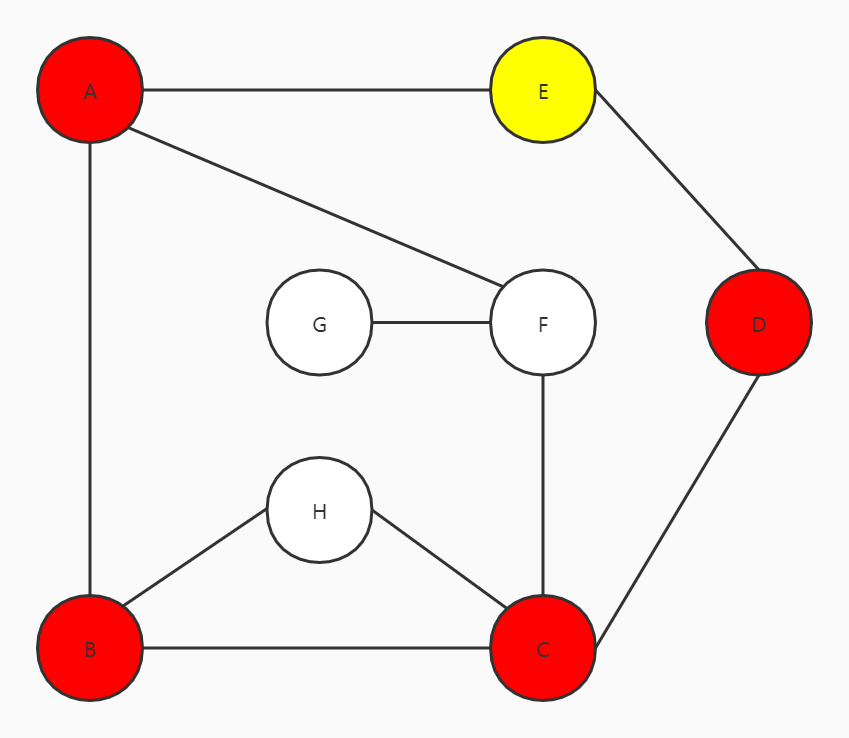
此时，E的两个邻接点都已经走过了，但图中仍有顶点没有访问过，此时按原路返回（和栈有关）

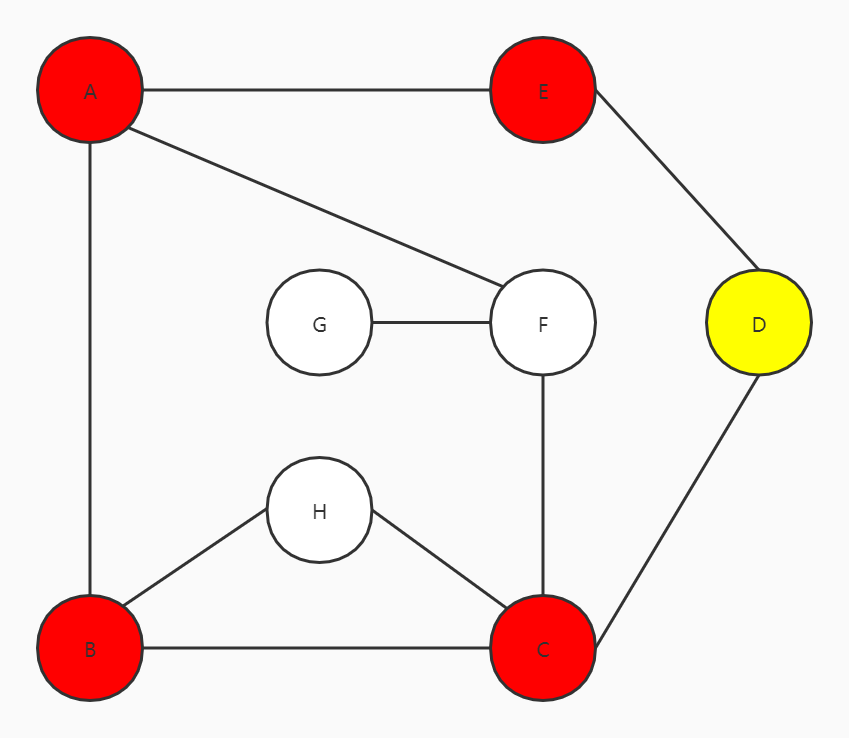
D的两个邻接点E和C也已经走过，继续原路返回

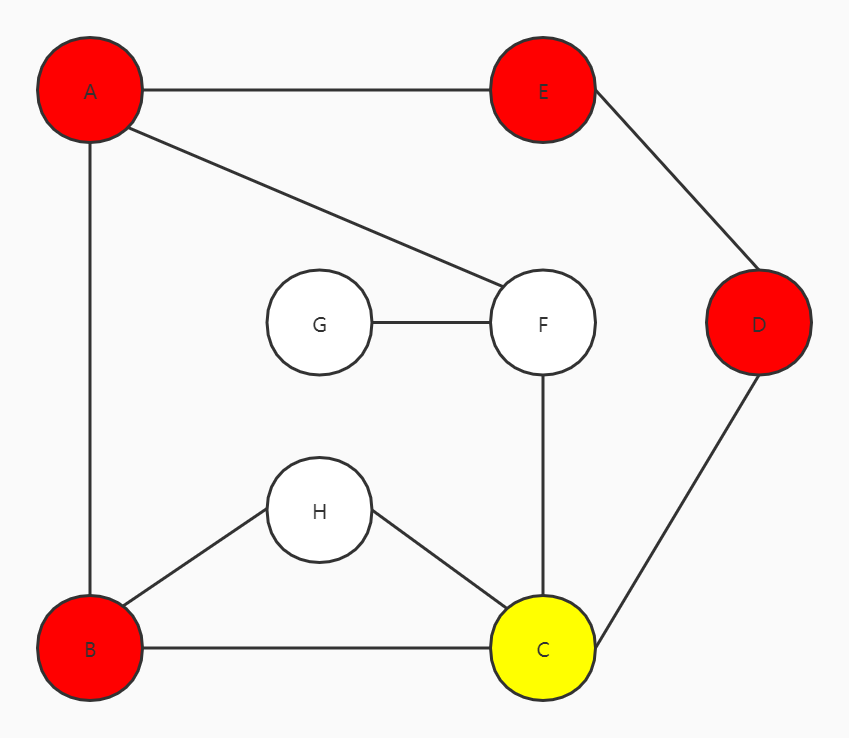
此时C的邻接点中，没有访问过的顶点有H和F，往右走到F

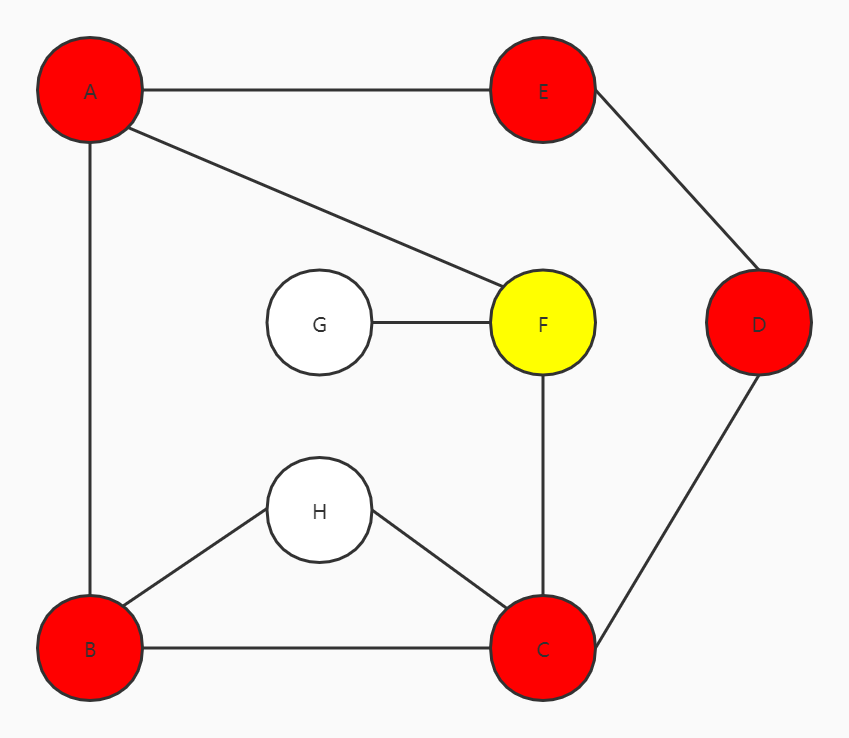
G没有访问过，访问G

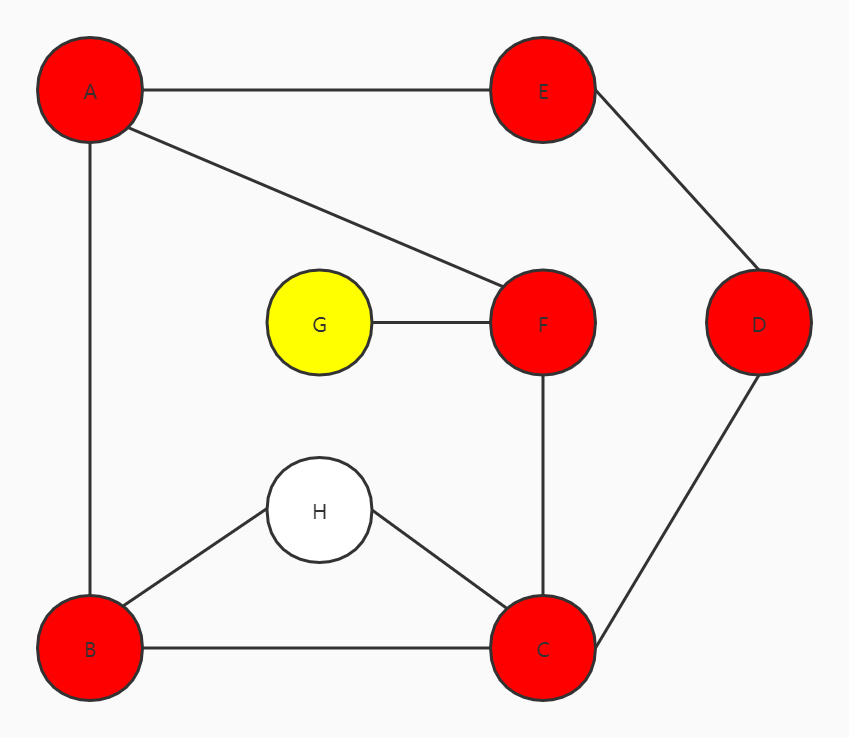
和之前一样，按原路返回，返回到C

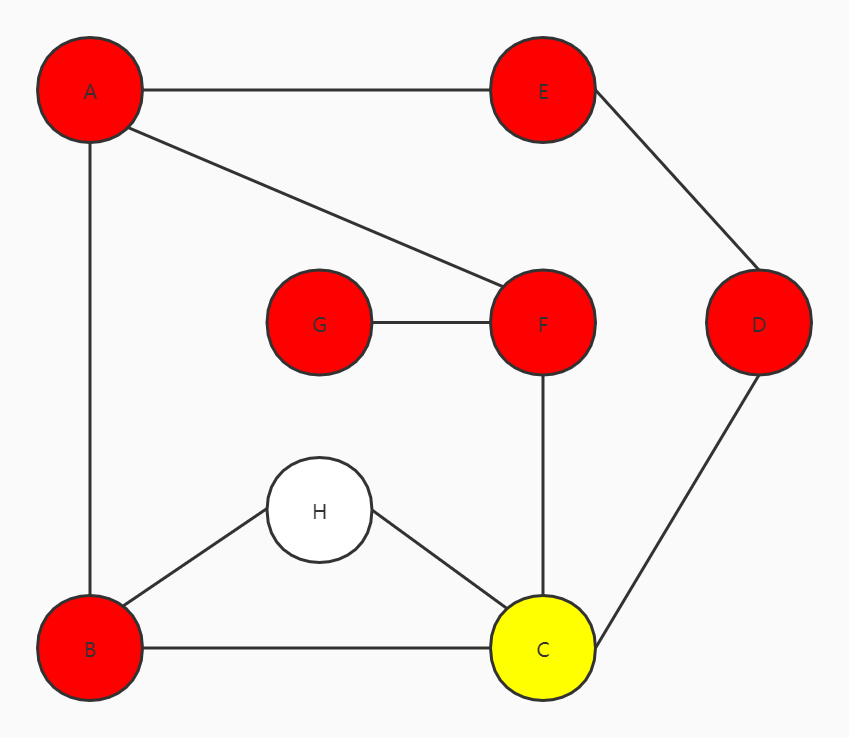
访问H

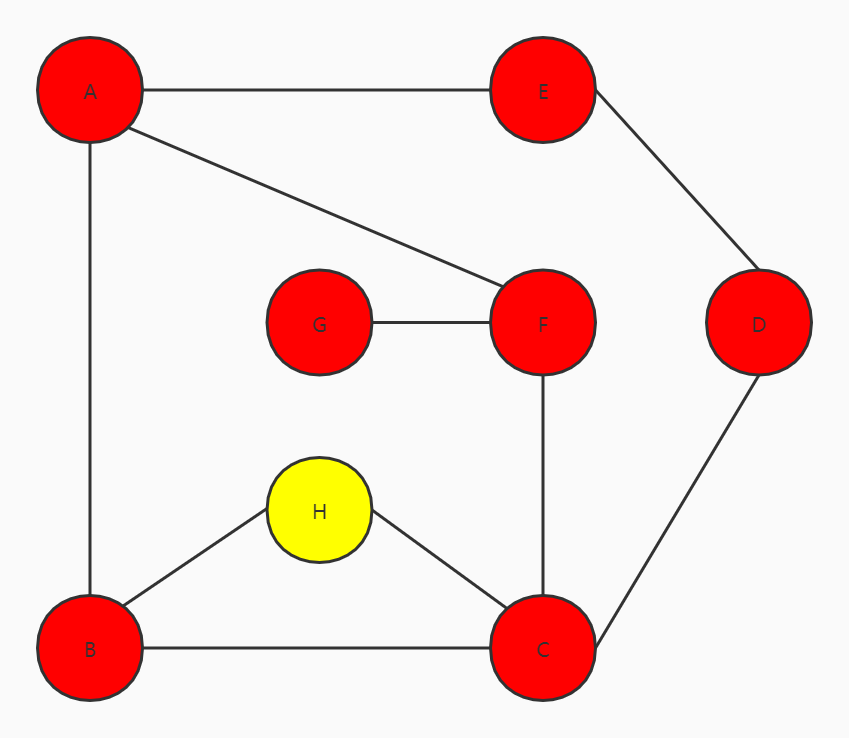
此时图中顶点已全部遍历完成，但并不意味着完成，C、B有可能还有分支，回到A时则表示遍历完成。

DFS的遍历顺序类似与树的前序遍历，从树的形式就可以理解所谓的深度。

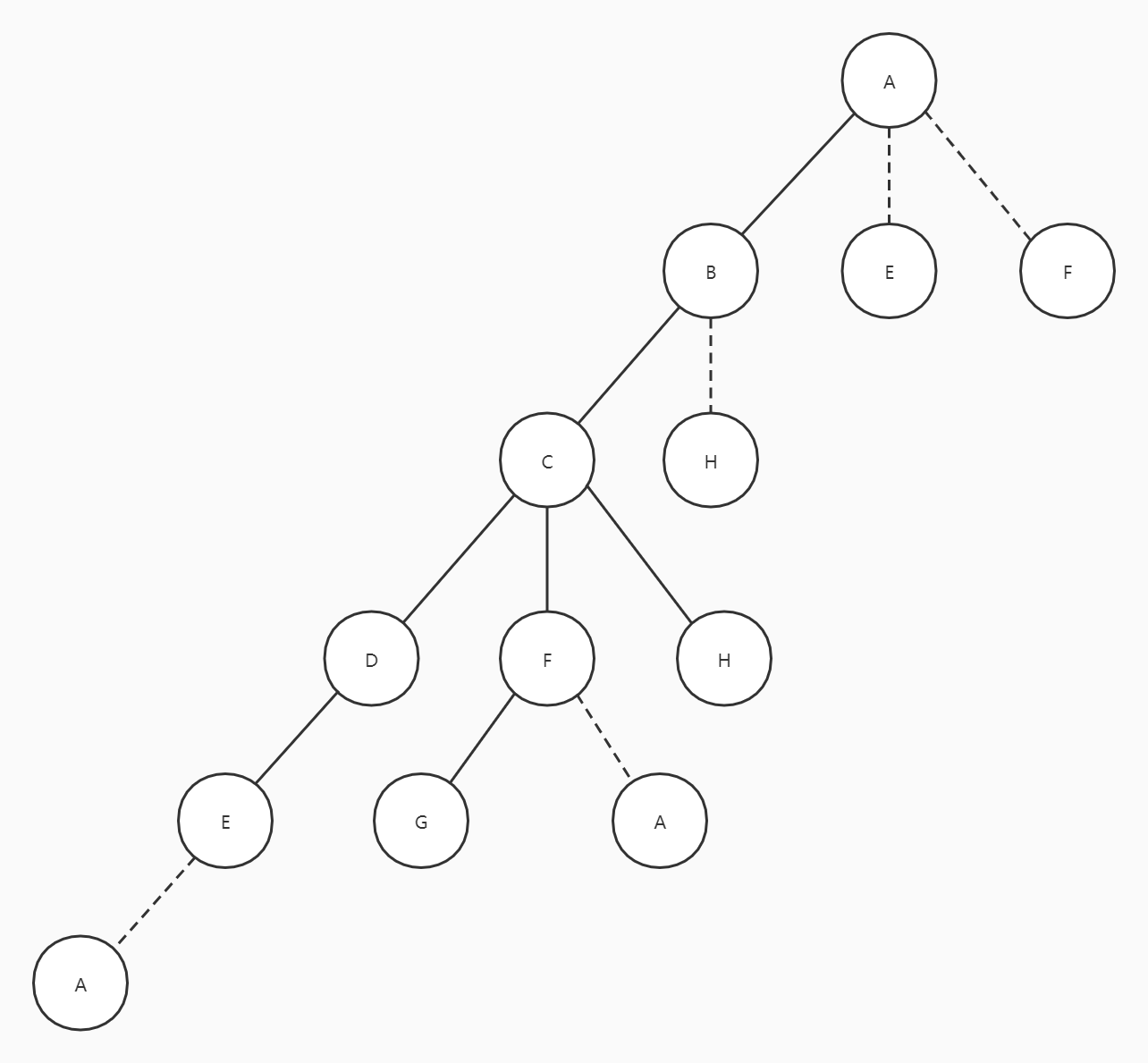
原路返回需要保存之前走过的顶点信息，可以用栈或递归函数来实现

用一个全局变量visited来标记顶点是否走过，visited是一个bool数组

邻接矩阵

void DFS(mgraph* g, int i)
{
    visited[i] = true;
    cout << g->vexs[i] << ' ';
    for (int j = 0; j < g->num_vexs; j++) {
        if (g->arc[i][j] == '1' && !visited[j]) {	//若为邻接点且没有访问过, 递归调用DFS()
            DFS(g, j);
        }
    }
}

对一个存储在邻接矩阵的图来说，找到所有的邻接点需要遍历一整行，这意味着其时间复杂度为O(n^2)

邻接表

bool* visited;

void DFS(lgraph* g, int i)
{
    visited[i] = true;
    cout << g->arr[i].data << ' ';
    arcnode* p;
    p = g->arr[i].head;
    while (p != NULL) {
        if (!visited[p->adjvex]) {
            DFS(g, p->adjvex);
        }
        p = p->next;
    }
}

对于n个顶点e条边的邻接表来说，时间复杂度为O(n+e)

广度优先遍历

Breadth First Search

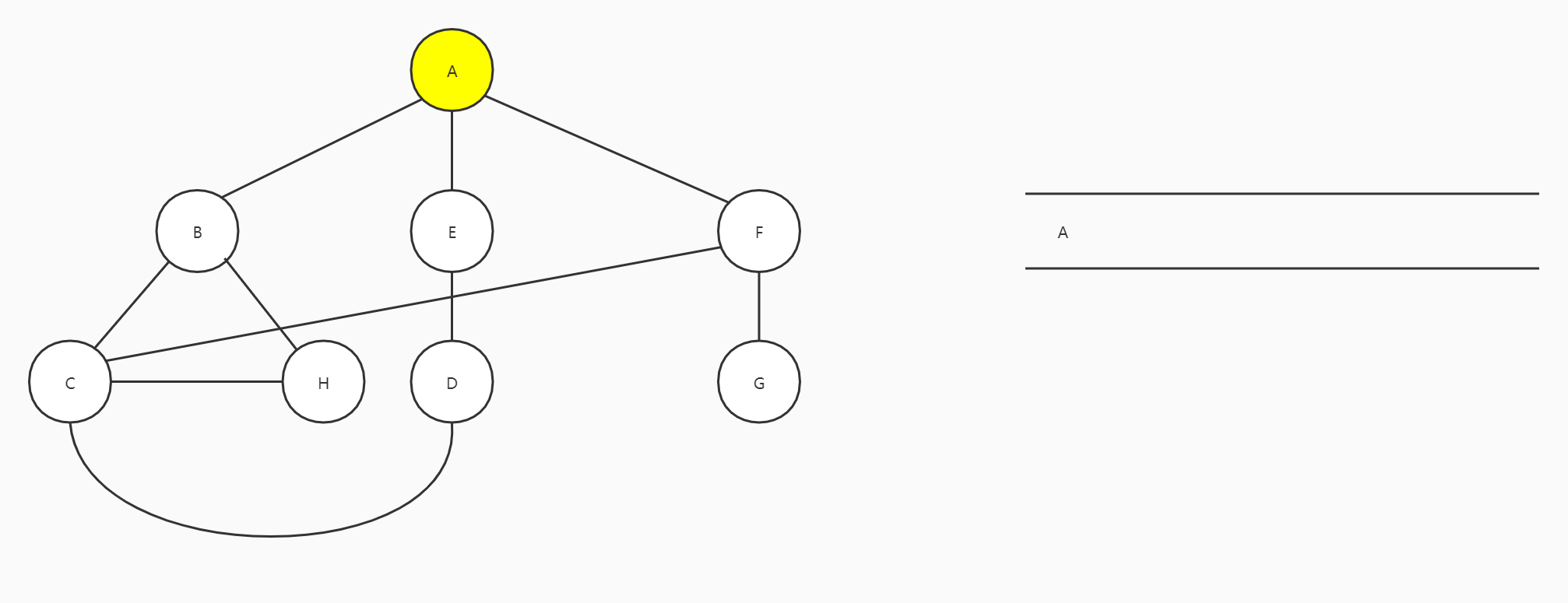
以A为起始顶点，A进队

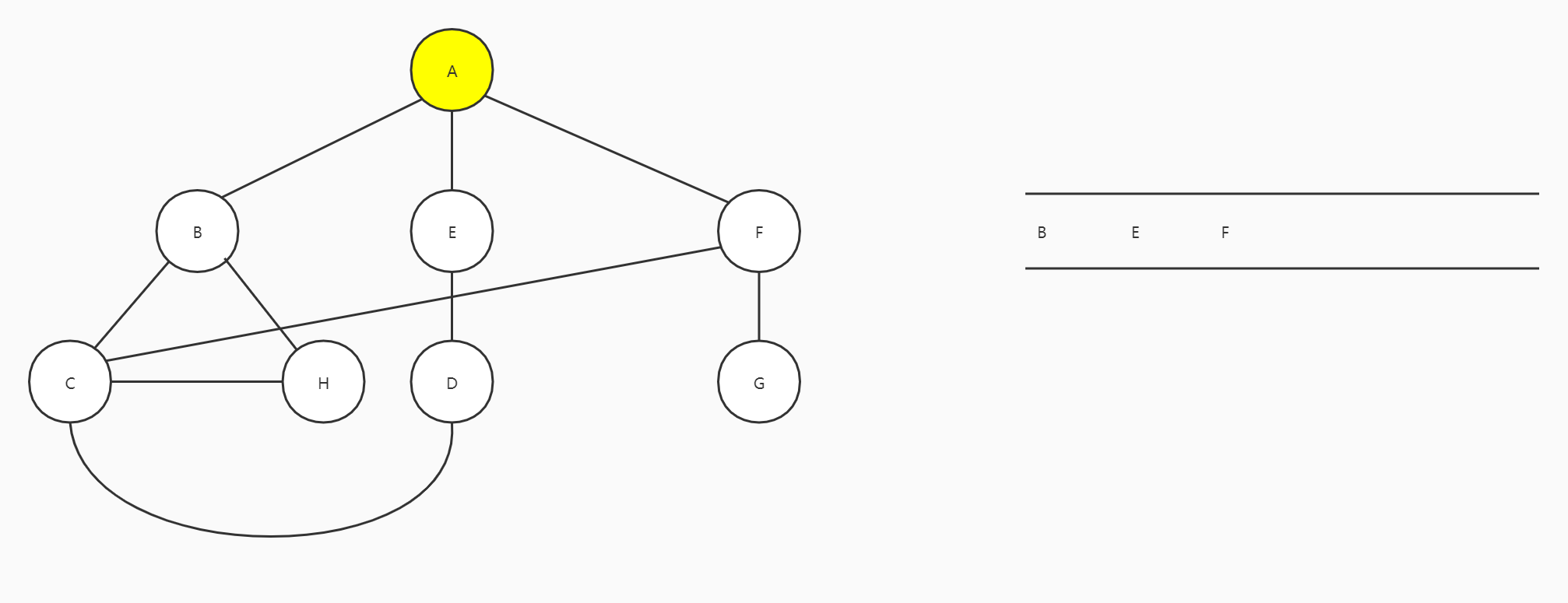
A出队，A的邻接顶点B、E和F进队

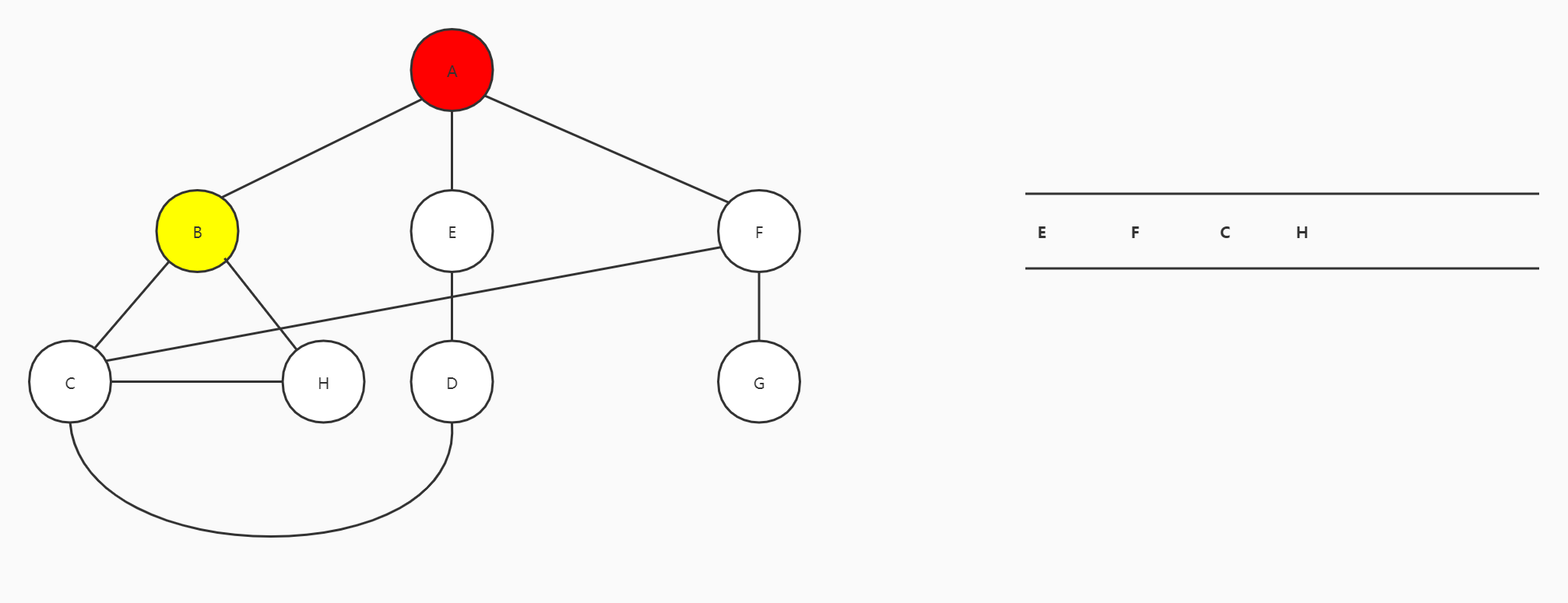
B出队，B的邻接顶点有A、C和H，C和H没有访问过，C和H进队

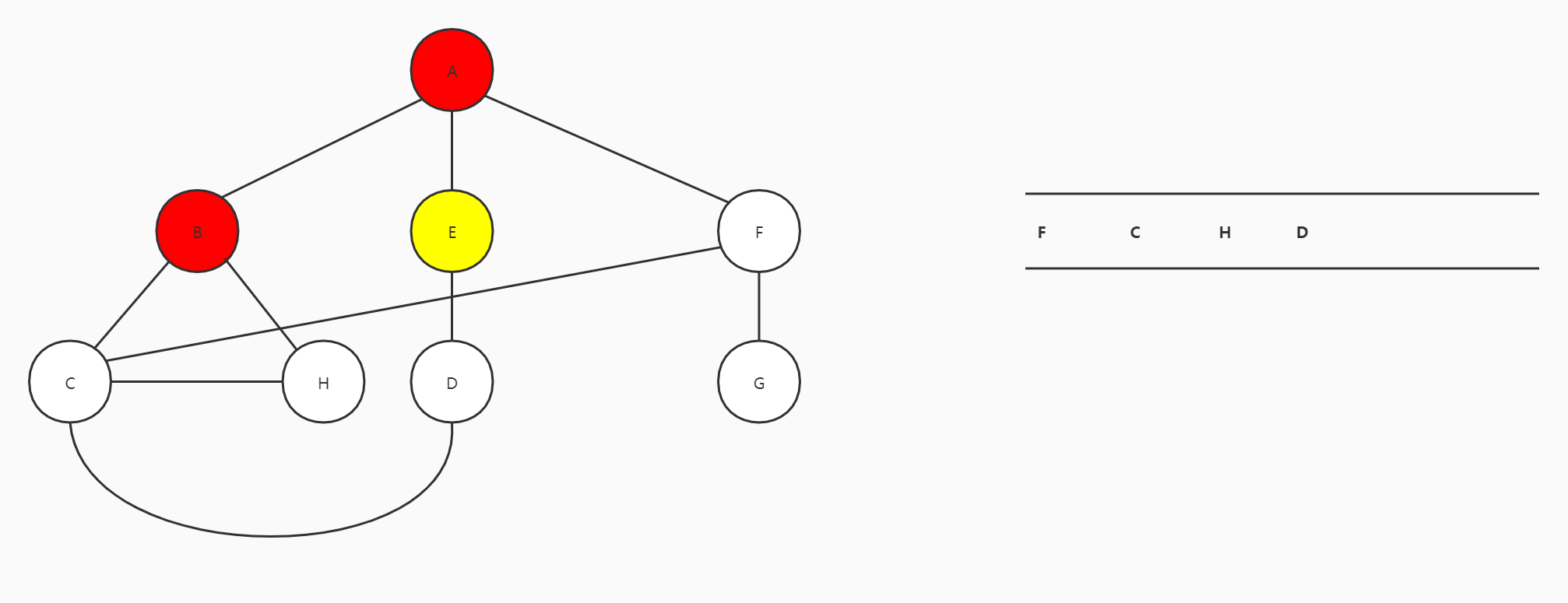
E出队，D进队

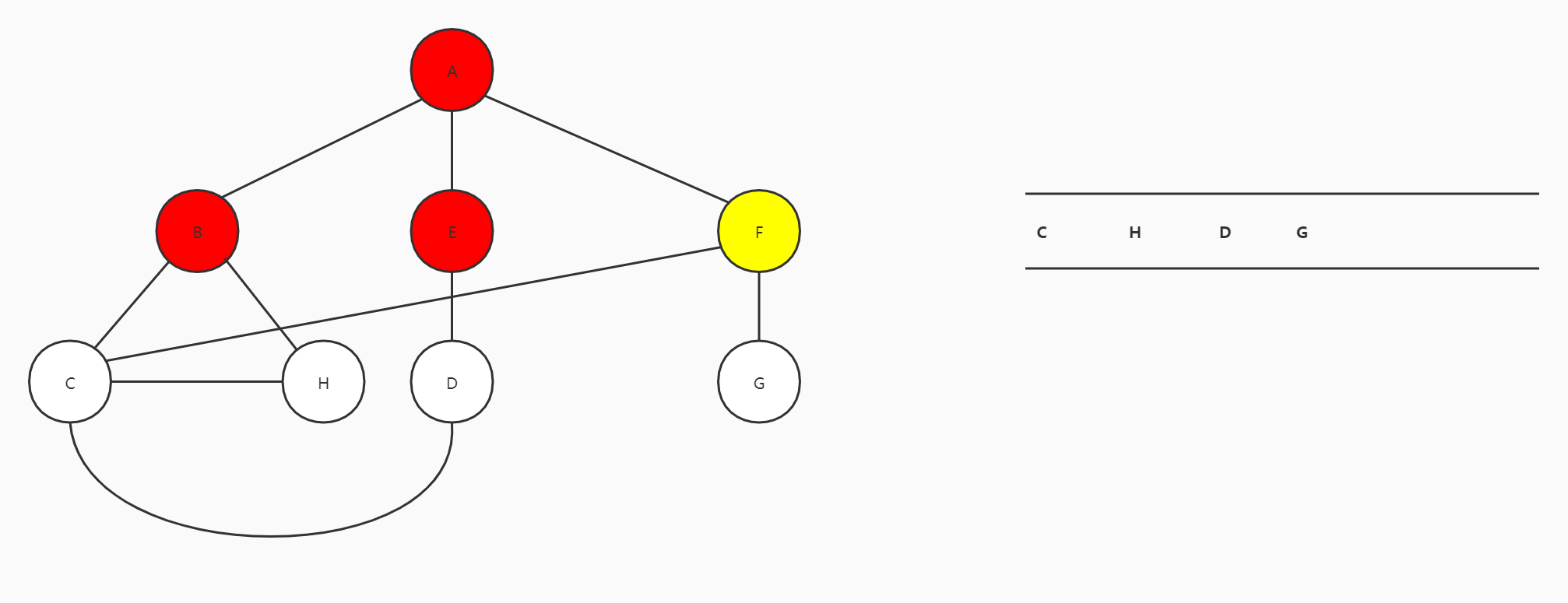
C出队，C的邻接顶点都已经访问过，没有顶点进队

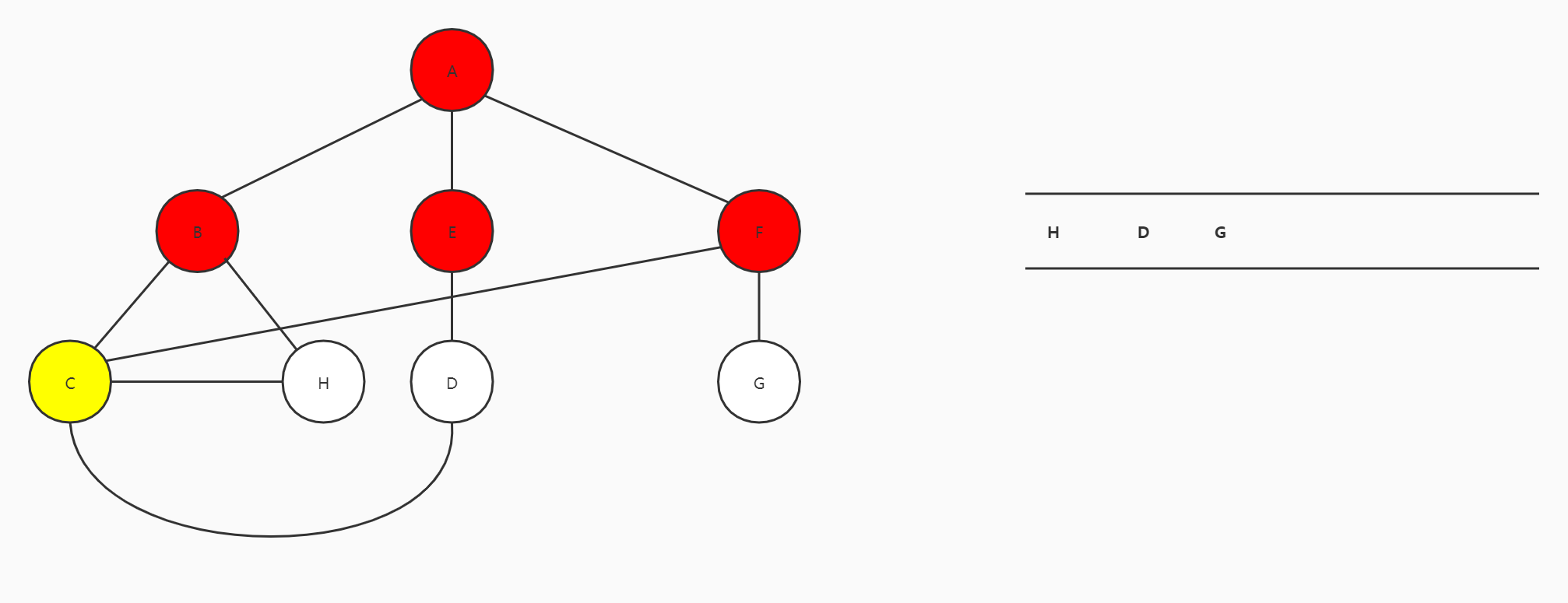
后面的顶点以此类推

邻接矩阵

void BFS_Traverse(mgraph* g)
{
    visited = new bool[g->num_vexs];
    for (int i = 0; i < g->num_vexs; i++) {
        visited[i] = false;
    }
    queue<int> q;					//初始化一个队列
    for (int i = 0; i < g->num_vexs; i++) {
        if (!visited[i]) {
            visited[i] = true;
            cout << g->vexs[i] << ' ';
            q.push(i);	//元素i进队
            while (!q.empty()) {	//队不为空时循环
                i = q.front();		//取队头元素
                q.pop();			//出队
                for (int j = 0; j < g->num_vexs; j++) {
                    if (g->arc[i][j] == '1' && !visited[j]) {
                        visited[j] = true;
                        cout << g->vexs[j] << ' ';
                        q.push(j);	//元素j进队
                    }
                }
            }
        }
    }
    delete[] visited;
}

邻接表

void BFS_Traverse(lgraph* g)
{
    visited = new bool[g->num_vexs];
    for (int i = 0; i < g->num_vexs; i++) {
        visited[i] = false;
    }
    queue<int> q;
    for (int i = 0; i < g->num_vexs; i++) {
        if (!visited[i]) {
            visited[i] = true;
            cout << g->arr[i].data;
            q.push(i);
            arcnode* p;
            while (!q.empty()) {
                i = q.front();
                q.pop();
                p = g->arr[i].head;
                while (p) {
                    if (!visited[p->adjvex]) {
                        visited[p->adjvex] = true;
                        cout << g->arr[p->adjvex].data;
                        q.push(p->adjvex);
                    }
                    p = p->next;
                }
            }
        }
    }
}

非连通图的遍历

在无向图中，若从顶点i到顶点j有路径，则称顶点i和j是连通的。

对于一个无向连通图

• 调用一次DFS()便能够访问到图中的所有顶点

对于一个无向非连通图

• 调用一次DFS()只能访问到初始点所在连通分量中的所有顶点，不可能访问到其他连通分量中的顶点

无向图G中的极大连通子图称为G的连通分量，这个连通子图含有极大顶点数，即再多一个顶点就不连通。

所以，遍历算法需要遍历每个连通分量，才能保证访问到图中的所有顶点

邻接矩阵

void DFS_Traverse(mgraph* g)	//若为邻接表则换参数类型
{
    for (int i = 0; i < g->num_vexs; i++) {
        visited[i] = false;
    }
    for (int i = 0; i < g->num_vexs; i++) {
        if (!visited[i]) {	//遇到没有遍历过的顶点，将其作为新的初始顶点进入DFS()
            DFS(g, i);
        }
    }
}

邻接表

void DFS_Traverse(lgraph* g)
{
    visited = new bool[g->num_vexs];
    for (int i = 0; i < g->num_vexs; i++) {
        visited[i] = false;
    }
    for (int i = 0; i < g->num_vexs; i++) {
        if (!visited[i]) {
            DFS(g, i);
        }
    }
}

调用DFS()的次数等于连通分量的个数

总结

• DFS适合目标明确，比如判断某对顶点之间是否连通的问题
• BFS适合搜索范围会不断变大的问题，比如找出两点之间的最短路径