最小生成树 Prim

最小生成树

Minimum Spanning Tree

最小生成树这个词包含三部分信息

• 树
• 生成树
• 最小

什么是树？

• 树可以看做是一种特殊的图，树没有回路
• 有n个顶点的树一定有n-1条边

什么是生成树？

一个连通图的生成树是一个极小连通子图

• 生成树包含了图中全部n个顶点
• 生成树只有足以构成一棵树的n-1条边

如何得到生成树？

可以通过遍历来得到生成树


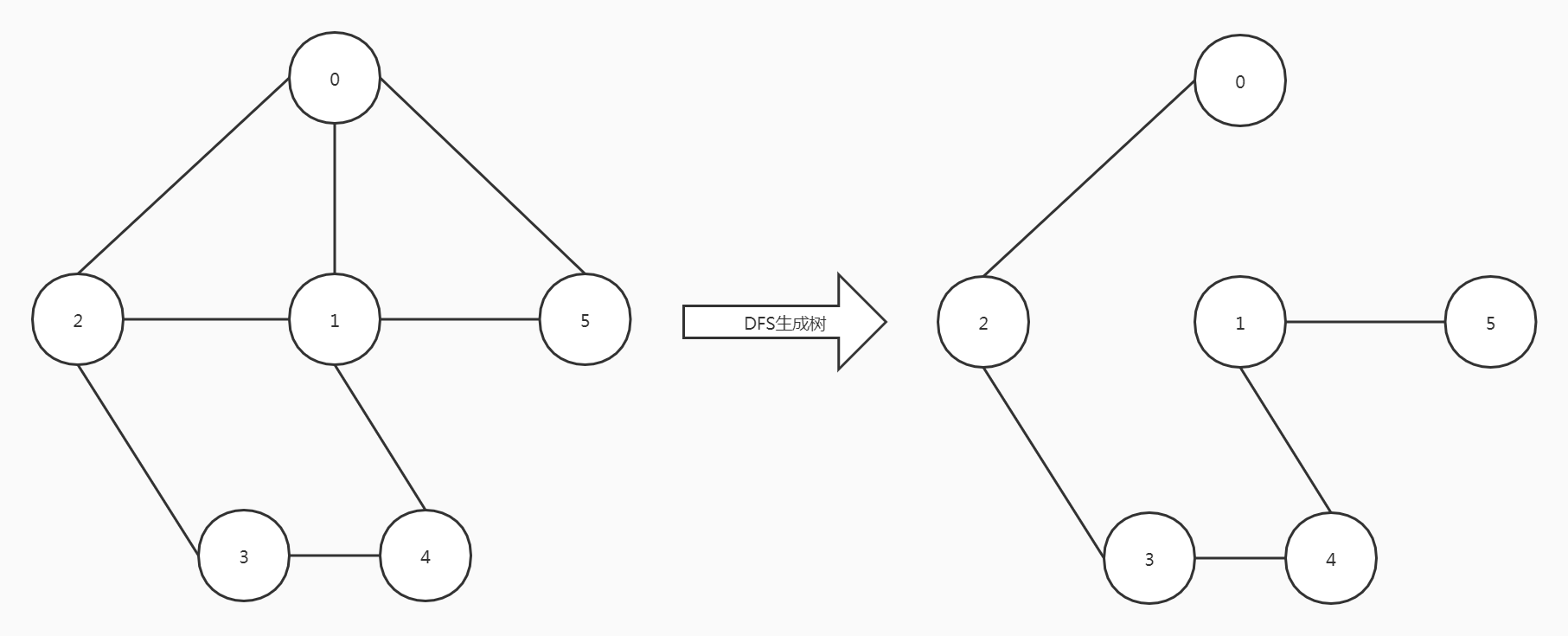
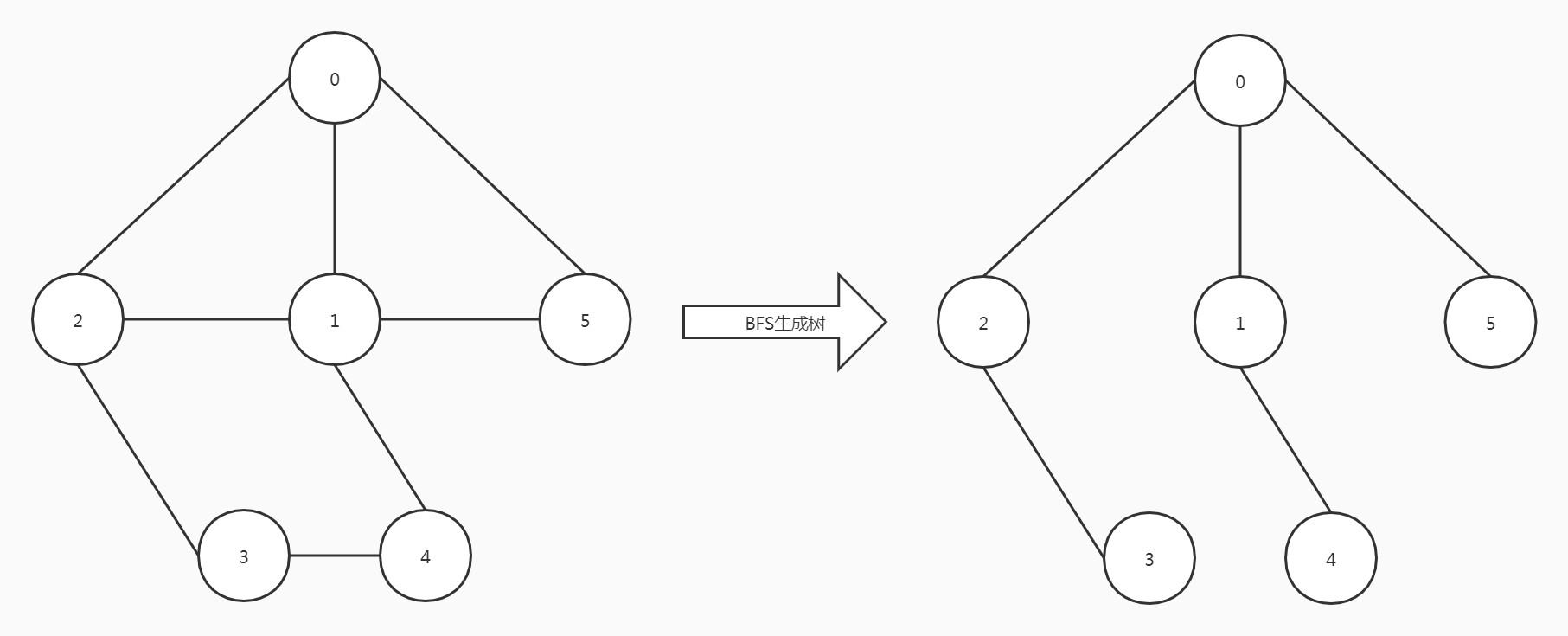
一个图的生成树不是唯一的，可以有多种形式

有n-1条边不一定是生成树，如上图右下角所示。

生成树的性质

• 向生成树中任意添加一条边一定构成回路。
• 一个图若存在对应的最小生成树，则此图为连通图，反之也成立。

什么是最小？

对于一个带权图来说，权值之和最小的生成树就是最小生成树

最小生成树的实际问题

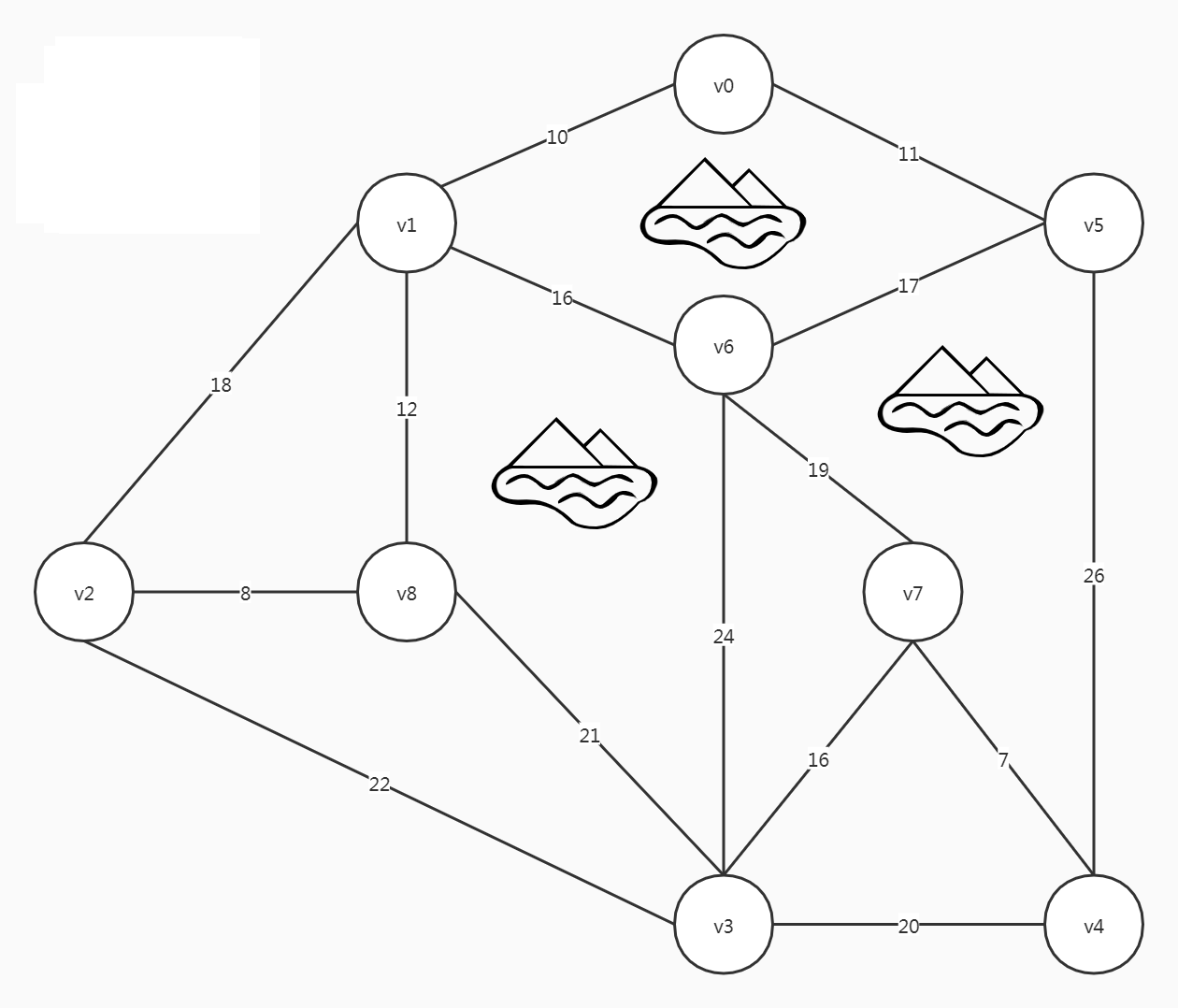
如上图所示，图中一个顶点代表一个村庄，除少数被山川阻隔的路线，村庄之间的距离都以带权边的形式给出，要求你设计一个造价最低的修路方案，把所有的村庄连通。

既然是造价最低，那肯定不是修成像城市那种网状结构。很自然的我们想到了树形结构，当然线性结构算树形结构的一种特殊情况。用计算机来求解，就是图的最小生成树问题这一类问题。

Prim算法

Prim算法的思路是：从一个根节点开始，让这棵小树慢慢长大。

Prim算法是一种典型的贪心算法

什么是贪？

每一步都要是最好的

什么是好？

对于修路的问题而言，当然是选到权重最小的边

贪心得有度，贪心是有约束条件

约束条件

• 只能选n-1条边
• 不能形成回路
  如果选了这条边就会形成回路，即使这条边的权重最小也不能选

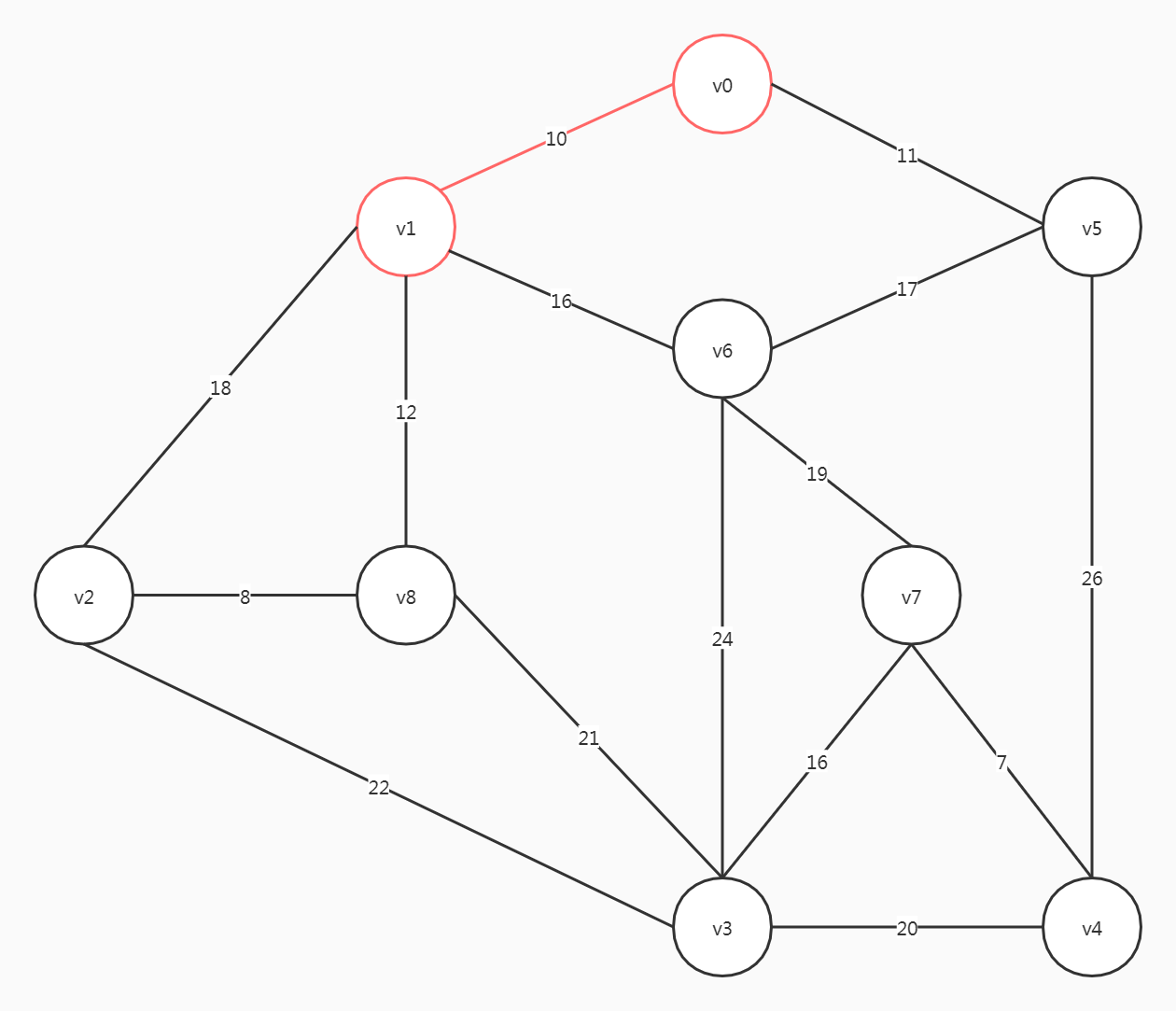
从v0开始

可用的备选边	权重
(v0, v1)	10
(v0, v5)	11

选择权重较小的(v0, v1)

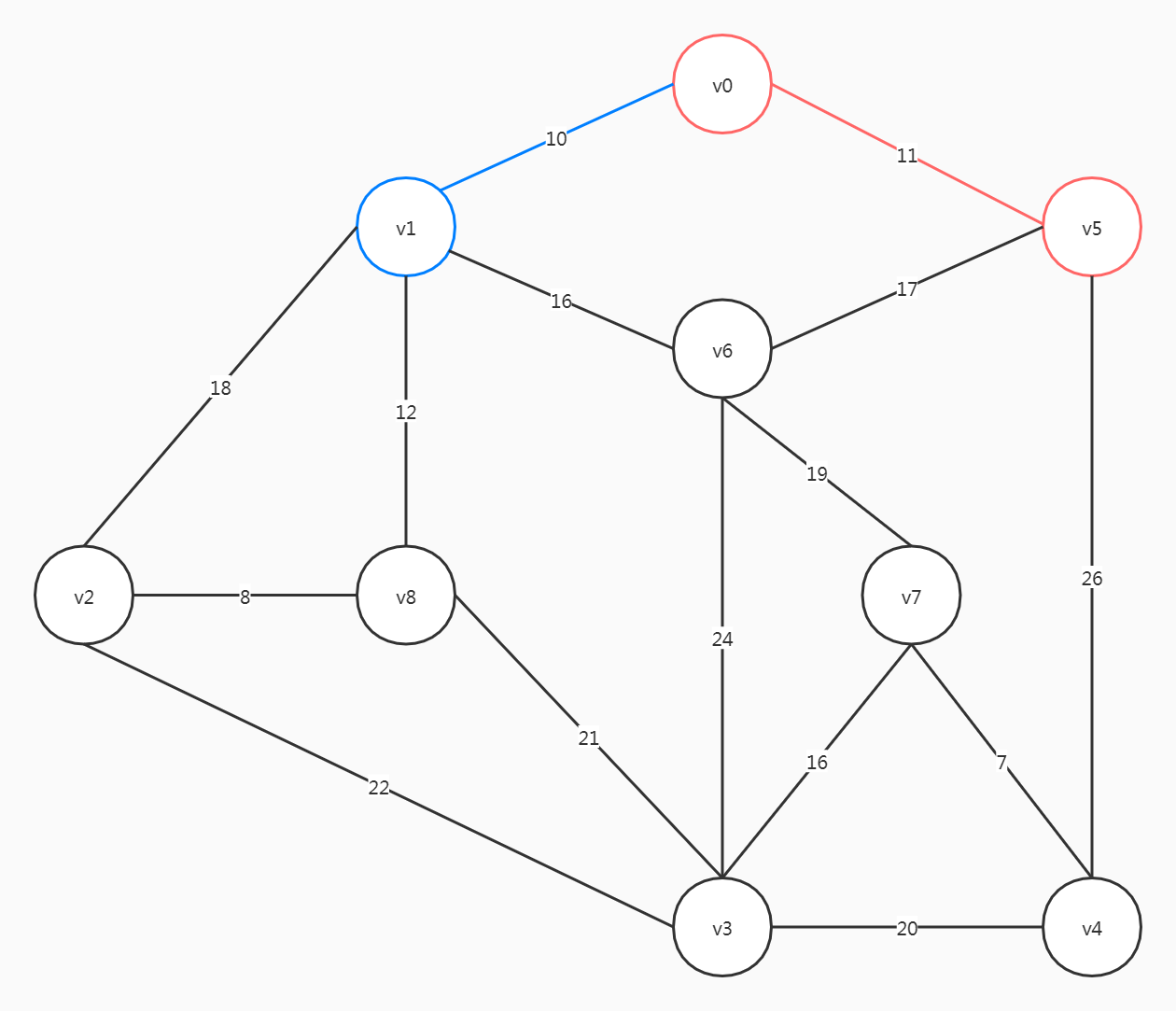
可用的备选边	权重
(v1, v2)	18
(v1, v8)	12
(v1, v6)	16
(v0, v5)	11

选择(v0, v5)

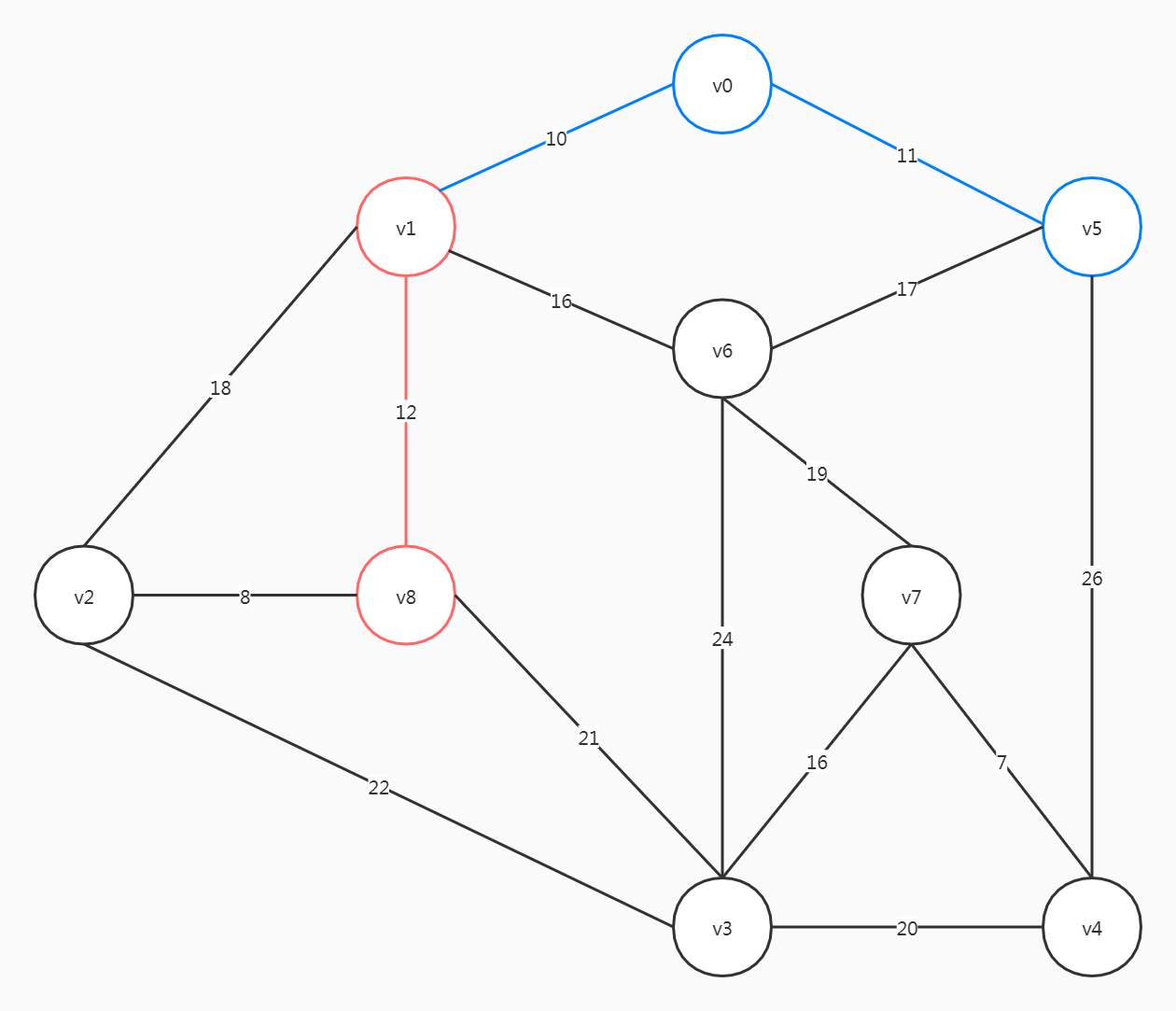
选择(v1, v8)

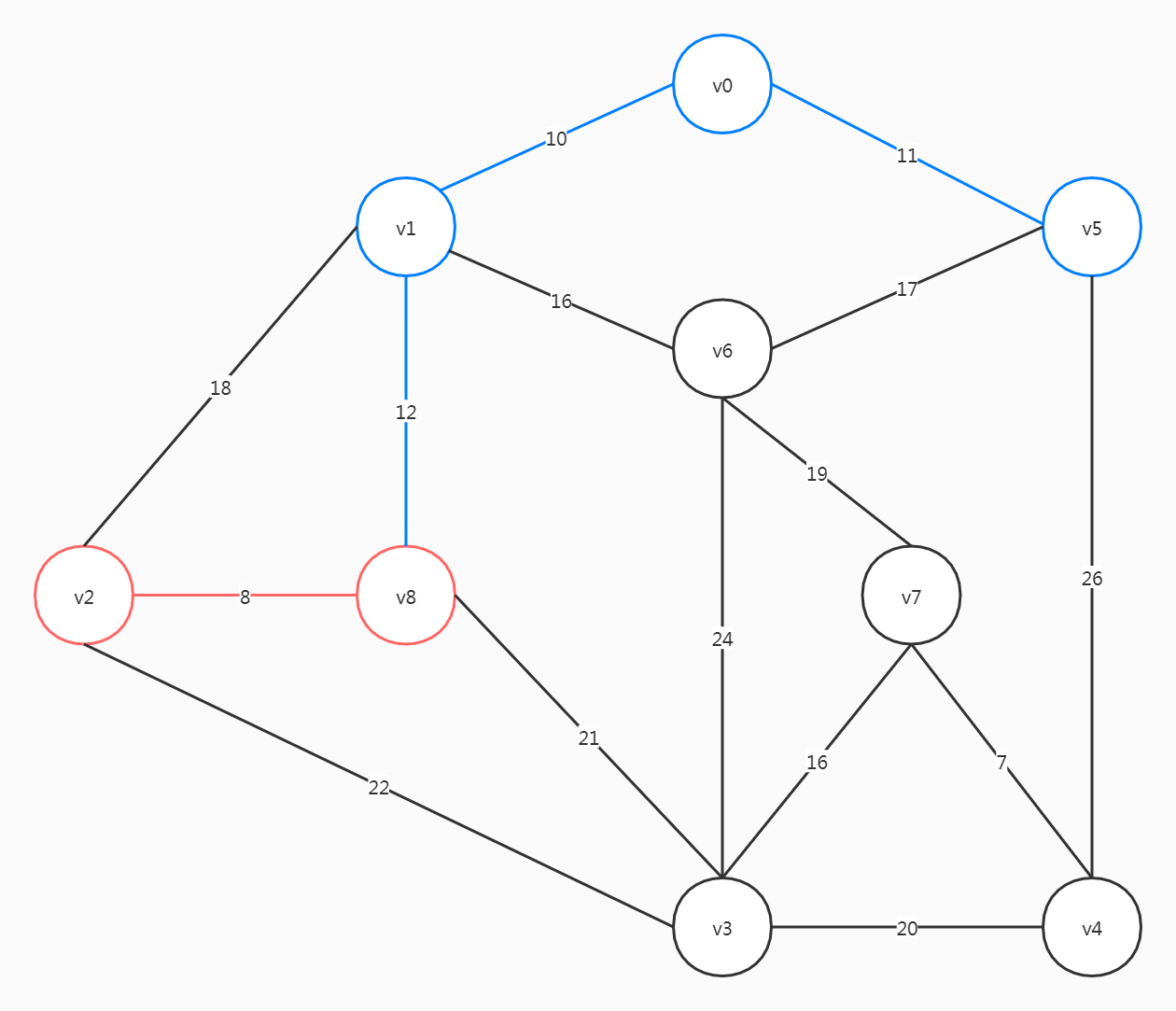
选择(v2, v8)

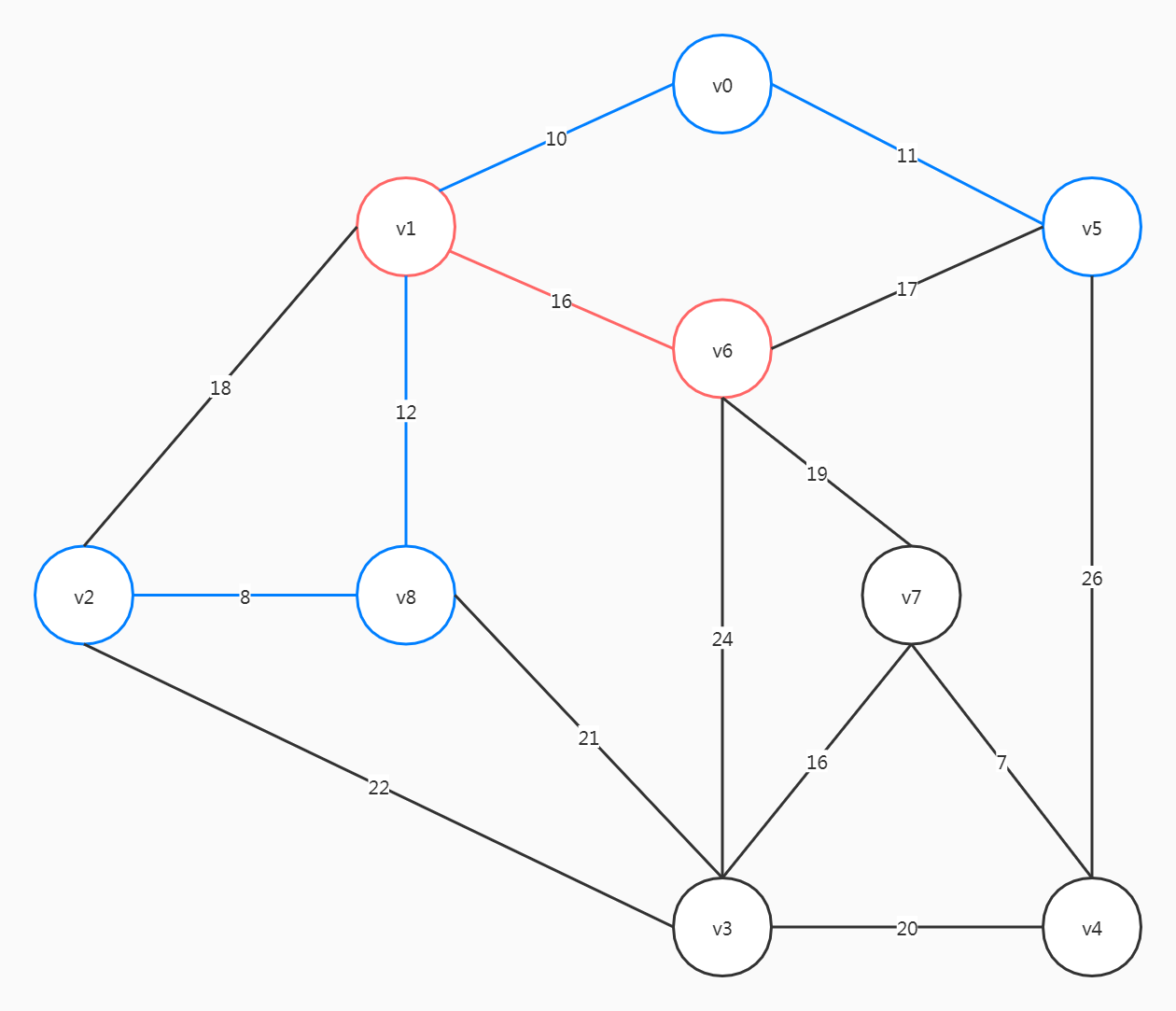
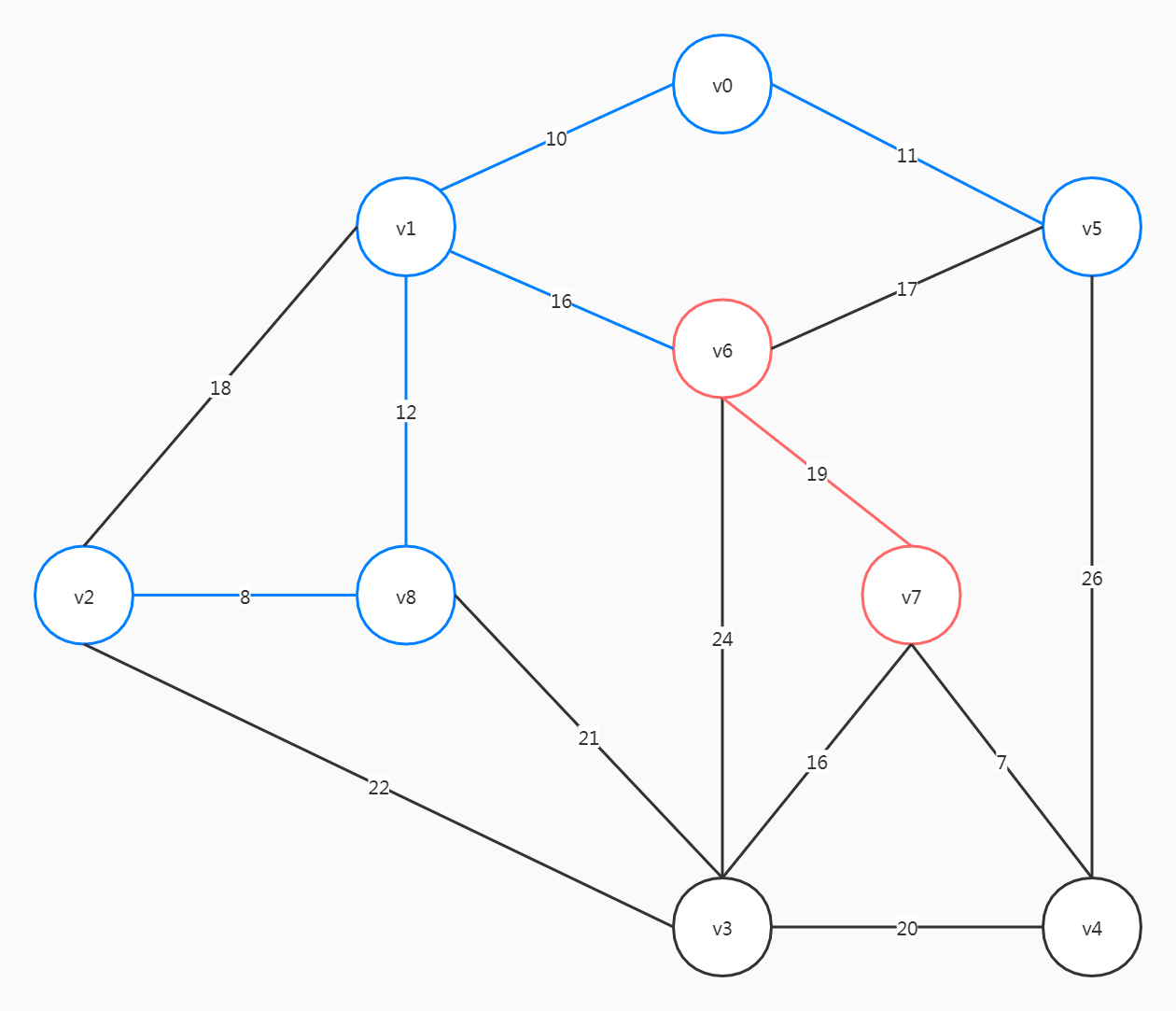
这里需要注意，选择了(v1, v2)之后会形成环，(v1, v2)不能选择。
同理，(v5, v6)也不能选择。

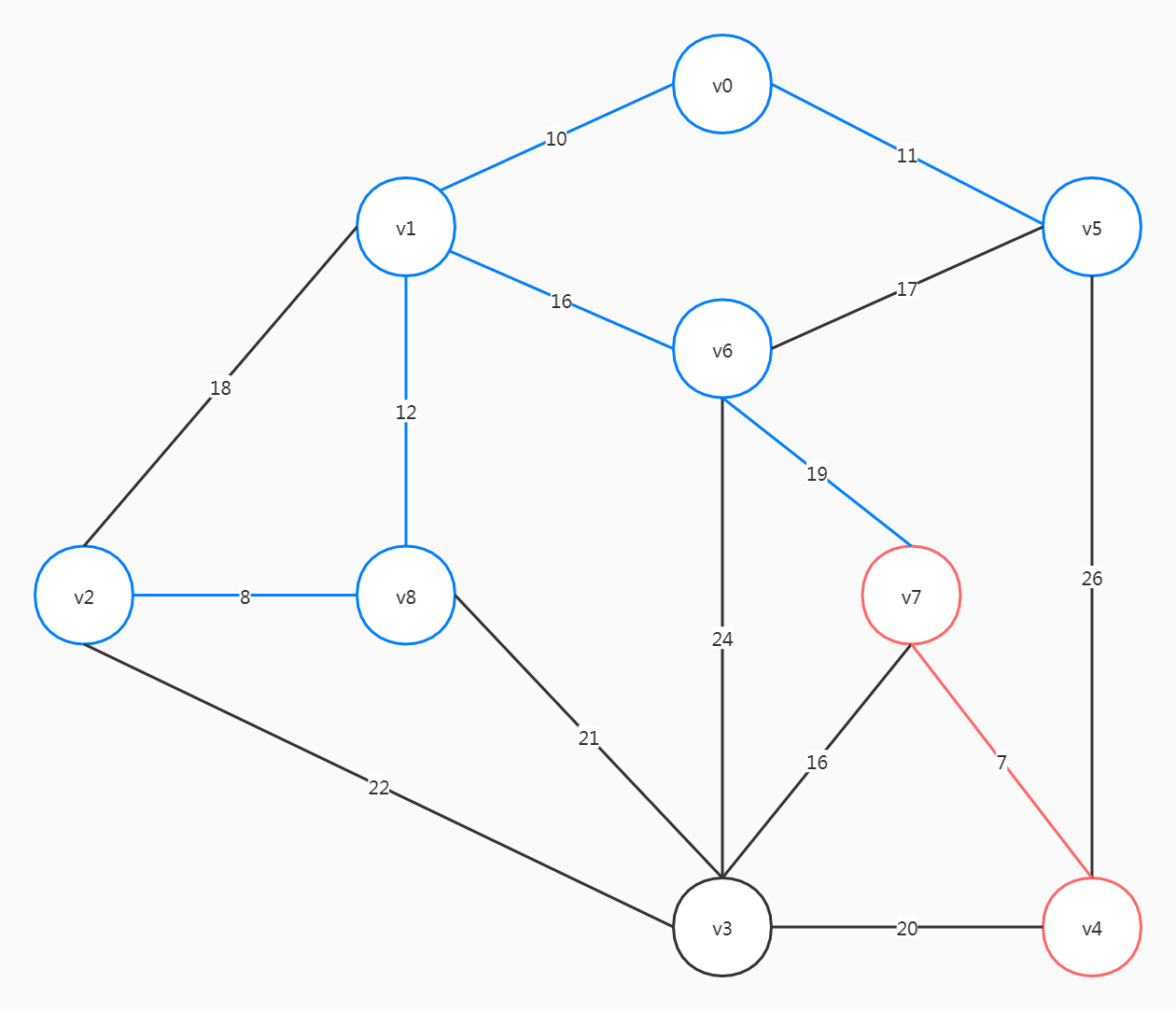
选择(v7, v4)

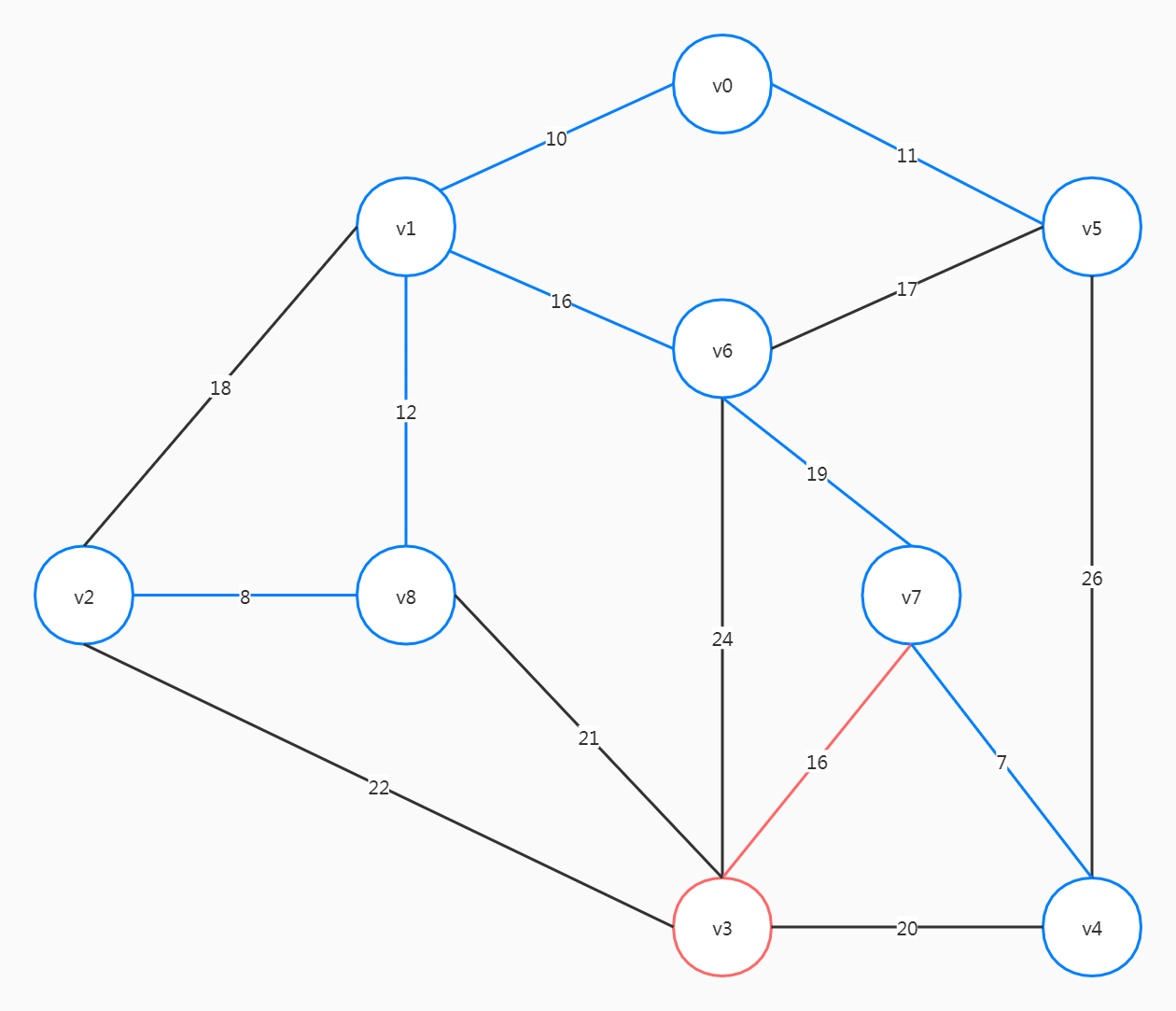
选择(v7, v3)，最小生成树建立完成
$$权重和=10+11+12+8+16+19+7+16=99$$

下面来看代码实现

建立邻接矩阵

typedef int   VertexType;
typedef short ArcType;

以单字有符号数能取到的最大值32767为∞

输入

9
0       1       2       3       4       5       6       7       8
0	    10	    32767	32767	32767	11	    32767	32767	32767
10      0	    18  	32767	32767	32767	16	    32767	12
32767	18  	0	    22  	32767	32767	32767	32767	8
32767	32767	22	    0	    22	    32767	24	    16	    21
32767	32767	32767	22	    0	    26	    32767	7	    32767
11	    32767	32767	32767	26  	0   	17	    32767	32767
32767	16	    32767	24    	32767	17	    0	    19  	32767
32767	32767	32767	16	    7	    32767	19  	0	    32767
32767	12	    8	    21	    32767	32767	32767	32767	0

void MST_Prim(mgraph* g)
{
    ArcType* lowcost;   //存储权值的数组
    lowcost = new ArcType[g->num_vexs];    
    lowcost[0] = 0;     //以v0作为小树的根节点

    int* adjvex;
    adjvex = new int[g->num_vexs];
    adjvex[0] = 0;

    for (int i = 1; i < g->num_vexs; i++) {
        lowcost[i] = g->arc[0][i];  //将那些和v0邻接的边的权值放进数组里 (不邻接看成邻接但距离无穷大)
        adjvex[i] = 0;              //初始化这棵树只有v0一个节点
    }

    int min;    //一定范围内的最小权值
    int min_k;  //存储最小权值的顶点下标
    const ArcType Inf = 32767;  //权值的无穷大

    for (int i = 1; i < g->num_vexs; i++) {
        min = Inf;
        min_k = 0;
        for (int j = 1; j < g->num_vexs; j++) {
            //在lowcost里面找到权重最小的边
            if (lowcost[j] != 0 && lowcost[j] < min) {  //lowcost的元素为0则表示该顶点已纳入MST中
                min = lowcost[j];
                min_k = j;
            }
        }
        cout << adjvex[min_k] << ' ' << min_k << endl;
        lowcost[min_k] = 0; //将该顶点纳入MST中

        for (int j = 1; j < g->num_vexs; j++) {
            if (lowcost[j] != 0 && g->arc[min_k][j] < lowcost[j]) {
                lowcost[j] = g->arc[min_k][j];  //较小的权值存入lowcost相应位置
                adjvex[j] = min_k;  //这条较小权值的边的其中一个顶点, 在MST中已有的顶点, 存入adjvex
            }
        }
        //把lowcost和adjvex准备好后, 进入下一轮循环后遍历lowcost输出顶点对
    }
    delete[] adjvex;
    delete[] lowcost;
}

算法的时间复杂度为O(n^2)

输出

0 1
0 5
1 8
8 2
1 6
6 7
7 4
7 3