NOI前各种Idea总结以及各种文本乱堆

转载请注明原文地址：https://www.cnblogs.com/LadyLex/p/9227267.html 

不过这篇的确没什么*用了转转吧

2018-6-24 关于一类延迟标记（来自UR14 思考熊）

有的时候我们需要用分块/线段树（即扩展的二进制分组）维护一些末端插入的信息，

当某一块插满之后我们做一个统计答案的操作，这个统计的复杂度较高

但是这样由于复杂度是均摊而无法支持删除

这样的话 我们可以维护一个bad标记，表示当前块的信息是不对的，一开始所有块自然都是bad的

以分块为例，当我们插满一个块的时候，如果前驱块是bad的，我们重建前驱块，移除其bad标记，否则什么也不做；

当删除的时候我们给当前块打上bad标记

查询如果是bad就暴力查询，是好的就用之前处理的答案

这样的话，整块中同时最多有1块是bad的（算算最后没有插满的是2块），所以复杂度是正确的

2018-6-26

发现了一个很巧妙的式子，具体说是“考虑组合意义”的妙用

原题是这么个东西：

在某一步推式子的时候用到了

$$\sum _{d_{1}+d_{2}+...d_{n}= n} \frac{ A _{i} ^{ d_{i} } }{\prod d_{i} !} ==\frac{ ( \sum A_{i} ) ^{K} }{ K! }$$

其实是对组合数的变形 原始式子是这样的：

$$\sum _{d_{1}+d_{2}+...d_{n}= n} \frac{K!}{\prod d_{i} !}A _{i} ^{ d_{i} } == ( \sum A_{i} ) ^{K} $$

2018-6-26 ：关于斯特林数

***一个比较巧妙的应用就是关于通常幂和下降幂的转化

https://blog.csdn.net/owenowl/article/details/79442341

***推式子tricky的地方

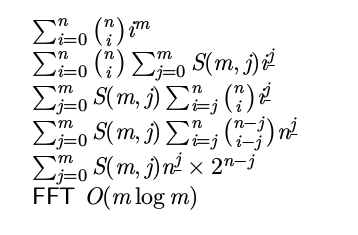
***关于组合意义&统计答案套路的地方：

如果答案是什么个数的k次方，对于拆下降幂那个式子，

组合意义是说每一种方案贡献$S(k,i)*fac(i)$

所以我们求个数为i的方案数$f(i)$，用$f(i)*S(k,i)*fac(i)$来统计答案 

***以及一个不知道干什么的式子

2018-6-26 NOI前要做的事情？

刷一下UNR1,UNR2 以及NOI2016 & NOI2017

然后继续做UR的过程……个人感觉UR的题目质量都非常高

学新东西就不了……不开新的知识点了……

找个时间回看一下之前记的笔记们，别忘了之前学的家伙……

然后重新开始坚持每天写总结，另外现在pdf上附赠的讲题也挺好的，要看看

2018-6-27 关于浮点数的精度

之前听别人说什么double的精度比longdouble好

似乎并不是这样 上午的T2我double的时候wa 开了longdouble之后就能过 因为这个挂了41分

longdouble内存是12字节的，使用的时候精度要比double8字节高2到3位

并且longlong和double之间的转换可能会出问题，但是和longdouble之间似乎不会出问题

为了避免这样的傻逼情况

首先能打精度高的打法就不要用精度折磨自己

然后就多用用longdouble……

2018-6-27 关于根号分类

今天又被根号分类焦作人了，感觉自己菜爆……

这个思想非常的妙，看了一下提交记录，liu_runda老先生在考场上就想到了

根号分类，可以是“在数据范围中，有一些变量的乘积有约束，比如”长度大于$\sqrt(n)$的串不超过$\sqrt(n)$个“，然后采用数据分治

也可以是”元素个数大于$\sqrt(n)$的集合不超过$\sqrt(n)$个“，然后对于不同大小的集合采用不同的维护方法

真的很厉害……虽然被这种做法作为正解/高分暴力吊打了很多次，但是我还是想不到啊

其实有很多时候，根号分类的两种方法是两种不同数据范围下的优秀解法，很可能就是俩暴力

也许以后发现那些不管怎样都很难维护的东西就要多想想根号的东西了

以及最近很少看到根号算法（分块莫队之类），应该找时间看看

以及网络流有一段时间没有考过了，过几天可以去看一下”奇怪的线段树“试试

2018-6-27 今天的日记

在昨天一天的练习之后今天重新开始考试了
上来通览之后发现T1部分分很足，T2没思路，T3似乎是比较套路的题
就先开的T3,然后发现自己在60分到AC的倍增优化那里卡住了，式子不对
然后卡题半小时之后扔掉看T1，发现部分分很好打，打了一半发现自己会处理换根的LCA了……然后就可以做了
测大样例发现了一个错误，改过来就对了
然后去看T2,一开始没有什么思路，就开始拼命手玩小样例寻找决策规律
然后推了一个没有任何知识点的单调栈维护凸包+二分查找点值的算法
打完之后调了一下式子过了大样例
然后回去看T3无果，最后就GG了
100+59+59 RK2
成绩看上去不错，但是个人觉得是能占小小的优势原因是，
题目没有达到让人绝望的难度，大家能想到的都差不多是3正解
自己走了一点运气，能想出T2的做法才能占优。
然后两点半改完题之后复读鸡xn，
两个多一点小时的时间都在讨论如何使用整数二分的方法
以及给同学们讲解T2的做法，然后发现我和题解切入点丝毫不一样……
接着看了UOJ309这道题
40分暴力卡了我半个小时调试，最后发现是“平移一行”的时候可能平移到自己，然后这时我的智障操作就会把它变成0
这样的细节问题真的要注意，如果因为这样的小问题丢分就太傻逼了
然后一点小小的总结……
屡次考试得出的结论是，我只有中低档题/见过的套路题才能拿较高的分数，
能快速切掉一题才能保证三题都是正解+高分暴力，rank才能靠前，但是NOI并不送分
而且NOI也不可能让我三题都是正解+高分暴力
并且我觉得个人也没有特别强的某一个专项，属于比较平庸的普通选手
这样的话只能发挥自己仅有的一点小优势了
什么优势呢…………似乎没啥优势，毕竟自己并不天赋过人，也没有超常的努力
所以只好趁着有机会，再做做自己能做的了，保持正常状态，不要颓翻不要浪翻
平心而论自己并没有把该做的做的多好，所以并不敢说“把自己能做的做到最好”这样的话。
引zyfblog中的话：“不管是怎样的回忆，都是我们活过的人生。”
NOI，加油吧。

 2018-6-28 继续关于根号分类

怎么我昨天被根号吊打今天还没有记性啊23333

在涉及到约数个数，质因子个数等等东西之后，我们也可以采取根号分类的方法

比如说”一个数只会含有一个大于$\sqrt(n)$的质因子“

这个常用于一些dp方向的题目，比如最典型的是noi2015寿司晚宴

还有就是动态fwt的那个点子

如果我们需要动态修改一个高位前缀和数组，我们可以考虑分块维护：用二维数组$f[i][j]$表示“前面$\frac{n}{2}$维大于等于i，后$\frac{n}{2}$维恰好为j

这样的话，我们把一个数拆成前后两半v1和v2,插入我们就枚举v1的子集，查询就枚举v2的超集，复杂度是$\sqrt($值域$)$的　　

2018-6-28 今天的日记

今天的测试拿了大众分，没什么好说的
但是有两个问题需要特别注意
一个是分数值不值的问题，在想到T2 80分之后我还花了将近1小时的时间去打表
这个非常不值啊 先不说能不能打出来表 用那么长时间去看20分的确是不值
明明一开始想的是“80分就够了”，结果最后还是看了半天
如果用那些时间去看T3的话也许会有些思路，毕竟之前还是看过slink那一套理论的

然后第二个问题
高三宣传板上面写着的提分点，有什么概念模糊点，什么知识记忆点
……觉得不止适用于高考课
昨天给我最深刻的印象是T1由于不会写Pola Ro（这名字看上去还不错233）而不愿意去想正解
清楚的记得当时想着的是“反正我打不出来Pola Ro的话也没有办法拿分……”
结果就是 知识的遗忘让我丢了分
因为板子丢分……我好像没干过这事啊……
接下来一定要复习之前学过的知识点，不要因为忘记了模板而丢掉分数啊

以及不要空想某一题有多么傻逼，还是要仔细看一看的

T3我看了一下数据范围发现十分大，没有什么好的思路 所以打了个10分暴力就赶紧跑了

考完试发现……挺傻逼的，就是几个板子放在一起了

如果使劲想想，想到了slink以及对应的那个区间加的话这题就没啥了

不过不管是离线维护答案还是slink对于区间的巧妙贡献我都没有想到

所以就算再毒也要看一看每道题

2018-6-29 需要回看的考试题
2-C
3-A
3-B
NEYC4-B
NEYC5-C
NEYC6-B
NEYC6-C
NEYC7-B
NEYC7-C

2018-6-29 离线之后枚举一个端点，维护另外一个端点的答案
似乎是对多组区间询问/全部区间询问的一种优秀解题思路
最近做的不少题都是这样的，但这必须要求答案可以动态的维护
需要观察所求的东西……

2018-6-29 最优化问题是可以用次优解更新答案的，并且这就是所谓的DP……吧……
完了我DP入门都没入门
很多时候我在做最优化问题是都会陷入一种误区，就是想找最优的决策点直接更新答案
但是事实上，我们可以允许不优秀的决策点来更新答案。
如果所有可行的决策点都更新了答案，那么我们肯定可以拿到最优解。
但是要注意的是，所有的决策点必须是可行的；或者，不可行的决策都是绝对的劣解
比如树上最短链，我们可以允许某条路径的两条边来自同一个子树：
这虽然是不可行的决策，但是这一定更劣，我们去子树里就能找到更优的解。
但是如果是最长链就不行了，这样可能会比真正的解更优，从而让我们得到错解
NEYC7B以及UR13B都是这样的题，我们拿所有可行的解去更新答案，得到的就是真正的答案
其实今天上午做UR13A的时候用到了这个思路：
如果我知道了过每个点最长区间的最小值，这就是能达到的最长区间
但是我用的的确不够熟练
这种通过遍历所有决策点而达到最优解的想法是需要巩固的

2018-6-29 接下来复习日的安排（尽可能用考试的晚上找对应的资料）
1.DP优化&DP脑洞专练
2.NOI真题
3.UNR练习
4.多项式各种应用的模板，PolaRo模板……等等模板复习

2018-6-29 今天的日记

今天没有考试，做了一下题……
UR13A，自己想到了90分的数据结构，当时我想的是枚举跨过每个1的最长长度取min
这样我必须找到左右值最小的1的位置
但是正解考虑的是删除每个0时需要用的最长长度取min
这样只需要找到左右第一个值比它小的位置，这样就可以推出正解的结论：
我们从大到小考虑，如果一个点的区间与比他大的点的区间有交，那么只能是包含关系，因此不会更优
所以每个点只会被访问1次，复杂度就变成线性的了
这种两种思路其实差不了多少，但是结果就不一样了
但是这题那10分的思考难度……我觉得有得有半小时，考试的时候如果用这个时间去看另外两题性价比应该会更高
UR13C，看起来就像是min25筛
当然，的确是min25筛，一开始我在想正解那个背包应该怎么处理，
然后发现这样等价于与所有更大的质数互质，就不会做了……
然后后来又想了下，我可以直接枚举每个可以作出贡献的数，
然后或者乘上1个更大的质因子，或者乘上同一个质因子很多次
这个和min25筛的边界限制可以兼容，都是乘积与N的关系
这两题都没有那么难，但是我觉得UR13B的画风非常怪
这就是那种我完全没有思路的简单题
感觉自己的DP学到现在了还是不行，思维不够灵活，只能记一些模板和套路（虽然昨天还被模板卡了）
最近都没有做到那种经典考思路的最优化DP题
都是什么奇怪数位DP，奇怪FFT，树归都不是很多
自己的DP能力本来就不行，最近还在倒车……
接下来应该着重复习一下DP的内容
大概两方面，一个是思路题开脑洞
一个就是复习DP优化的方法
比如斜率优化/凸壳/wqs二分
以及决策单调性/分治/CDQ分治
以及单调队列/单调栈
以及数据结构
感觉这些东西如果出成正解的话反正我是想不到的……
就等下一次总结日的时候，重点搞一下DP吧
看看HZOI上面的滚动条
“距离NOI2018全国赛还有：16天，珍惜最后能学OI的日子！！！！”
真的是……到了分秒必争的时候了……

 

2018-7-4 最近几天的日记

这两天没有写总结
这两天都没有考的多好23333
补一下总结，总结一下考试还是挺关键的
我被wq打爆
6-30T1是一道基础贪心+优化
什么“选最多不相交的线段，那么下一个应该是左端点在我右面中右端点最靠左的"
然后题意对长度有要求，我们暴力就枚举每个点作为第一个，然后往后跳就行了
这样这个往后决策的东西是确定的，倍增一下就变成log了
考试的时候在想用树状数组dp，然后发现：自己不清楚相交的定义
然后就把题意想的特别麻烦，以为是什么“在平面内不相交”
结果相交就是没有重叠的部分
我枚举的是最后一段线段，然后他枚举的是第一段线段
感觉没什么差别，但是我没有想清楚相交的问题，然后就反复修改了好几遍，多花了很长时间
T2，个人感觉还可以打，但是我的实现方法太麻烦了
我存了每个点对应的多项式，然后非要从上往下搞，而维护子树内部然后从下往上搞就清真的多
然后我还以为有个地方我必须用卷鸡，所以我写了个度数方的算法
然后结果发现那其实就是一个sum1×sum2的事情，处理一个prod然后O1乘法完事了
然后正解的转换非常显然，只需要把暴力替换成分治ntt就行了，要写任意模数
考虑到巨大的代码量我考场上就没有打
然后呢……然后我考场上复杂的做法就让我用了大量时间去实现+调试这个题
T3是一个打表然后观察数列性质的题
打出来表之后我并没有观察出任何性质……什么规律都没有找到，只有裸暴力分
最后…………讲个笑话就是我5小时的分数和wq20分钟的分数一样
现在看来，
一场比赛“优秀”，不是说题目水水，也不是说自己能高分屠场很有成就感
一场比赛“不优秀”，也不是说题目太难，根本做不出来
比赛给人的感受，应该最大的影响因素是自己的“参与感”
即使题目非常难，如果自己能打满有效的5h，
即使最后分数不高，排名不靠前，也会是非常让人开心的一次比赛经历
比如说，考试状态良好，没有困的要死，没有饿着肚子，没有半夜着凉……等等
比如说，能够专心的投入题目，不受外界因素（大力敲击键盘）影响
比如说，自己没有犯那些傻逼的错误影响心情
emmmm……说到这个，看看这几天我都干过什么啊
day7T2 由于没加mod而导致输出了负数/没%mod而输出超过mod
day8T1 数组开小100->45
day9T2 FFT的时候写了“w=poww+(opt=1?0:len)”这种代码
day10T3 YY了奇怪的矩阵乘法，没有去实际验证，就死了，感谢只挂了5分
练习的时候做蔬菜，数组各种开小，还有什么“sum=sum+val(应该是sum+size*val)”，
挂到28分，要是考场就直接死了
比如说，时间分配合理，不会出现出考场大骂自己没有看XX题真是sb的情况
day9的T3在看了题解之后发现非常简单，由n5暴力dp直接就能一步步优化成正解
但是考场上全去打T2了，T3没有时间了
比如说，能够打出来自己会过/想到的东西，还能打的很快
今天看blogs的时候看到集训队的dalao 1H打完了D1T1，当时愣住了
这个题在现在做我还打了3个小时……如果在考场上怕不是直接死了
发虚之感油然而生
然后还有前几天说到的那个polaro的情况，忘板子太吃屎了
比如说，不要因为浮躁快速的开题，快速的修改，反复的修改，然后就死了
以及前几天做UR12A的时候，一个简单的可以用树状数组维护的东西
题外话：
7-1的day8的确是一场非常好的比赛
说拿不到分，可以变成我这样凉凉
但是前两题的确难度不大
T3是思路非常好的题，寻找了合法状态的等价关系
wq考场上直接碾过去了太神了

个人觉得6-27那天的状态是最好的，尤其是做B题的时候
当时我就是在思考题目的要求能够转换成什么动态维护的东西
而且在那附近几天我刚刚提到过离线动态维护答案的思路
（不过那天C题没有把dp扩展一下推出正解挺可惜的，但是自己的确没有想出来）

那么如何获得好的考试状态呢？
我也不知道 真tm完蛋
今天先写这么多……

2018-7-5 今天的总结

NOI2016

D1T2
和我一开始想象的基本相似
但是我不是很敢打，因为我不确定是否真的可以这样判断，很多地方不知道怎么实现
然后…………然后发现正解和我想的一样，so……看看题解就知道怎么实现了
可是建图的解决方法我并没有自己想出来
如果考场遇到这样的题目怎么办？
不能放弃希望，不要出现消极的态度，尽可能找到解决的办法

D2T1
我一开始一直在想的是枚举下标，维护当前的集合然后对这个集合搞事情
但是这样没有办法很快的查询/动态维护
然后我就开始想奇怪的统计方法
比如说，差分之后等于“长度为m-1的最大权连续子段”

而在发现正解把权值排序之后很快想到了做法

思考过程中我想过正解这种维护线段树的做法，但当时我在想用主席树差分然后判断
发现max没有办法差分，然后就放弃了这个思路

思路被局限了
先入为主太可怕了，如果一开始走了弯路之后很难跳出来
不仅仅是在oi中，以后的生活中也要去锻炼思维摆脱定势的能力

D2T2
感觉自己做的好鬼啊
感性理解了很多东西，编了一个算法，得到了91分
不知道noi现场能不能成功说服自己接受这么多没法证明的东西
后来看题解的时候发现我感性理解的这些东西都是有证明的
然后试着搞了一下证明发现挺对的
感性理解不一定对，但是也许帮助扩展思路啊……
总共用2h拿到了91分

D2T3
下午来了再做，看看自己2h能拿到多少分
13:50---16:09拿到了71分
感觉4号数据是很关键的……恩……
觉得这个题实际上是计算思维的一个体现吧，十分需要思考
如果大脑没有进入这个题的模式，没有想进去的话十分难拿分
如何用有限的条件实现复杂的功能，可能这就是造计算机吧……

所以在机房的条件下，我可以在noi2016day2拿到60+91+71
day1的话，如果是现在的我应该是85~95 + ??? + 84
……感觉挺像自己发挥正常时候的水平，菜菜的，并不突出
但是国赛能不能像在机房一样发挥就不得而知了

其实noi2016我一开始，相较2017来说看上去是完全没有思路
但是推着推着，包括之前听过一点解题的思路，然后自己就怼出来了很多分数
但是一开始我是真的虚的，感觉这个题目什么都不会做
但是在考场上的话……我觉得应该没有这么冷静的去分析T3,
T2也不一定能冷静的理解我上午yy的那些性质
T1的话我还是觉得自己特别蠢，
思路稍微换一下就出来了，就是要卡在一个局限的小思路里面想
能拿分的算法不一定能优化到更高的分数，
还<del>需要更多的高能瓦斯<del>得让思路更广一些，多想想其他的做法

近两年的noiYY完了，接下来完整的时间做一下16年的unr，
小块的时间就继续补最近ur的题目
ur做完11之后去做一下pkuwc&pkusc的题目，
然后最后练习搜索类型的提答，以及各种课件之类的

UR12B
自己想了和之前几道竞赛图题目类似的解法
这样能获得的分数是49分暴力，是m=0的特判加上2^n×n的暴力
然后感觉正解的思路非常巧妙

我们可以考虑期望的线性性，那么每一个完全由S--->U-S的联边方式都会对ans贡献1
然后我们知道，当S集合大小相同的时候（假设为x），
如果没有非5000边，形成这样的边集概率应该是相同的，即0.5^(n-x)*x
那么如果出现了非5000边，设其概率为p，我们把原来的概率乘上2p即可
我觉得这个2p非常的妙啊，这样我们的问题就变成了统计某个大小的点集对于的所有2p的和，
然后最后枚举S集合大小，用个组合数啥的选一下点，最后再统一乘上对应0.5的次方就行了
这样一个比较显然的思路就是枚举在S--->U-S边集中的非5000边，
复杂度是2^m * n^2 就可以拿到更高的分数
而正解的话，我们可以直接枚举某个非5000边联通块中在S集合中的点数，
这样还是可以算贡献的，但是复杂度就少了一个n，就能过了

这个期望线性性的转换是非常妙的，转换了统计的对象，使得问题变得简单

2018-7-8

什么是dp优化？
dp优化个人觉得分为2大类
数据结构优化（然后变成了毒瘤数据结构题）
或者决策优化
单调性的话，就是“当一个点不优的时候，它就永远都不会再优”
最经典的就是用单调队列存决策点了

当然这里也会有斜率优化的单调优化，
一般是找一个斜率去卡凸包，
这个如果查询斜率是单调的就可以O(n)，使用栈或者队列;否则就得带log二分了

同时斜率优化有2种实现的方式
我们可以把转移的式子化为y=kx+b的形式，
然后这个时候我们让k与i有关，x&y和j有关，
而b是我们要最大化的东西，转化为求某个斜率的直线与凸包切点
让我突然意识到这个的是ur13B，这个转换特别的妙
无法用语言描述的觉得它很妙啊

或者我们考虑决策点之间的关系，推一下什么时候决策点会变劣，
然后维护一个决策点的式子，用斜率弹栈，这个应该是nlogn单调栈的特殊情况

nlogn用栈中第二个去弹栈顶的单调栈，
这个需要二分变差时间来弹栈，保证栈中的元素变差时间也是单调的
挺厉害的，不过这样需要决策单调性来支持

然后还有一些奇怪的优化
比如针对凸性DP的wqs二分，我们给元素加上一个“附加值”，
从而控制元素的个数，得到“恰好k个元素”时候的答案

2018-7-11

关于容斥&期望&计数
什么是期望？
期望=sigma（事件i发生概率×权值）
期望步数（事件x）=积分（第i步仍未达到事件x）
如果概率是可以容斥的，那么期望就是可以容斥的
以及有minmax容斥
容斥真tm巧妙
容斥并不一定要在指数级复杂度的题目中才能应用
我们也可以对于数据范围更大的题目使用容斥
如果需要容斥的东西只和数量有关，而不会因为具体选谁带来更多的影响
也就是说可以直接计数/乘组合数的情况
比如说有一种DP是维护“至少偶数个不合法的答案-至少奇数个不合法答案”
这样最后得到的就是没有不合法元素的答案
clj老师的课件 看一次觉得自己重新学了一次 怎么就是记不住2333
关于期望线性性之类的东西
积分是常用的处理方法
还有什么“考虑每条边的贡献，考虑每个xxxx的贡献……”

发现自己做提答的一个问题
节奏太慢了 过于慢
不管是观察性质的速度，还是实现暴力小程序的速度
而且会做很多无用功，手速也不够快
这个缺点应该没有办法提高太多了
那么如果真的有提答的话，只能是提醒自己紧张起来提升状态了
上次做thusc2016的星露谷物语的时候就有这种感觉
…………没办法
在走之前把退火敲一下，把文件操作敲一下
大概就用lnr的春游吧
这个等下次自由做题再搞

图论题……？
如果给了一个普通的图，提取关键的元素往往是解题关键
比如……要求边权最小blabla可以考虑MST啊，点双之类的可以考虑圆方树
然后提取图的（xxx）生成树是一种解题思路

“使得两个集合最大值之和最小”
可以单调枚举其中一个集合再搞另外一个集合？

2018-7-12

今天考的题是福建的集训题
md被吊打了
T1是一个比较有意思的网络流，正解里面对Ai和时间的同时限制是非常巧妙的
我们有一个“第i个人同一时刻不能持有超过ai个元素”的限制，
每个时刻有一个点对可以进行一次运送，要最大化运送到1的元素个数
那么此题的处理方法是在把时间分层那个限制从inf变成ai
意思就是“不能将超过ai种物品从这个时刻保留到下一个时刻”

T2的考场代码有一个细节没有注意到，是对于min_25筛的一个变种
我们是绝对不能枚举1的个数的：反正贡献的是2的次幂，直接预处理个数然后初始化就行了
由于枚举了1,我的复杂度从n+K退化到了最坏n*sqrt(K)
这个细节问题是我没有注意到的
而且正解我现在也没有想明白该怎么做……

T3的提答是给了10道水题，然后随机数据，开大数据范围到1e9让你跑
觉得这个挺奇妙的，主要有一点是利用数据随机不会出现太多重复数字然后开一个char表示来卡内存
这个的确没有想到

然后晚上考了unr的bishi……发现bishi的确不太难啊
明天要考unr的day1了……加油吧

 2018-7-13

今天进行了UNR1的测试！
有8位dalaoAK！
hz最高分是wzz200/250！
我得到了115分的……

现在回顾一下其实……
T1：”冷静分析一下就知道它没有决策单调性啊“
然后我一开始发现22没有决策单调性，然后……
就不肯放弃这个决策单调性的想法，一直对着它干
中间打错还调了半天，最后什么都没有
而正解是对堆的暴力进行优化

T2：“对于大部分OIER来说的大力猜结论题”
？？？猜结论？？？
打看这个题开始我就没有去想贪心啊
至少1页半的人A掉了啊……
没有搞结论题/性质题的能力
遇到这种题找不出来，也基本不会去猜结论
现在只会猜决策单调性

T3是非常清真的一个小数据结构题
考试的时候想到了一个不太正常的思路，然后顺着想下去了，
然后就变成了”维护线段树前缀和的区间异或“，然后
傻逼的是我停不下来
这个傻逼的思路我就顺着它想下去了，丝毫没有转弯去想其他思路的想法或者说意识
所以这样我的成绩就很大程度受限于一眼看上去思路对不对咯……

对于两两不同的集合，通过枚举二进制每一位，相同的分到一起，然后处理两集合之间的点对
这样可以枚举到所有的点对，因为一定两个元素是存在某一位不一样的
如果能处理集合间点对的信息和处理单个点对的时间一样，我们复杂度就快了，直接n^2变nlogv

拆出入点之后流量限制可以限制出度和入度

2018-7-15

嘛……明天就要走啦。国赛，国赛！