康托的对角论证法

对角论证法是乔治·康托尔提出的用于说明实数集合是不可数集的证明。

对角线法并非康托关于实数不可数的第一个证明，而是发表在他第一个证明的三年后。他的第一个证明既未用到十进制展开也未用到任何其它数字系统。自从该技巧第一次使用以来，在很大范围内的证明中都用到了类似的证明构造方法。

实数

康托的原始证明表明区间[0，1]中的点数不是可数无穷大。该证明是用反证法完成的，步骤如下：

  1. 假设(从原题中得出)区间[0，1]中的点数是可数无穷大的
  2. 于是乎我们可以把所有在这区间内的数字排成数列, (r_1, r_2, r_3, ... )
  3. 已知每一个这类的数字都能以小数形式表达
  4. 我们把这些数字排成数列(这些数字不需按序排列; 事实上，有些可数集, 例如有理数也不能按照数字的大小把他们全数排序，但单只是成数列就没有问题的)在部份有多种表达形式的数字上，例如0.499 ... = 0.500 ..., 我们选择前者.
  5. 举例，如果该数列小数形式表现如下:
    r1 = 0 . 5 1 0 5 1 1 0 ...
    r2 = 0 . 4 1 3 2 0 4 3 ...
    r3 = 0 . 8 2 4 5 0 2 6 ...
    r4 = 0 . 2 3 3 0 1 2 6 ...
    r5 = 0 . 4 1 0 7 2 4 6 ...
    r6 = 0 . 9 9 3 7 8 3 8 ...
    r7 = 0 . 0 1 0 5 1 3 5 ...
    ...
  6. 考虑r_k小数点后的第k个位，为了方便起见, 我们底间并粗体这些数字，从下图你应明白为什么这个证明被称为对角论证法
    r1 = 0 . 5 1 0 5 1 1 0 ...
    r2 = 0 . 4 1 3 2 0 4 3 ...
    r3 = 0 . 8 2 4 5 0 2 6 ...
    r4 = 0 . 2 3 3 0 1 2 6 ...
    r5 = 0 . 4 1 0 7 2 4 6 ...
    r6 = 0 . 9 9 3 7 8 3 8 ...
    r7 = 0 . 0 1 0 5 1 3 5 ...
    ...
  7. 我们设一实数x \in [0,1], 其中x是因应以下的方式定义的
    • 如果r_k的第k个小数位等于5, 那么x的第k个小数位是4
    • 如果r_k的第k个小数位不等于5, 那么x的第k个小数位是5
  8. 明显地x是一个在区间[0，1]内的实数，以之前的数为例, 则相对应的x应为 0 . 4 5 5 5 5 5 4 ...
  9. 由于我们假设(r_1,r_2,r_3,... )包括了所有区间[0, 1]内的实数，所以一定有一个r_n=x
  10. 但由于x的特殊的定义，这使到x和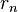r_n的第n个小数位是不同的，所以x \notin (r_1,r_2,r_3,... )
  11. 所以(r_1,r_2,r_3,... )并不能罗列所有区间[0, 1]内的实数，这发生了矛盾。
  12. 所以在第一点内所提出的假设"区间[0，1]中的点数是可数无穷大的"是不成立的。

 

视频讲解

http://v.youku.com/v_show/id_XMTYyMzg2NDc2.html

posted @ 2012-09-12 22:33  LYLtim  阅读(2119)  评论(0)  编辑  收藏  举报