语音主观和客观评价总结与实现

语音信号处理一般都要进行主观评价实验和客观评价实验。

  • 主观评价：邀请测听者对语音进行测听，测听者根据语音的质量和可理解性 给出主观意见得分
  • 客观评价：根据算法来衡量语音质量

　　主观听力测试可能是评估语音质量或语音清晰度最可靠的方法。但是主观评价实验受到以下限制：

  • 需要训练有素的听众
  • 需要消耗更多的时间成本和人力成本
  • 测听者受多种因素影响，容易影响到主观评价结果，如个体受试者的偏好和实验的环境(其他条件)。

　　出于以上原因，研究人员设计了一些客观评价来评估语音质量。理想的客观评价方法应该能准确地预测由正常听力者进行的主观听力测试的结果，应包括语音不同处理层次的信息，包括低级信息(如心理声学)和高级信息(如语义、语言学和语用学)。本文概述了多种客观评价方法，这些方法已被用来评估质量和可理解度的语音处理的降噪算法。

本章需要使用的python库：

  • pesq库： pip install pypesq 
  • pysepm库：pip install https://github.com/schmiph2/pysepm/archive/master.zip 
  • pystoi 库： pip install pystoi 

主观评价

　　主观语音质量测量可以通过主观听力测试获得，在主观听力测试中，参与者根据意见量表对系统的性能或信号质量进行评价[表1]。主观听力测试通常由几个受试者进行，他们将听原始的(如果有的话)，通过增强算法退化和增强的语音信号。受试者使用预定义的听力质量量表提供他们对每个信号质量的意见。最后，通过平均分得到的MOS值表明了被测算法的主观质量。为了获得一个真实的MOS，需要大量的受试者。因此，主观质量测量的主要缺点是成本。即使有大量的被试，MOS的方差也可能很高。此外，从测试中获得的主观评分还取决于听力工具的类型和质量(耳机或扬声器)和环境条件。

　　主观质量评价可分为相对偏好法和绝对品类评价法两类。在相对偏好方法中，听者被提供成对的语音刺激。它们是参考刺激和测试刺激。听众在听经过处理的演讲之前，将未处理的演讲作为参考呈现给他们。在绝对类别评价方法中，只提出了试验刺激。

　　这一般分为两个阶段，即训练和评估阶段。在训练阶段，向听众提供一组参考信号及其评级。

相对偏好的方法

绝对类别评级方法

主观方法就是通过人类对语音进行打分，比如MOS、CMOS和ABX Test。

如何评估语音质量好坏？

绝对等级评价(ACR)

失真等级评价(DCR)

相对等级评价(CCR)

MOS

　　最常用和相对简单的主观质量指标是分级判断方法，采取５个级别对被测语音的质量进行评价。待测语音的质量是在所有试听人员的评分上求平均得到的。这种方式被称作平均意见得分（Mean Opinion Score, MOS）。下表给出了语音评价的等级分级。

评分 语音质量 失真程度
5 非常好（Excellent） 不可察觉（Imperceptible）
4 好（Good） 略可察觉（Not annoying）
3 一般（Fair） 可察觉（Slightly annoying）
2 差（Poor） 不可接受（Not objectionable）
1 很差（Bad） 难以接受（objectionable）

MOS评分有两个阶段。训练阶段，听者需要听一系列参考信号，保证大家对质量评级的标准尽可能一致；评估阶段，试听人员对所听到的信号，进行主观打分。

客观评价

　　客观评价的度量可以分为有参考度量和无参考度量。

  • 有参考 (基于输入-输出)：将 经过语音系统的 输出语音 和 参考语音 进行比较，得到客观打分
  • 无参考 (基于输入)：仅根据 输出语音 进行打分

一般来说，客观的语音质量指标可以分为

  1. 基于信噪比(SNR)的评价方法
  2. 频谱距离的评价方法
  3. 基于 线性预测系数(LPCs)的 评价方法
  4. 基于听觉感知的距离度量方法

基于SNR的语音质量评价

信噪比(SNR)

定义：纯净语音$s(n)$功率$P_{signal}$与噪声$d(n)$功率$P_{noise}$的比（此处功率为平均功率）

$$SNR(dB)=10\log_{10}\frac{\sum_{n=0}^{N-1}s^2(n)}{\sum_{n=0}^{N-1}d^2(n)}=10*\log_{10}(\frac{P_{signal}}{P_{noise}})$$

$$SNR(dB)=10\log_{10}\frac{\sum_{n=0}^{N-1}s^2(n)}{\sum_{n=0}^{N-1}[x(n)-s(n)]^2}$$

缺点：

  1. 一好遮百丑：SNR计算的是整个信号的全局平均值。如果一段音频中，只有一小段非常响亮且干净的部分，它会极大地拉高整体的SNR值，即使其他安静部分的噪声很严重。
  2. 忽略人耳听觉特性：人耳对不同频率的声音敏感度不同（例如，对1-4kHz的中频最敏感，对低频和超高频不敏感）。全局SNR平等地对待所有频率的噪声，这与主观听感有很大出入。
def get_snr(speech, noise):
    assert speech.ndim == noise.ndim, "speech和noise的维度不一样"

    power_speech = np.mean(speech**2)
    power_noise = max(np.mean(noise**2), 1e-10)

    snr = 10 * np.log10(power_speech / power_noise)
    return snr

分段信噪比(SegSNR)

为了解决SNR的第一个问题（“一好遮百丑”），分段信噪比 (Segmental SNR, SNRseg) 被提了出来。

核心思想：不再计算整个信号的SNR，而是将信号切分成很多短的帧 (Frame)（例如每帧20-30毫秒），单独计算每一帧的SNR，最后再将所有帧的SNR值（通常是dB值）取平均。

$$SNRseg=\frac{10}{M} \sum_{m=0}^{M-1} \log _{10} \frac{\sum_{n=N m}^{N m+N-1} x^{2}(n)}{\sum_{n=N m}^{N m+N-1}[x(n)-\hat{x}(n)]^{2}}$$

其中

  • $x(n)$：原始(干净)信号
  • $\hat{x}(n)$：增强信号
  • $N$：帧长
  • $M$：信号中的帧数量

缺点：

  1. SNRseg有一个潜在问题，语音信号(在会话语音中非常丰富)在安静期间的信号能量非常小，导致较大的负SNRseg值，这将使整体评估出现偏差。为了解决这一问题使用VAD只计算有语音段的SNR。
  2. 忽略了人耳对不同频率的敏感度差异。在SNRseg的计算中，一帧内的低频噪声和中频噪声被同等看待。

　　后续研究通过将 log 函数移动 1 提出了分段 SNR 的不同定义，即

$$\mathrm{SNR} \operatorname{seg}_{\mathrm{R}}=\frac{10}{M} \sum_{m=0}^{M-1} \log _{10}\left(1+\frac{\sum_{n=N m}^{N m+N-1} x^{2}(n)}{\sum_{n=N m}^{N m+N-1}(x(n)-\hat{x}(n))^{2}}\right)$$

　　这样做可以避免在沉默(silent)语音帧期间获得大的负值的可能性。 因为SNRseg_R的最小可值现在为零而不是负无穷大。 上述分段 SNR 定义的主要优点是它避免了对语音和无语音帧进行显式标记的需要。 

python代码

import pysepm

pysepm.SNRseg(clean_speech, noisy_speech, fs)

具体细节

def SegSNR(clean, noisy, frame_length: int, hop_length: int):
    assert clean.shape == noisy.shape, "clean和noisy的维度不一样"

    # 分帧
    clean_frames = librosa.util.frame(clean, frame_length=frame_length, hop_length=hop_length)  # (frame_length, n_frames)
    noisy_frames = librosa.util.frame(noisy, frame_length=frame_length, hop_length=hop_length)  # (frame_length, n_frames)

    # 计算每帧的信噪比
    snr_frames = []
    for i in range(clean_frames.shape[1]):
        clean_frame = clean_frames[:, i]
        noisy_frame = noisy_frames[:, i]
        # 跳过静音帧
        if np.all(np.abs(clean_frame) < 1e-6) or np.all(np.abs(noisy_frame) < 1e-6):
            continue
        snr_frames.append(get_snr(clean_frame, noisy_frame))

    # 如果所有帧都是静音
    if not snr_frames:
        return float('-inf')

    return np.mean(snr_frames)

频率加权分段信噪比（fwSNRseg）

【论文】2009_Objective measures for predicting speech intelligibility in noisy conditions based on new bandimportance functions

　　频率加权分段信噪比（Frequency-weighted Segmental SNR，fwSNRseg）在计算每一帧的信噪比之前，先对信号和噪声的频谱进行频率加权。这个权重模仿了人耳的听觉特性，即对敏感的频率区域（如中频）赋予更高的权重，对不敏感的频率区域（如低频和高频）赋予较低的权重。

FWSSNR可定义为：

$$\text { fwSNRseg }=\frac{10}{M} \sum_{m=0}^{M-1} \frac{\sum_{j=1}^{K} W_{j} \log _{10}\left[X^{2}(j, m) /(X(j, m)-\hat{X}(j, m))^{2}\right]}{\sum_{j=1}^{K} W_{j}}$$

其中

  • $W_j$：第$j$个频带的权重
  • $K$：频带的数量
  • $M$：信号的帧数
  • $X(j,m)$：纯净信号在第$j$个频带第$m$帧处的滤波器组 幅值(amplitude) （第m帧第j个频带经过高斯形窗加权的干净信号频谱）
  • $\hat{X}(j,m)$：同一频带增强信号的滤波器组 幅值(amplitude)
import pysepm

fwSNRseg = pysepm.fwSNRseg(clean_speech, enhanced_speech, fs)

权重可以通过回归分析得到(有兴趣的可以搜索frequency-variant objective measures)，另一种方法就是查表，如下表所示。

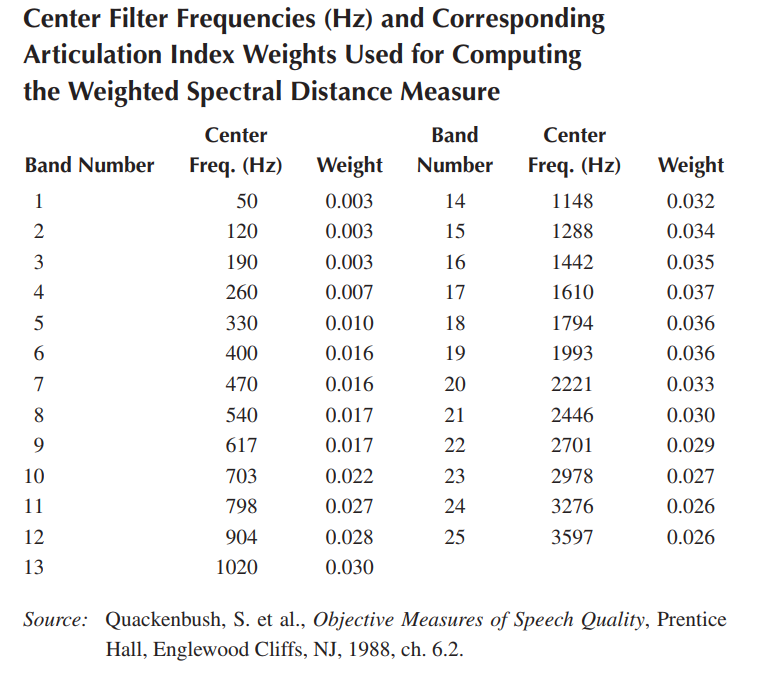
峰值信噪比(PSNR)

　　表示信号的最大瞬时功率和噪声功率的比值，最大瞬时功率为语音数据中最大值得平方。

$$SNR(dB)=10\log_{10}\frac{MAX[s(n)]^2}{\frac{1}{N}\sum_{n=0}^{N-1}[x(n)-s(n)]^2}=20\log_{10}\frac{MAX[s(n)]}{\sqrt{MSE}}$$

其中，$s(n)$是干净语音、$x(n)$是带噪语音。

缺点：PSNR基于纯数学的均方误差，它无法很好地模拟人类的听觉感知。人耳对不同频率的噪声敏感度不同，并且存在掩蔽效应（一个强的声音会掩盖掉一个弱的声音）。PSNR无法体现这些复杂的听觉心理学现象。两个信号可能有相似的PSNR值，但听起来质量差异巨大。

def PSNR(clean, noisy, max_val=None):
    assert clean.shape == noisy.shape, "clean和noisy的维度不一样"

    # 如果没有指定最大值，使用clean信号的实际最大值
    if max_val is None:
        max_val = np.abs(clean).max()

    # 计算均方误差 (MSE)
    mse = np.mean((clean - noisy) ** 2)

    # 避免除以0
    if mse == 0:
        return float('inf')

    # 计算PSNR
    psnr = 10 * np.log10(max_val**2 / mse)
    return psnr

但需要注意在做不同算法对比时，max_val 应该保持一致（通常使用原始干净音频的峰值）。

尺度不变的信号失真比(SI-SDR)

【论文】2019_SDR–half-baked or well done?

　　Scale-invariant signal to distortion ratio (SI-SDR)是一种用于衡量估计信号（Estimated Signal）与参考信号（Reference Signal）之间保真度的客观度量标准。它主要应用于语音分离 (Speech Separation) 和 语音增强 (Speech Enhancement) 等任务中。

它的全称揭示了其核心特点：

  • SDR：信号与失真（或噪声）的比率，这是衡量信号质量的经典概念。比率越高，说明有用信号的能量远大于失真/噪声的能量，质量越好。
  • SI：尺度不变。这是SI-SDR与传统SDR最关键的区别。它意味着评估结果不会因为估计信号的整体音量（幅度）发生变化而改变。

简单来说，SI-SDR衡量的是模型输出的语音在“波形上”与原始纯净语音有多像，而不关心它的音量是大了还是小了。

$$\begin{aligned}
\text { SI-SDR } &=10 \log _{10}\left(\frac{\left\|e_{\text {target }}\right\|^{2}}{\left\|e_{\text {res }}\right\|^{2}}\right)=10 \log _{10}\left(\frac{\left\|\frac{\hat{s}^{T} s}{\|s\|^{2}} s\right\|^{2}}{\left\|\frac{\hat{s}^{T} s}{\|s\|^{2}} s-\hat{s}\right\|^{2}}\right)
\end{aligned}$$

def si_sdr(reference, estimate, epsilon=1e-8):
    """
    计算尺度不变信噪比 (Scale-Invariant Signal-to-Distortion Ratio, SI-SDR)。

    Args:
        reference (np.ndarray): 原始的、干净的参考信号 (一维数组)。
        estimate (np.ndarray): 模型估计或处理后的信号 (一维数组)。
        epsilon (float): 一个非常小的数值，用于防止分母为零，保证数值稳定性。

    Returns:
        float: SI-SDR 值，单位为分贝 (dB)。
    """
    assert reference.shape == estimate.shape, "reference和estimate的维度不一样"

    # 2. 零均值化 (可选但推荐)
    # 移除直流分量，使计算更关注信号的动态变化
    reference = reference - np.mean(reference)
    estimate = estimate - np.mean(estimate)

    # 3. 计算目标信号分量 (s_target)
    # s_target 是 estimate 在 reference 上的投影
    # 公式: s_target = (<ŝ, s> / ||s||²) * s
    dot_product = np.dot(estimate, reference)   # <ŝ, s> (点积)
    norm_s_squared = np.dot(reference, reference)   # ||s||² (s的能量)
    
    # 检查参考信号能量，避免除以零
    if norm_s_squared < epsilon:
        # 如果参考信号几乎是静音，SI-SDR没有意义
        return -np.inf # 返回负无穷或np.nan

    alpha = dot_product / (norm_s_squared + epsilon)    # 最佳缩放因子 α
    s_target = alpha * reference
    
    # 4. 计算误差/失真分量 (e_noise)
    e_noise = estimate - s_target
    
    # 5. 计算 SI-SDR
    # SI-SDR = 10 * log10 ( ||s_target||² / ||e_noise||² )
    power_s_target = np.sum(s_target**2)    # ||s_target||²
    power_e_noise = np.sum(e_noise**2)      # ||e_noise||²
    
    # 同样加上 epsilon 防止除以零
    if power_e_noise < epsilon:
        # 如果噪声能量极小，说明匹配得非常好
        return np.inf # 返回正无穷

    si_sdr_val = 10 * np.log10(power_s_target / (power_e_noise + epsilon))
    
    return si_sdr_val

 

基于LPC系数的客观评价

　　LPC（Linear Predictive Coding）是一种用线性预测模型表示语音信号频谱的方法。它假设当前语音采样点可以由前 p 个采样点的加权和来预测：

$$\hat{s}(n) = \sum_{k=1}^{p} a_k \cdot s(n-k)$$

其中：

  • $a_k$是 LPC 系数 （prediction coefficients）
  • p 为预测阶数（通常 10~16 阶即可较好描述人声）
  • $e(n)=s(n)−s^(n)$ 预测误差（残差信号）

在频域上，LPC 系数可以拟合语音短时谱的包络（spectral envelope），能有效反映共振峰（formants）位置和形状。因此，如果两个语音的 LPC 系数差异很小，则它们的共振峰结构也相近，感知上音质差别小。

优点：

  • 实现简单，计算速度快
  • 对语音共振峰特征敏感，比较契合听觉上的音色判断
  • 可应用于不同的编码码率、降噪算法、合成方法的对比

缺点：

  • 对时序失配敏感，需要先做语音对齐（Time Alignment）
  • 无法直接反映主观感受（忽略了韵律、瞬态等听感因素）
  • 依赖于分帧参数（帧长、阶数、加窗函数等）的设定

将 LPC 系数转化为可比空间

　　直接比较 ( a_k ) 并不好，因为它们不稳定且不具有感知相关的等距性。 常见做法是将 LPC 系数转化为 反射系数（Reflection Coefficients, RC） 或 线谱对（Line Spectral Pairs, LSP），其中 LSP 特别适合做失真度量，因为在频域上有良好的单调性和稳定性。

转化过程（以 LSP 为例）：

  1. 求出 LPC 系数 $a_k$
  2. 将其转换为 LSP 参数 $\omega_i$ (单位：rad/sample)
  3. 对比两个语音对应帧的 LSP 参数差值

失真度量方法

假设参考语音（Reference）和测试语音（Test）在第 m 帧的 LSP 参数分别为：

$$\{\omega_{1}^{(R)}, \omega_{2}^{(R)}, \dots, \omega_{p}^{(R)}\}$$

常用的失真度量方式有：

均方差 (MSE)

$$d_m = \frac{1}{p} \sum_{i=1}^{p} \left( \omega_i^{(R)} - \omega_i^{(T)} \right)^2$$

频率加权均方差

考虑低频对感知的更大影响，可加权：

$$d_m = \frac{1}{p} \sum_{i=1}^{p} w_i \cdot \left( \omega_i^{(R)} - \omega_i^{(T)} \right)^2$$

其中$w_i$可按 Bark 或 Mel 频率尺度设计。

谱失真 (Spectral Distortion, SD)

直接通过 LPC 系数形成功率谱包络 P(\omega) ，再比较能量差：

$$SD = \sqrt{ \frac{1}{2\pi} \int_{-\pi}^{\pi} [10 \log_{10} P_R(\omega) - 10 \log_{10} P_T(\omega) ]^2 d\omega }$$

在工程上积分用 FFT 近似。

工程实现建议

  1. 预处理：去直流分量，预加重 (Pre-emphasis)
  2. 分帧 + 加窗：25ms 帧长，10ms 帧移，汉明窗
  3. LPC 计算：阶数 10~16，根据采样率选择
  4. LPC → LSP 转换，提高稳定性
  5. 失真度计算：MSE + 可选加权
  6. 全段统计：均值、方差，绘出失真随时间的变化曲线

mermaid_chart

基于频谱距离的客观评价

　　基于频谱距离（Spectral Distance）的客观评价方法，是通过比较测试语音与参考语音在频域上的差异来量化音质好坏的指标。谱距离适用于语音编码、语音增强、语音合成等场景。常用指标公式 有频谱距离（Spectral Distance, SD）、对数频谱距离（Log Spectral Distance, LSD）、倒谱距离（Cepstral Distance）。

常用语音超分、语音编码、语音增强等场景。

频谱距离(SD)

$$SD = \frac{1}{M}\sum_{m=1}^{M} \sqrt{\frac{1}{K} \sum_{k=1}^{K} \left(20 \log_{10} \frac{|X_m(k)|}{|Y_m(k)|} \right)^2}$$

其中：

  • $M$：帧数
  • $K$：每帧FFT点数（谱线数）
  • $X_m(k)$、$Y_m(k)$：第 m 帧参考语音与测试语音在 k 频点的幅度值

对数谱距离(LSD)

　　对数刻度更符合人耳对音强变化的感知：

$$LSD =  \sqrt{\frac{1}{T} \sum_{t=1}^{T} \frac{1}{F} \sum_{f=1}^{F} \left(10 \log _{10}|S(t,f)|^{2}-10 \log _{10}|\hat{S}(t,f)|^{2} \right)^2} $$

　　式中，$f$和$t$分别为频率索引和帧索引，$T$为语音帧数，$F$为频点数，$\hat{S}(t,f)$和$S(t,f)$分别为估计音频和宽带音频经过短时短时傅里叶变换后的幅度谱。

def lsd(reference, estimate, n_fft=2048, hop_length=512, win_length=None):
    assert reference.ndim == 1 and estimate.ndim == 1, "输入信号必须是一维数组。"
    
    if win_length is None:
        win_length = n_fft

    reference_stft = librosa.stft(reference, n_fft=n_fft, hop_length=hop_length, win_length=win_length) # (F,T)
    estimate_stft = librosa.stft(estimate, n_fft=n_fft, hop_length=hop_length, win_length=win_length) # (F,T)

    reference_power_spec = np.abs(reference_stft) ** 2 # (F,T)
    estimate_power_spec = np.abs(estimate_stft) ** 2 # (F,T)

    reference_log_power_spec = 10 * np.log10(reference_power_spec + EPS)
    estimate_log_power_spec = 10 * np.log10(estimate_power_spec + EPS)

    squared_error = (reference_log_power_spec - estimate_log_power_spec) ** 2
    lsd_val = np.sqrt(np.mean(squared_error))

    return lsd_val

梅尔倒谱距离 (MCD)

【论文】Mel-cepstral distance measure for objective speech quality assessment

　　倒谱（Cepstrum）是由log 频谱经过一次反傅里叶变换（或 DCT）得到的序列。倒谱系数（Cepstral coefficients）正是用来捕捉声道包络特征的，因此比较两个语音的倒谱系数差异，就等于比较它们的频谱包络差异。类比：频谱比较的是“曲线高度”，倒谱比较的是这条曲线“形状”的差异。

它的物理意义是：

  • 高频部分反映激励信号（如声带振动周期）信息
  • 低频部分反映声道频率响应（共振峰）信息

梅尔倒谱距离(Mel-cepstral distance, MCD)是 Kubichek 提出的改进版，把频谱先映射到 Mel 频率刻度后再取倒谱，更符合人耳分辨率特性

$$CD = \frac{10}{\ln 10} \sqrt{ 2 \sum_{n=1}^{P} [c_n - \hat{c}_n]^2 }$$

其中：$P$ 是倒谱系数的个数（常用 12 或 24），梅尔倒谱系数 $ c_n $、$\hat{c}_n $ 

基于听觉感知的客观评价

　　该类评价方法是以人感知语音信号的心理听觉特性为基础。具有代表性的听觉模型方法有BSD、MBSD、PSQM、PESQ、PLP、MSD(Mel Spectral Distortion)等。

加权斜率谱距离(WSS)

WSS 是 Klatt（1982）提出的一种基于听觉模型的频谱形状差异测度。它认为：

  • 人耳对共振峰（Formant）附近的谱形变化更敏感
  • 谱倾斜（slope）变化比绝对幅度干扰更重要

因此，WSS 通过**临界带滤波 + 对数能量差分 → 峰值感知加权**来量化两个语音信号的谱形差异，WSS 值越小，说明失真越少。

1、临界带滤波

  • 常用 Bark 尺度（约 36 个频带）
  • 对信号经每个临界带滤波器求对数能量：$C_x(k),\ \bar{C}_x(k)$

其中 k 为频带索引，C_x(k) 对应参考信号，\bar{C}_x(k) 对应测试/增强信号

3、加权系数计算

　　对每个频带，根据全局峰值与最近局部峰值位置计算权重：

$$W(k) = \frac{K_{\max}}{K_{\max} + C_{\max} - C_x(k)} \cdot \frac{K_{\text{locmax}}}{K_{\text{locmax}} + C_{\text{locmax}} - C_x(k)}$$

  • $K_{\max}$：全局最大峰的频带索引
  • $C_{\max}$：全局最大峰幅度
  • $K_{\text{locmax}}$：距离当前频带最近的局部峰索引
  • $C_{\text{locmax}}$：最近局部峰的幅度

加权系数使得接近峰值区域的谱差异影响更大

4、帧内 WSS 计算

$$d_{\text{WSSM}}(m) = \frac{\sum_{k=1}^{K} W(k) \cdot [S_x(k) - \bar{S}_x(k)]^2} {\sum_{k=1}^{K} W(k)} $$

其中 m 为帧编号，K 为临界带数（一般 36）

5、全局 WSS

$$WSS_{\text{total}} = \frac{1}{M} \sum_{m=1}^{M} d_{\text{WSSM}}(m)$$

  • M：总帧数

优点：

  • 与人耳对共振峰偏移的感知高度相关
  • 对幅度标度变化不敏感，专注于谱形变化

缺点：

  • 对背景噪声敏感（噪声会扰动频带能量差，导致权重变化）
  • 计算相对复杂，比 LSD/SD 慢
import pysepm

pysepm.wss(clean_speech, enhanced_speech, fs)

Bark谱失真 (BSD) 

　　巴克谱失真(Bark Spectral Distortion, BSD) 度量是基于语音质量与语音响度直接相关的假设。响度是一个心理声学术语，定义为听觉的大小。它本质上是一个包含心理声学反应的客观测量。BSD度量定义为原始语音和干扰或增强语音估计响度的平均平方欧氏距离。为了计算响度，使用心理声学测量结果对语音信号进行处理，包括：临界频带分析、等响度预加重(equal loudness pre-emphasis)和强度-响度幂律(intensity-loudness power law)。BSD测度计算为

$$B S D=\frac{1}{M} \frac{\sum_{m=1}^{M} \sum_{b=1}^{K}\left[L_{s}(b, m)-L_{d}(b, m)\right]^{2}}{\sum_{m=1}^{M} \sum_{b=1}^{K}\left[L_{s}(b, m)\right]^{2}}$$

其中K为临界频带数，$L_s(b, m)$和$L_d(b, m)$分别为原始语音和干扰语音或增强语音对应的第m帧第b个临界频带的Bark谱。BSD在浊音区域的失真代表整体失真的情况下工作良好，因为它只处理浊音区域;因此，必须检测语音区域。

import pysepm

pysepm.bsd(clean_speech, enhanced_speech, fs)

改进的Bark谱失真

　　MBSD度量将噪声掩蔽阈值的概念纳入到传统的BSD度量中，任何低于噪声掩蔽阈值的失真都不包括在BSD度量中。MBSD度量的概念框图如下图所示。传统的BSD和MBSD有两个不同之处。首先，MBSD使用噪声掩蔽阈值来确定声音失真，而BSD使用经验确定的功率阈值。其次，BSD和MBSD的失真计算是不同的。BSD将失真定义为估计响度的平均平方欧氏距离，而MBSD将失真定义为估计响度的平均差值。

　　通过临界频带分析、传播函数应用和绝对阈值的考虑，对噪声掩蔽阈值进行了估计。该噪声掩蔽阈值估计考虑了音调掩蔽噪声和噪声掩蔽音调。将噪声掩蔽阈值的响度与原语音和编码语音的响度差进行比较，以确定失真是否可感知。当响度差低于噪声掩蔽阈值时，该响度差是不可见的。

　　因此，它不包括在MBSD的计算中。因此，MBSD计算为：

$$M B S D=\frac{1}{N} \sum_{j=1}^{M}\left[\sum_{i=1}^{K} Z(i)\left|L_{s}(i, m)-L_{d}(i, m)\right|^{n}\right]$$

　　其中，$L_s(i, m)$和$L_d(i, m)$分别表示第$m$帧纯净语音和干扰/增强语音的Bark频谱。$K$是临界频带的总数，$M$是帧的总数。$Z(i)$是可感知失真的指示器。当失真可感知时，$Z(i)$为1，否则$Z(i)$为0。这是通过比较响度和噪声掩蔽阈值得到的。

语音质量感知评估 (PESQ)

引言：我先做个简要介绍，再讲使用。使用之前建议还是详细了解一下，不要用错了，导致论文被拒，或者做了伪研究，以下内容是我挑重点摘自ITU-T P862建议书，比较权威，重要的地方我会加粗。想要进一步了解的自行去下载原文。

　　语音质量感知评估 (Perceptual Evaluation of Speech Quality, PESQ)是由国际电信联盟(International Telecommunication Union，ITU) 2001年提供的ITU-T P862建议书：语音质量的感知评估（PESQ）：窄带电话网络和语音编解码器的端到端语音质量评估的客观方法，并提供了ANSI-C语言实现代码。真实系统可能包括滤波和可变延迟，以及由于信道误差和低比特率编解码器引起的失真。国际电联电信政策861中描述的PSQM方法仅被推荐用于评估语音编解码器，不能适当考虑滤波、可变延迟和短时局部失真。PESQ通过传递函数均衡、时间校准和一种新的时间平均失真算法来解决这些影响。PESQ的验证包括许多实验，这些实验专门测试了它在滤波、可变延迟、编码失真和信道误差等因素组合下的性能。

　　建议将PESQ用于3.1kHz(窄带, 8000Hz采样率)手机电话和窄带语音编解码器的语音质量评估。PESQ是属于客观评价，和主观分数之间的相关性约为0.935，但PESQ算法不能用来代替主观测试。

　　PESQ算法没有提供传输质量的综合评估。它只测量单向语音失真和噪声对语音质量的影响。响度损失、延迟、侧音、回声和其他与双向互动相关的损伤(如中央削波器)的影响不会反映在PESQ分数中。因此，有可能有很高的PESQ分数，但整体连接质量很差。

　　PESQ的感知模型用于计算原始信号$X(t)$与退化信号$Y(t)$之间的距离(PESQ分数)，退化信号$Y(t)$是$X(t)$通过通信系统的结果。PESQ的输出是对受试者在主观听力测试中给予$Y(t)$的感知质量的预测。取值在-0.5到4.5的范围内，得分越高表示语音质量越好，尽管在大多数情况下输出范围在1.0到4.5之间。

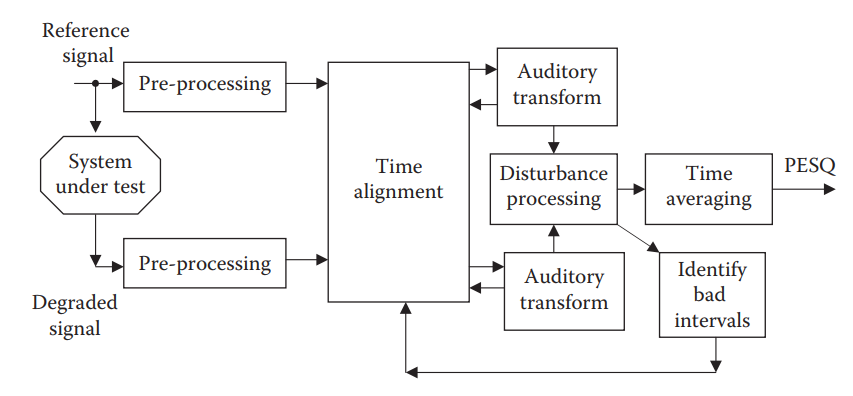
　　ITU提供了C语言代码，下载请点击这里，但是在使用之前我们需要先编译C脚本，生成可执行文件exe

编译方式为：在命令行进入下载好的文件

  1. cd \Software\source
  2. gcc -o PESQ *.c -lm

　　经过编译，会在当前文件夹生成一个pesq.exe的可执行文件

使用方式为：

  1. 命令行进入pesq.exe所在的文件夹
  2. 执行命令： pesq 采样率 "原始文件路径名" "退化文件路径名” ，采样率必须选择 +8000 (窄带 pesq)或 +16000 (宽带 pesq-wb)，
  3. 回车
  4. 等待结果即可，值越大，质量越好。
    • 例如：pesq +16000 raw.wav processed.wav

python代码实现

python实现的PESQ有两个库分别是 pesq 和 pypesq：

import pesq
import pypesq
import librosa

fs = 16000
clean = librosa.load("./p234_001_clean.wav", sr=fs)[0]
enhance = librosa.load("./p234_001_enhance.wav", sr=fs)[0]

print(pesq.pesq(fs, clean, enhance, 'wb'))  # 1.571152925491333
print(pypesq.pesq(clean, enhance, fs=fs))  # 2.643505334854126

我发现不同库算的值相差太大，另外我也跑了一下官方C语言版本的PESQ，

pesq +16000 ./p234_001_clean.wav ./p234_001_noisy.wav
...
Prediction : PESQ_MOS = 2.826

惊奇的发现没有一个库对的上官方的，但是pypesq接近，所以写论文需要用PESQ的小伙伴留个心眼啊。

PESQ 包含 3 种类型的值：NB PESQ MOS、NB MOS LQO、WB MOS LQO。此包仅返回NB PESQ MOS代表 的Raw MOS分数narrowband handset listening。

pypesq返回的是 NB PESQ MOS

pesq返回的是：WB MOS LQO，属于pesq的映射，现在用的更多的也是MOS-LQO。如果你硬是想要PESQ得分，你可以自行逆变换回去，公式见下一节

MOS-LQO

　　MOS-LQO (Mean Opinion Score – Listening Quality Objective)，使用客观测量技术评估主观听力质量)与之相对的还有MOS-LQS (Mean Opinion Score – Listening Quality Subjective) ，使用样本的主观评分直接衡量听力质量，就是主观评价了。

功能：将P.862原始结果分数转换为MOS-LQO的映射，P862.1：用于将P.862原始结果分数转换为MOS-LQO的映射函数.pdf

　　ITU-T P.862建议书 提供的原始分数在-0.5到4.5之间。希望从PESQ (P.862)得分中转换为MOS-LQO (P.862.1)分数，从而可以与MOS进行线性比较。该建议书介绍了从原始P.862得分到MOS-LQO (P.800.1)的映射函数及其性能。映射函数已在代表不同应用程序和语言的大量主观数据上进行了优化，所呈现的性能优于原始的PESQ(P862)，取值在[1, 4.5]之间，连续的。公式为：

$$公式1：y=0.999+\frac{4.999-0.999}{1+e^{-1.4945x+4.6607}}$$

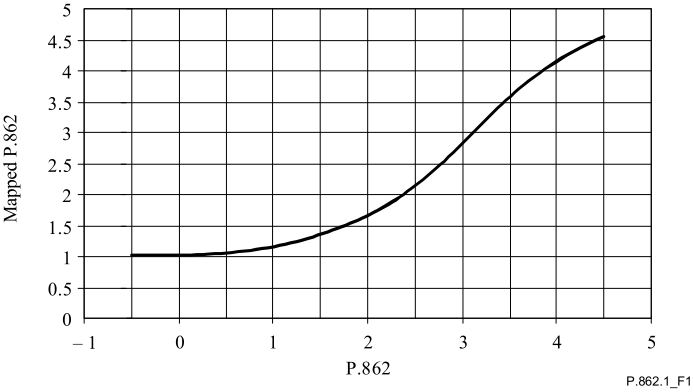
def pesq2mos(pesq):
    """ 将PESQ值[-0.5, 4.5]映射到MOS-LQO得分[1, 4.5]上，映射函数来源于：P.862.1 """
    return 0.999 + (4.999 - 0.999) / (1 + np.exp(-1.4945 * pesq + 4.6607))

公式2给出了从MOS-LQO分数到PESQ分数的转换的反映射函数

$$公式2：x=\frac{4.6607-\ln \frac{4.999-y}{y-0.999}}{1.4945}$$

def mos2pesq(mos):
    """ 将MOS-LQO得分[1, 4.5]映射到PESQ值[-0.5, 4.5]上，映射函数来源于：P.862.1"""
    inlog = (4.999 - mos) / (mos - 0.999)
    return (4.6607 - np.log(inlog)) / 1.4945

需要注意的是，所提供的函数有一些实际限制：

  • 本文提供的映射函数对源自所有类型应用程序的数据库进行了优化。仅针对特定应用程序或语言进行优化的其他映射函数可能在该特定应用程序或语言上比提供的函数执行得更好。
  • 虽然训练数据库包含分数较低的MOS区域中的样本比例很大，但是在原始P.862分数0.5到1的范围内缺少样本。在此范围内，映射的P.862函数进行插值，因此确定了预测误差Ep和平均残差Em

PESQ-WB

　　2007年11.13国际电联公布了PESQ的宽带版本(ITU-T P862.2，PESQ-WB)，P.862建议书的宽带扩展，用于评估宽带电话网络和语音编解码器，主要用于宽带音频系统 (50-7000 Hz)，16000Hz采样率，尽管它也可以应用于带宽较窄的系统。例如听众使用宽带耳机的语音编解码器。相比之下，ITU-T P.862建议书假设使用标准的IRS型窄带电话手机，在300 Hz以下和3100 Hz以上会强烈衰减。

使用范围

  1. 不建议将PESQ-WB用在信号插入点和信号捕获点之间包含噪声抑制算法的系统。 另外，应使用干净的语音样本，因为嘈杂的语音样本，即那些信噪比较差的语音样本，可能会导致预测错误。 用户还应注意，宽带语音主观实验中不同失真类别的相对排名可能会随语言种类而略有变化。 特别要注意的是，宽带扩展可能会高估ITU-T Rec.3建议书的MOS分数。
  2. 当使用PESQ-WB来比较可能对音频信号进行频带限制的系统的性能时，建议使用一个宽带（50-7000 Hz音频带宽）版本的信号作为所有参考信号。被限制带宽的测试系统会导致语音性能下降，降低输出分数。这种限制可能会降低信号的预测精度。不建议存在信号退化的严重限制，即小于传统电话带宽（300- 3400hz） 。
  3. PESQ-WB是评估宽带语音条件的主观实验的背景下预测主观意见，即音频带宽从50赫兹扩展到7000赫兹的信号。这意味着，由于不同的实验环境，无法直接比较宽带扩展产生的分数和基线[ITU-T P862]或[ITU-T P862.1]产生的分数。

　　基本的P.862模型提供的原始分数在–0.5到4.5之间。 [ITU-T P.862]的PESQ-WB包括一个映射函数，输出的也是映射值，该函数允许与主观评价的MOS得分进行线性比较，这些主观实验包括音频带宽为50-7000 Hz的宽带语音条件。 这意味着由于实验环境的不同，无法直接比较PESQ-WB产生的分数和基线[ITU-T P.862]或[ITU-T P.862.1]产生的分数。 PESQ-WB中使用的输出映射函数定义如下：

$$y=0.999+\frac{4.999-0.999}{1+e^{-1.3669x+3.8224}}$$

其中$x$是原模型输出。

　　[ITU-T P.862]的附件A中给出了了PESQ-WB的宽带扩展的ANSI-C参考实现。

感知客观语音质量评估 (POLQA)

POLQA度量方法授权给了epticom公司，只有该公司授权的机构才能使用，我总结在这就是让大家了解一下，反正我们都用不了，哈哈

　　ITU P.863建议书提供了一种客观评价方法：感知客观语音质量评估 (Perceptual objective listening quality prediction, P.OLQA)， ITU-T P.863建议书支持两种操作模式，一种用于窄带 (NB, 300Hz-3.4kHz)，一种用于全带 (FB, 20Hz-20kHz)。

　　可以应用到全频带语音编解码器(例如，OPUS，增强语音服务(EVS))。比较参考信号X(t)和退化信号Y(t)，其中Y(t)是通过通信系统传递X(t)的结果，人类听觉系统中音频信号的心理物理表征，

　　ITU-T P.863算法消除了参考信号中的低水平噪声，同时对退化输出信号中的噪声也进行了部分抑制。

　　一个好的客观质量测量应该与多个不同的主观实验有很高的相关性。在实践中，使用ITU-T P.863算法，回归映射通常几乎是线性的，在日常实践中，不需要对客观分数进行特殊映射，因为ITU-T P.863分数已经映射到MOS尺度，反映了大量单独数据集的平均值。

　　POLQA结果主要是模型平均意见得分（MOS），涵盖从1（差）到5（优秀）的范围。在全频带模式下得分为MOS-LQO 4.80，在窄带模式下得分为MOS-LQO 4.5。这反映了一个事实，即不是所有的主观测试参与者都会给最高的评级，即使是不降级的参考。 

ViSQOL

【文献】

【代码】https://github.com/google/visqol (不要去下载 Releases，直接clone，Releases里面是打包好的老版本，使用的过程中会出现一些问题，clone能下到最新的版本)

【关键字】有参考，主要用于评价VoIP语音传输质量

　　ViSQOL(Virtual Speech Quality Objective Listener) 使用参考和测试语音信号之间的频谱时间相似性度量 建模人类语音质量感知。该度量被特别设计为与VoIP传输相关的质量问题的健壮性。论文描述了该算法，并与ITU-T标准度量PESQ和POLQA对VoIP常见问题的质量预测进行了比较，这些问题包括

  • 时钟漂移 (clock drift)
  • 相关的时间翘曲 (associated time warping)
  • 播放延迟 (playout delays)

　　结果表明，ViSQOL和POLQA显著优于PESQ，其中ViSQOL与POLQA具有较好的竞争优势。实验对各种质量缺陷的性能进行了基准测试，包括VoIP降级、各种背景噪声类型、语音增强方法和信噪比水平。结果和随后的分析表明，在某些VoIP条件下，ViSQOL和POLQA都存在一些性能缺陷和感知质量预测不足。两者都比PESQ或更微不足道的距离度量具有更广泛的应用和对条件的鲁棒性。所以ViSQOL在预测VoIP语音质量方面也只是提供了一个有用的替代方案。

WARP-Q

【论文】WARP-Q: Quality Prediction For Generative Neural Speech Codecs

【代码】https://github.com/wjassim/WARP-Q

【关键词】有参考，主要用于评估编码语音质量

　　语音编码已被证明可以使用波形匹配或参数重建来实现良好的语音质量。对于非常低的比特率流，最近开发的生成语音模型可以从标准参数编码器的比特流中以低于 3 kb/s 的速度重建高质量的宽带语音。生成式编解码器基于来自 DNN 和参数输入的合成语音生成高质量语音。但是，现有的客观语音质量模型（例如 ViSQOL、POLQA）不能用于从生成模型准确评估编码语音的质量，因为它们基于主观听力测试结果中不明显的信号差异进行惩罚。

　　我们提出了 WARP-Q 度量，WARP-Q（生成神经语音编解码器的质量预测）是感知语音质量的客观、完整的参考指标。它使用子序列动态时间扭曲 (SDTW) 算法作为参考（原始）和测试（降级）语音信号之间的相似性来生成原始质量分数。它旨在预测由低比特率语音编码器处理的语音信号的质量分数。

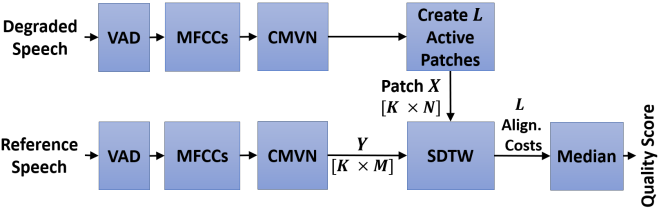
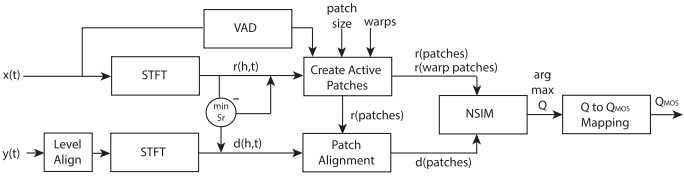
图 1：WARP-Q 度量的框图

WARP-Q 度量的算法由四个处理阶段组成：

  • 预处理：使用语音活动检测 (VAD) 算法检测和删除来自参考和降级信号的无声非语音片段。
  • 特征提取：首先生成参考信号和退化信号的梅尔频率倒谱系数 (MFCC) 表示。然后使用倒谱均值和方差归一化 (CMVN) 对获得的 MFCC 表示进行归一化，以便它们具有相同的分段统计数据（零均值和单位方差）。
  • 相似度比较：WARP-Q使用SDTW算法来估计MFCC域中参考退化信号之间的相似度。它首先将退化信号的归一化 MFCC 划分为多个$L$补丁。对于每个退化的补丁$X$，SDTW 算法然后计算$X$参考 MFCC 矩阵之间的累积对齐成本$Y$。累积对齐成本的计算基于累积对齐成本矩阵$D(X, Y)$及其$P^*$在$X$和之间的最佳路径$Y$。图 2 显示了此阶段的示例。

图2：基于sdtw的累计成本和两个信号之间的最优路径。

(a)以6kb /s的速度从一个WaveNet编码器获得的参考信号及其相应的编码版本的图(从VAD阶段获得)，

(b)两个信号的归一化MFCC矩阵，

(c)基于SDTW的累计对齐代价矩阵$D(X,Y)$及其在参考信号的MFCC矩阵$Y$与退化信号的MFCC矩阵提取的patch $X$之间的最优路径$P^*$图。并给出了最优指标($a^*$和$b^*$)。X对应于小波网信号(用绿色突出显示)的一个短段(2秒长)。

  • 子序列分数聚合：最终的质量分数由所有对齐成本的中值表示。

　　使用波形匹配、基于参数和生成神经声码器的编解码器以及信道和环境噪声的评估表明，与传统指标相比，WARP-Q 对新型编解码器具有更好的相关性和编解码器质量排名，以及捕获其他类型退化的多功能性，例如附加噪声和传输通道退化。

　　结果表明，虽然 WARP-Q 是一个建立在完善的语音信号处理特征和算法上的简单模型，但它解决了可应用于生成神经编解码器的语音质量模型的未满足需求。

综合客观语音质量 (composite)

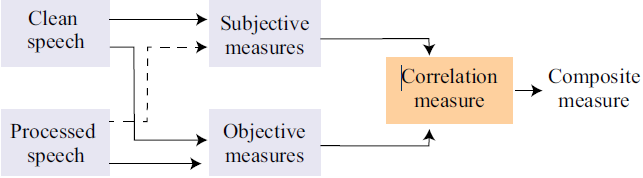
　　综合客观语音质量(Composite Objective Speech Quality，composite)度量是将现有的客观度量结合起来，形成一个新的度量。理想情况下，我们希望结合出与主观评价高度相关的客观评价度量方法，同时捕捉增强信号中出现的失真的不同特征。除了尝试不同的组合并评估产生的相关性之外，没有直接的方法可以选择用于复合度量的最佳客观度量子集。在不同的噪声失真条件和处理下，计算每个客观测量值与主观得分的相关性。然后采用线性回归分析或非线性技术将客观得分映射为主观得分。图5显示了复合度量的基本概念。

　　最近，Hu和Loizou提出了一种这样的复合度量来评价语音增强算法，即在客观语音评价指标上使用多元线性回归分析和多元自适应回归样条(multivariate adaptive regression splines, MARS)。该方法从三个不同的角度对增强语音的质量进行评估。他们是

  1. 语音的信号失真单独使用5点刻度($C_{sig}$) [1-非常不自然，2-相当不自然，3-有点自然，4-相当自然，5-非常自然]
  2. 单独的背景噪音使用5个背景干扰等级($C_{bak}$) [1-非常干扰，2-有点干扰，3-明显但不干扰，4-有点明显和5-不明显]
  3. 整体质量($C_{ovl}$) [1-差, 2-一般, 3-公平, 4-好, 5-非常棒]。

　　$C_{sig}$值越高，$C_{bak}$值越高，$C_{ovl}$值越高，信号失真度越低，背景干扰越低，语音质量越好。这些值是通过将以下现有的客观测量值线性组合得到的：

$$C_{s i g}=3.093-1.029 \mathrm{LLR}+0.603 \mathrm{P} \mathrm{ESQ}-0.009 \mathrm{~W} \mathrm{SS}$$

$$C_{b a k}=1.634+0.478 \mathrm{P} \mathrm{ESQ}-0.007 \mathrm{~W} \mathrm{SS}+0.063 \mathrm{segSN} \mathrm{R}$$

$$C_{ovl}=1.594+0.805 \text {PESQ }-0.512 \mathrm{LLR}-0.007 \mathrm{~WSS}$$

其中LLR、P ESQ、W SS、segSNR分别表示对数似然比、语音质量感知评价、加权斜率谱距离和分段信噪比。最终的目标评分值在1到5之间，像MOS。该测量得到的MOS值是基于ITU-T P.835标准。

import pysepm

pysepm.composite(clean_speech, enhanced_speech, fs)
# (1.0, 1.5970461451303148, 1.0)

基于神经网络的语音质量度量

由于深度学习的火热，也有部分人利用深度网络评估语音质量。这类方法都比较简单，因为使用的深度网络可以自动进行特征提取，因此这类方法直接将梅尔频谱系数或者MFCC直接送入模型即可。

AutoMOS

QualityNet

NISQA

【论文】

【代码】https://github.com/gabrielmittag/NISQA

【关键字】无参考、评估超宽带语音质量

　　近年来，通过将可用音频带宽从窄带扩展到宽带，再到超宽带，语音通信网络的质量得到了显著提高。这种带宽扩展标志着我们从普通的老式电话服务中所知道的典型的沉闷声音的结束。提高语音质量的另一个原因是全数字分组传输。但是，到目前为止，没有一个语音质量预测模型能够在没有清晰参考信号的情况下估计超宽带质量。

　　NISQA是一种非侵入式(non-intrusive，也可以理解为无参考)语音质量评估模型。

  • 在老版本中：该模型主要用于预测超宽带语音传输的质量。能够准确预测Opus、EVS等现代编解码器的丢包隐藏质量影响。
  • 在新版本中：模型添加了 影响语音质量的四个维度(噪声、着色(Coloration)、不连续和响度 )的客观评价

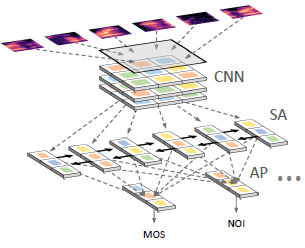
新版NISQA模型结构

MOSNet

　　现有的语音音色转换(voice conversion，VC)客观评价指标并不总是与人的感知相关。因此，用这种准则训练VC模型可能不能有效提高转换语音的自然度和相似度。该论文提出了基于深度学习的评估模型来预测转换语音的人类评分。我们采用卷积神经网络和循环神经网络模型来建立一个平均意见评分(MOS)预测器，称为MOSNet。在2018年语音转换挑战(Voice Conversion Challenge, VCC)的大规模听力测试结果上测试了所提出的模型。实验结果表明，所提出的MOSNet的预测得分在系统级与人类的MOS评分高度相关，而在话语级与人类的MOS评分相当相关。同时，我们对MOSNet进行了改进，对相似度评分进行了预测，初步结果表明，预测的评分与人类评分也有相当的相关性。这些结果证实了所提出的模型可以作为计算评估器来测量VC系统的MOS，以减少昂贵的人力评价的需要。

DNSMOS

深度感知音频度量(DPAM)

DPAM

　　在这项工作中，我们构建了一个度量，通过拟合一个深度神经网络到一个新的大数据集的众包人类判断。受试者被提示回答一个直接、客观的问题：两段录音是否相同？这两端语音是通过各种干扰算法生成的，包括噪声、混响和压缩伪影；探测扰动空间的目的是有效识别主体的刚好可察觉差异 (JND) 水平。 我们表明，由此产生的学习度量与人类判断进行了很好的校准，优于基线方法。 由于它是一个深度网络，度量是可微的，使其适合作为其他任务的损失函数。 因此，通过主观成对比较来衡量，简单地用我们的度量替换现有损失（例如，深度特征损失）可以显着改善去噪网络。

CDPAM

 　　一种基于对比学习的多维深度感知音频相似度度量 (CDPAM)是一种建立在 DPAM 基础上并对其进行改进的指标。使用三个关键思想：(1) 对比学习、(2) 多维表示学习、(3) 三元组学习。对比学习是一种自我监督学习的形式，它用合成（因此是无限的）数据来增强一组有限的人类注释：对应该被视为不同（或不相同）的数据的扰动。我们使用多维表示学习来分别建模内容相似性（例如说话者或话语之间）和声学相似性（例如录音环境之间）。对比学习和多维表示学习的结合使 CDPAM 能够更好地概括具有有限人类注释的内容差异（例如看不见的说话者）。最后，为了进一步提高对大扰动（远远超出 JND）的鲁棒性，我们收集了基于三元组比较的判断数据集，询问受试者：A 还是 B 更接近参考 C？

　　将这个指标添加到现有的语音合成和增强方法中会产生显着的改进，这是通过客观和主观测试来衡量的。

训练架构：

(a)、我们首先使用对比学习训练一个音频编码器

(b)、在JND数据上训练loss-net

(c)、最后，我们在新收集的三元组比较数据集上微调损失网络

MBNet

　　据我们所知，对于一个语音来说，之前的所有作品都只使用不同法官的多个分数的平均值作为训练目标，而丢弃了每个法官的分数，没有很好地利用宝贵的 MOS 训练数据。在本文中，我们提出了 MBNet，一个具有平均子网和偏置子网的 MOS 预测器，以更好地利用 MOS 数据集中的每个判断分数，其中平均子网用于预测每个话语的平均分数，类似于以前的工作，和偏差子网来预测偏差分数（平均分数和每个评委得分之间的差异）并捕捉每个评委的个人偏好。实验表明，与仅利用平均得分进行训练的 MOSNet 基线相比，MBNet 在 VCC 2018 数据集上将系统级 spearmans 等级相关系数 (SRCC) 提高了 2.9%，在 VCC 2016 数据集上提高了 6.7%。

 

XLS-R

  • 【代码】https://github.com/lcn-kul/xls-r-analysis-sqa

 

 

 

 

语音可懂度度量

语音可懂度的评估大致可以分为基于清晰度指数、基于语言传输指数和基于相干性指数三类，我们今天先介绍第一类。

语音可懂度评估(一)——基于清晰度指数的方法

短时客观可懂度(STOI)

 　　STOI 反映人类的听觉感知系统对语音可懂度的客观评价，STOI 值介于0~1 之间，值越大代表语音可懂度越高，越清晰。

from pystoi import stoi

stoi_score = stoi(label, logits, fs_sig=16000)

连贯性和语音可懂度指数(CSII)

Coherence and speech intelligibility index (CSII)

import pysepm

pysepm.csii(clean_speech, enhanced_speech, fs)
# (0.527623436040412, 0.2437425452887004, 0.010118033728508934)

归一化协方差度量(NCM)

Normalized-covariance measure (NCM)

import pysepm

pysepm.ncm(clean_speech, enhanced_speech, fs)

语音去混响度量

 

import pysepm

pysepm.srmr(enhanced_speech, fs)

语音混响调制能量比(SRMR)

SDR

源信号失真比(Source to Distortion Ratio, SDR)表示信号整体的失真情况

SIR

源信号干扰比(Source to Interferences Ratio, SIR)表示抑制干扰成分的能力

SAR

人造误差成分（Signal to Artifacts Ratio, SAR）表示了经算法处理生成的人造噪音的情况

 

回声消除中的客观度量

信号回声比 (Signal to echo ratio, SER)

$$SER=10\log_{10}\frac{E\{s^2(n)\}}{E\{d^2(n)\}}$$

其中

  • E是统计 期望操作(平均操作)
  • $s(n)$是近端语音
  • $d(n)$是远端回声
def SER(near_speech, far_echo):
    """signal to echo ratio, 信号回声比
    :param near_speech: 近端语音
    :param far_echo: 远端回声 
    """
    return 10*np.log10(np.mean(near_speech**2)/np.mean(far_echo**2))

回声损失增强 (Echo Return Loss Enhancement, ERLE)

　　回波损失增强(ERLE)通常用于评估系统在 没有近端信号 的 单通话情况下 的回声抑制。ERLE的公式：

$$ERLE(dB)=10\log_{10}\frac{E\{y^2(n)\}}{E\{\hat{s}^2(n)\}} $$

其中E是统计 期望操作，$y(n)$是麦克风信号，$\hat{s}(n)$是估计的近端语音信号。

def compute_ERLE(mic_wav, predict_near_end_wav):
    """ 
    :param mic_wav: 麦克风信号(y) = 近端语音(s) + 远端语音回声(s) + 噪声(v)
    :param predict_near_end_wav: 估计的近端语音信号 \hat{s}
    麦克风信号
    """
    mic_near = np.mean(mic_wav**2)
    predict_near_end_wav = np.mean(predict_near_end_wav**2)
    ERLE = 10 * np.log10(mic_near/predict_near_end_wav)
    return ERLE

　　ERLE的得分越高，代表回声消除系统越好。

为了评估系统在双讲情况下的性能，通常采用PESQ (语音质量感知评价)或STOI (短时语音可懂度)，他是通过将估计的近端语音和仅在双讲通话期间真实的近端语音进行比较得到的。PESQ评分范围为-0.5 ~ 4.5，分数越高质量越好。STOI评分范围为0~1，分数越高越好。

语音合成中的客观度量

在语音合成领域，研究的比较少，论文中常常通过展示频谱细节，计算MCD(mel cepstral distortion)等方法作为客观评价。

 有利用P.563做合成语音质量评估的尝试：

【论文】2010_Synthesized speech quality evaluation using ITU-T P. 563

识别错误率

总结

　　在本文中，简要回顾了可用于评估嘈杂语音增强算法的各种主观和客观质量度量。 客观测量主要用于算法开发阶段，用于调整各种参数。 主观测量通常可用于无法获取参考语音信号的实时应用中。 一般来说，客观测量没有考虑原始语音嘈杂的情况。 语音增强算法可能会产生比输入的嘈杂语音在感知上增强的语音。 客观措施应考虑这种情况。 这篇综述主要集中在语音增强算法的质量方面。 类似地，文献中有几种可懂度特定的主观和客观度量。 我们未来的研究将集中在这方面。

　　语音质量评估对给予了语音一个定量指标，对语音质量的评价（Audio Quality Assessment）其实是一个多年以来得到了深入研究的问题。大致可以分为需要标准信号的无参考（Non-intrusive）和有参考（instrusive）方法。无参考语音质量评估在实时通讯领域出现了许多传统和深度学习方法，

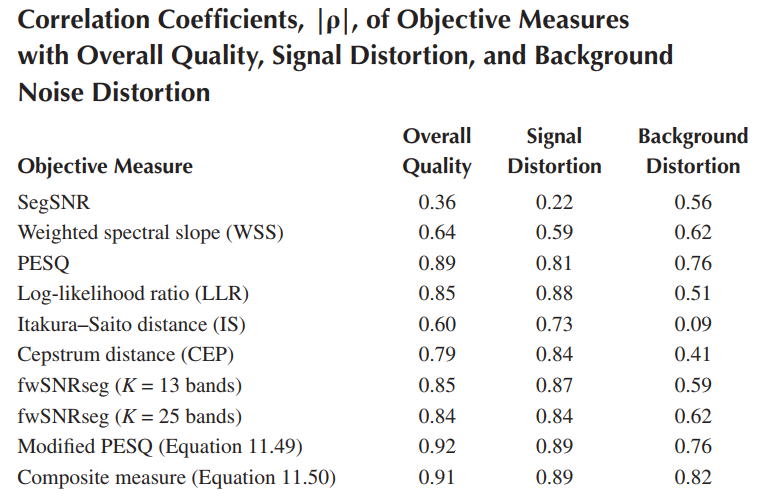
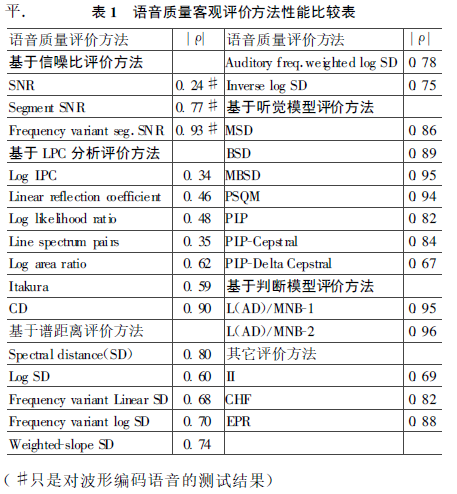
　　大多数语音客观评价标准都关注在语音信号的失真程度，较少从人类的听觉去分析，不同评价标准和真实情况的相关系数如下表所示。

使用皮尔逊相关系数(Pearson’s correlation coefficient)和标准差的误差 来评价主观评价得分与客观评价得分之间的相关性：

皮尔逊相关系数$\rho$公式表达为($\rho$值越接近于1，代表客观评价与主观评价的相关性越高，客观度量方法的性能越好)：

https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.pearsonr.html

$$\rho=\frac{\sum_{i}\left(o_{i}-\bar{o}\right)\left(s_{i}-\bar{s}\right)}{\sqrt{\sum_{i}\left(o_{i}-\bar{o}\right)^{2}} \sqrt{\sum_{i}\left(s_{i}-\bar{s}\right)^{2}}}$$

其中

  • $i$：条件语音索引
  • $s$：主观评价得分(subjective quality rating，MOS)
  • $o$：客观评价得分(objective metric score)
  • $\bar{s}$：$s$的均值
  • $\bar{o}$：$o$的均值

标准差的误差$\hat{\sigma}_{e}$公式表达为（$\hat{\sigma}_{e}$越小，代表算法的性能越好）:

$$\hat{\sigma}_{e}=\hat{\sigma}_{s} \sqrt{1-\rho^{2}}$$

其中：

$\hat{\sigma}_{s}$：主观评价得分的标准差

$\rho$：皮尔逊相关系数

斯皮尔曼等级相关(Spearman rank correlation)

 https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.spearmanr.html

参考

【CSDN文章】语音压缩算法测评及质量评估

【CSDN文章】PESQ语音质量测试

【CSDN文章】音频频率和体验知识汇总

【CSDN文章】语音压缩算法测评及质量评估

【博客园文章】语音质量评估

【书籍】Quality of Synthetic Speech: Perceptual Dimensions, Influencing Factors, and Instrumental Assessment (T-Labs Series in Telecommunication Services)

【ITU】P.800.1 : Mean opinion score (MOS) terminology

【论文】语音质量客观评价方法研究进展。陈国, 胡修林, 张蕴玉, 朱耀庭(华中科技大学电子与信息工程系)

【论文】An Overview of Subjective and Objective Quality Measures for Noisy Speech Enhancement Algorithms

【代码】speech-mos （基于深度学习，使用音频频谱图和 ConvNet 进行非侵入式语音质量评估）

【代码】利用MOS预测的自监督表示

视频质量度量指标

Voice quality metrics：包含一组用于在不同语音质量估计指标（如 PESQ MOS、MOS LQO、R-factor）之间进行转换的函数。

后续工作（以下均有论文+代码）：

Fr\'echet 音频距离：评估音乐增强算法的指标

使用生成对抗网络比较音频合成的表示

基于神经网络的实时语音增强的加权语音失真损失

基于掩码的语音增强中神经网络的组件损失

用于并行语音合成的频谱能量距离

通用音频表示的对比学习

iMetricGAN：使用基于生成对抗网络的度量学习增强噪声语音的清晰度

MetricGAN：用于语音增强的基于生成对抗网络的黑盒度量分数优化

Perceptimatic：无监督子词建模的人类语音感知基准

具有幅度和时间谱近似损失的说话人提取神经网络的优化

客观和主观的言语质量评估帕金森言语

基于Wasserstein距离的语音感知丢失增强感知质量

SRMR 工具箱

Speech-measure-SDR-SAR-STOI-PESQ

posted @ 2019-09-11 17:02  凌逆战  阅读(26338)  评论(11)    收藏  举报