Möbius inversion

莫比乌斯函数 \(\mu\)

定义

动摩擦因数，\(\mu=\dfrac{f}{N}\) ，（确信）。

当 \(d=1\) 时，\(\mu(d)=1\)。

其他时候，只要 \(d\) 中含有平方因子，那么 \(\mu(d)=0\)。否则 \(\mu(d)=(-1)^k\)， \(k\) 为 \(d\) 本质不同的质因子个数。

性质

• \(\mu*\textbf{1}=\varepsilon\)，好吧，其实这才是她的定义。简单证明一下：

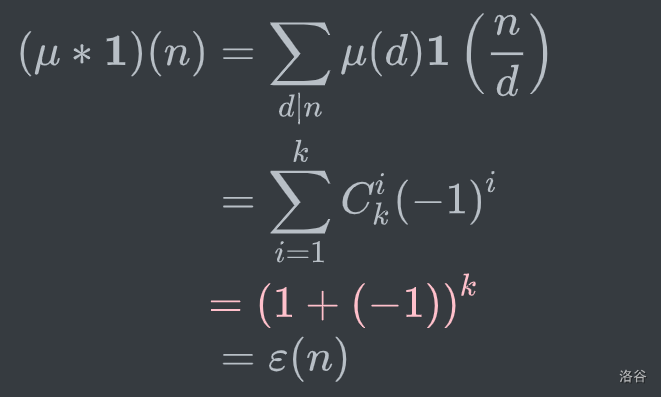
挺显然的，就是注意，\(\color{pink}{\text{pink }}\)部分用了二项式定理。

容易发现仅当 \(k=0\)，即 \(n=1\) 时，结果才为 \(1\)。所以结果就是 \(\varepsilon(n)\)。

莫比乌斯反演

设 \(f,g\) 为两个数论函数。

若 \(f=g*\textbf{1}\)，则有 \(g=f*\mu\)。结合其性质，我们发现这是显然的。

若 \(f(n)=\sum_{n\mid d}g(d)\)，则有 \(g(n)=\sum_{n\mid d}\mu\left(\frac{d}{n}\right)f(d)\)。

证明：

令 \(k=\dfrac{d}{n}\)，则有

\[\sum_{n\mid d}\mu\left(\frac dn\right)f(d)=\sum_{k=1}^{+\infty}\mu(k)f(nk)=\sum_{k=1}^{+\infty}\mu(k)\sum_{nk\mid t}g(t) \]

交换 \(n,k\)，有

\[\sum_{k=1}^{+\infty}\mu(k)\sum_{nk\mid t}g(t)=\sum_{n\mid t}g(t)\sum_{k\mid \frac{t}{n}}\mu(k) \]

在「性质」中已经证明，只有 \(\dfrac{t}{n}=1\)，结果才为 \(1\)，否则为 \(0\)。

那么最终结果就是 \(g(n)\)。

数论分块

推式子固然可以推了，但是时间复杂度？代码？

主要用于解决含有 \(\left\lfloor \dfrac{n}{i}\right\rfloor\) 的求和式。

由于 \(\left\lfloor \dfrac{n}{i}\right\rfloor\) 单调不增，故存在区间 \([l,r]\)，满足 \(\left\lfloor\dfrac ni\right\rfloor=\left\lfloor\dfrac nj\right\rfloor(i,j\in[l,r])\)。

对于一个 \(i\)，最大的 \(j=\left\lfloor\dfrac n{\left\lfloor\dfrac ni\right\rfloor}\right\rfloor\)。

证明：

\[\left\lfloor\dfrac ni\right\rfloor\le \dfrac ni \]

\[\Longrightarrow \left\lfloor\dfrac n{\left\lfloor\dfrac ni\right\rfloor}\right\rfloor\ge\left\lfloor\dfrac n{\dfrac ni}\right\rfloor=\left\lfloor i\right\rfloor=i \]

\[i\le \left\lfloor\dfrac n{\left\lfloor\dfrac ni\right\rfloor}\right\rfloor \]

所以 \(j=\left\lfloor\dfrac n{\left\lfloor\dfrac ni\right\rfloor}\right\rfloor\)。

时间复杂度是 \(O(\sqrt{n})\) 级别的。

P1403 [AHOI2005]约数研究

求 \(\displaystyle \sum _{i=1}^n d(i)\)。

考虑 \(i\) 的贡献，为 \(\left\lfloor\dfrac{n}{i}\right\rfloor\)。

答案即为 \(\displaystyle \sum _{i=1}^n \left\lfloor\dfrac{n}{i}\right\rfloor\)。

代码

P2261 [CQOI2007]余数求和

求 \(\displaystyle \sum _{i=1}^n k \bmod i\)

\(k\bmod i=k-i\times \left\lfloor\dfrac k i\right\rfloor\)。

\(\displaystyle \sum _{i=1}^n k \bmod i=n\times k- \sum _{i=1}^n i\times \left\lfloor\dfrac k i\right\rfloor\)。

这个 \(i\) 是一个等差数列。依旧可以数论分块。

代码

P2424 约数和

求 \(\displaystyle \sum_{i=x}^y \sigma(i)\)

首先是一个前缀和。然后考虑：

\(\displaystyle\sum_{i=1}^{n}\sigma(i)=\sum_{i=1}^n \sum_{k\mid i} k=\sum_{k=1}^n\sum_{k\mid i}k[i\le n]=\sum_{k=1}^{n}k\times \left\lfloor\dfrac{n}{k}\right\rfloor\)

代码

P2260 [清华集训2012]模积和

求 \(\displaystyle \sum_{i=1}^n\sum_{j=1}^m (n\bmod i)(m\bmod j)[i≠j]\bmod 19940417\)

还是比较简单的。不妨假设 \(n<m\)。

首先把式子拆成两部分： \(\displaystyle \sum_{i=1}^n\sum_{j=1}^m (n\bmod i)(m\bmod j)-\sum_{i=1}^n (n\bmod i)(m\bmod j)\)。

先考虑左边。

把 \(n\bmod i\) 移出来，并运用余数求和的思路，那么结果就是 \(\displaystyle \sum_{i=1}^n \left(n-i\times \left\lfloor\dfrac{n}{i}\right\rfloor\right)\times \sum_{j=1}^m \left(m-i\times \left\lfloor\dfrac{m}{j}\right\rfloor\right)\)，可以数论分块。

然后是右边，同样的思路： \(\displaystyle\sum_{i=1}^n\left(n-i\times \left\lfloor\dfrac{n}{i}\right\rfloor\right)\times\left(m-i\times \left\lfloor\dfrac{m}{i}\right\rfloor\right)=\sum_{i=1}^n\left(nm-n\left\lfloor\dfrac mi\right\rfloor-m\left\lfloor\dfrac ni\right\rfloor-i^2\times\left\lfloor\dfrac{m}{i}\right\rfloor\left\lfloor\dfrac{n}{i}\right\rfloor\right)\)，数论分块即可。

\(i^2\) 怎么处理？小学就学过的 \(\displaystyle \sum_{i=1}^n i^2=\dfrac{n(n+1)(2n+1)}{6}\)。

代码,注意取模。

反演题目

在这里