题解-CF1156D 0-1-Tree

CF1156D 0-1-Tree

题意

• 给定一颗 \(n\) 个点的边权为 \(0\) 或 \(1\) 的树。
• 定义 合法路径 \((x,y)\) \((x\not= y)\) 为，满足从 \(x\) 走到 \(y\) 一旦经过边权为 \(1\) 的边，就不能再经过边权为 \(0\) 的边的路径。
• 求合法路径个数。
• \(2\le n \le 2 \times 10^5\) 。

分析

前置芝士：并查集

有 \(O(n)\) 的换根 DP 做法，可惜我不会。

但是 \(O(n\log n)\) 的并查集又好打，又好理解，何乐而不为？

首先，如何求合法路径个数？

我们可以枚举树上的所有结点，不妨记通过当前节点 \(i\) 的路径数量为 \(num_i\) 。最后的答案即是 \(\sum_{i=1}^{n} num_i\) 。

如何避免重复算？

我们考虑并查集。先不着急，一步步来。

我们发现合法路径的边权一定是

• 情况 \(1\) ：全为 \(0\) ，
• 情况 \(2\) ：全为 \(1\) ，
• 情况 \(3\) ：前一部分全为 \(0\) ，后一部分全为 \(1\) ，

上述三者之一。

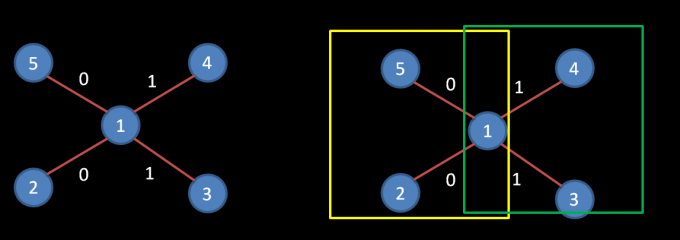
放一张图。

我们不妨用一个并查集维护所有边权为 \(0\) 的边组成的连通块，如上图黄色部分。对于边权为 \(1\) 的边同理，上图绿色部分。记维护 \(0\) 边的并查集为 \(a\) ， \(1\) 边的为 \(b\) 。用 \(sza_i\) 表示点 \(i\) 所在边权为 \(0\) 的联通块大小， \(szb_i\) 同理。

例：图中 \(sza_1=3,szb_1=3\) 。

那么， \(num_i=sza_i\times szb_i - 1\) 。

这里的 \(num_i\) 为， \(i\) 作为所在连通块内的合法路径的某一 顶点 时的合法路径数，加上 \(i\) 作为前文情况 \(3\) 中的 \(01\) 分界点 时合法路径数的和。然后这个和可以用上面的式子表示，是一个排列组合。以上图为例，可以看作是黄色部分有 \(3\) 个点与绿色部分 \(3\) 个点的搭配。为什么是 \(3\) 而非 \(2\) ？因为此时包括分界点 \(1\) ，而当分界点被看成属于黄色时，与绿色搭配，求得即是以 \(1\) 为顶点时绿色区域内合法路径的个数。当分界点被看作属于绿色时，同理。而分界点不能与自己形成合法路径，因而要 \(-1\) 。

这样就可以避免重复 / 漏 掉某些路径。大家可以好好想想为什么加粗的字可以有效避免重复或漏算。

大致解释一下。当 \(i\) 为顶点时，假设存在一合法路径 \((i,j)\) ，则必然存在合法路径 \((j,i)\) ，而在枚举到 \(j\) 时，会计算路径 \((j,i)\) ，所以不会漏，而 \(i,j\) 在同一连通块，不可能在枚举到其他点时也统计上这个路径，所以不会重。当 \(i\) 为分界点时，很显然，每种满足情况 \(3\) 的路径都 有且仅有一个分界点 ，故而既不会重，也不会漏。

代码

有一些小细节，放在代码注释里。

#include<bits/stdc++.h>
using namespace std;
int n,cnt;
int fa[200005],fb[200005];
int sza[200005],szb[200005];
//a-1 b-0
int finda(int x)
{
	return fa[x]==x?x:fa[x]=finda(fa[x]);
}
int findb(int x)
{
	return fb[x]==x?x:fb[x]=findb(fb[x]);
}
inline int read()
{
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();}
	while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
	return x*f;
}
int main()
{
	n=read();
	for(int i=0;i<=n;i++)	fa[i]=fb[i]=i,szb[i]=sza[i]=1;
	for(int i=1;i<n;i++)
	{
		int u=read(),v=read(),w=read();
		if(w==1)
		{
			int p=finda(u),q=finda(v);
			fa[p]=q;
			sza[q]+=sza[p];//注意，fa[p]=q 表示 p 的祖先是 q ，所以 sz 是修改 q 的而非 p 的。
		}
		if(w==0)
		{
			int p=findb(u),q=findb(v);
			fb[p]=q;
			szb[q]+=szb[p];//同上
		}//这里的 merge 写的有点丑，不过问题不大
	}
	long long ans=0;
	for(int i=1;i<=n;i++)
	{
		int p=finda(i),q=findb(i);
		ans=ans+1ll*sza[p]*szb[q]-1;
	}
	printf("%lld\n",ans);
	return 0;
}

完结撒花~