『分块入门』学习笔记
从作者的洛谷博客转过来的
起因:今天集训 \(LJ\) 讲题的时候讲到一道题可以用分块做,就让我们课后自学分块。
然后中午就找了 \(hzwer\) 巨佬的博客自学了一下。本文仅仅是作者的学习笔记,因此讲不清楚原理,让人难以理解的东西会经常出现。请见谅。(反正也没人会看)。
大概一周更完 \(LOJ\) 上的 \(1-9\) 题,就结束了。
这就是 \(LJ\) 所谓区间修改,单点查询的模板题。
所谓数列分块就是把一个数列分成一整块一整块,以此优化算法。
这道题中,我们如果在长度为 \(n\) 的数列中每 \(m\) 个元素分成一块块,则共有 \(n/m\) 块。
这样每一次区间操作中的区间 \([l,r]\) 都是由两种类型组成的 \(\begin{cases} \text{ 1.整的分块} \\\text{ 2.整块两边的零散部分} \end{cases} \)
于是进行区间操作时,我们分成两步去做
\(\begin{cases} \text{ 1.对于整的分块直接O(1)标记} \\\text{ 2.对于整块两边的零散部分暴力} \end{cases} \)
那么,问题来了,每个分块长度是多少呢?
显然不可能是 \(1\) 或者 \(n\) 这样达不到优化算法的目的。
可以发现每次修改/查询,复杂度最坏是 \(Θ(k+m)\) 级别(\(k\) 为块数 \(m\)为分块长度)。因 \(k*m\) 是定值(\(n\)),要让 \(k+m\) 最小,就是让 \((k+m)^2\) 最小,即 \(k^2+m^2+2km\) ,根据均值不等式,\(k^2+m^2\) 最小,当且仅当 \(k=m\) \(k^2+m^2=2km\)时,所以 \(k=m=\sqrt{n}\) 。参考文章 \(->\)\(Link\)
于是贴出我们的代码
#include<bits/stdc++.h>
#define FOR(i,j,k) for(int i=(j);i<=(k);i++)
using namespace std;
int n,blo;//blo 为分块长度
int a[50001];
int bl[50001],s[50001];//bl[i]表示当前点属于第几分块,s[i]表示第i个分块统一加了几
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}//快读
inline void add(int l,int r,int c)
{
for(int i=l;i<=min(bl[l]*blo,r);i++)//区间左端不在分块的边界
a[i]+=c;
if(bl[l]!=bl[r])//不相等,说明区间右端点在另一个分块
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
a[i]+=c;
for(int i=bl[l]+1;i<=bl[r]-1;i++)//左右多出的部分都已经暴力处理完毕 ,剩下的就是分块内同加c
s[i]+=c;
}//opt=0时的加数操作
int main()
{
n=read();
blo=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
bl[i]=(i-1)/blo+1;
for(int i=1;i<=n;i++)
{
int opt=read(),l=read(),r=read(),c=read();
if(opt==0) add(l,r,c);//区间操作:[l,r]区间内加c
if(opt==1) printf("%d\n",a[r]+s[bl[r]]);//单点查询:这个点的大小为点所在的块所加的于这个点的值得和
}
return 0;
}
这道题很显然就是在 \(T1\) 的基础上,把单点询问改成了区间询问。
不完整的块,我们依旧暴力查询,那么整块呢?
可以想到,我们用 vector 存块,在预处理时,对每个块内的元素进行排序,这样就可以二分找出当前块内第一个值 \(>=c^2\) 的元素。复杂度为 \(O(nlogn+n\sqrt{n}log\sqrt{n})\)。把这些想通了就不难做了。
据说可以算出更好的块长,这里作者水平有限,就不讨论了。
丢出我们的代码。
#include<bits/stdc++.h>
#define FOR(i,j,k) for(int i=(j);i<=(k);i++)
using namespace std;
int n,blo;
int a[50005],bl[50005],An[50005];
vector <int> v[505];
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
inline void resort(int x)
{
v[x].clear();
for(int i=(x-1)*blo+1;i<=min(x*blo,n);i++)
v[x].push_back(a[i]);
sort(v[x].begin(),v[x].end());
}//重新排序,因为对于不完整的块的加法操作会破坏当前块的大小顺序。
inline void add(int l,int r,int c)
{
for(int i=l;i<=min(r,bl[l]*blo);i++)
a[i]+=c;
resort(bl[l]);
if(bl[l]!=bl[r])
{
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
a[i]+=c;
resort(bl[r]);
}
for(int i=bl[l]+1;i<=bl[r]-1;i++)
An[i]+=c;
}
inline int query(int l,int r,int x)
{
int res=0;
for(int i=l;i<=min(bl[l]*blo,r);i++)
if(a[i]+An[bl[l]]<x) res++;
if(bl[l]!=bl[r])
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
if(a[i]+An[bl[r]]<x) res++;
for(int i=bl[l]+1;i<=bl[r]-1;i++)
{
int c=x-An[i];
res+=lower_bound(v[i].begin(),v[i].end(),c)-v[i].begin();//这里一开始我是手打的二分,但不知道为何 WA 个不停,最终换回了 STL版的二分。
}
return res;
}
int main()
{
n=read();
blo=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
{
bl[i]=(i-1)/blo+1;
v[bl[i]].push_back(a[i]);
}
for(int i=1;i<=bl[n];i++)
sort(v[i].begin(),v[i].end());
for(int i=1;i<=n;i++)
{
int op=read(),l=read(),r=read(),c=read();
if(op==0) add(l,r,c);
if(op==1) printf("%d\n",query(l,r,c*c));
}
return 0;
}
这道题要询问区间内小于某个值 \(x\) 的前驱(比其小的最大元素)。
我们在上一题的基础上将代码稍微改一下即可,对于每一个询问分成两步
\(\begin{cases} \text{ 1.整的分块二分} \\\text{ 2.整块两边的零散部分暴力} \end{cases}\)
我们会发现 使用 multiset 要比 vector 好写。
为什么不用 set 可以看这个讨论
简而言之就是 set 会自动去重。
于是就可以轻松码出我们的代码
#include<bits/stdc++.h>
#define FOR(i,j,k) for(int i=(j);i<=(k);i++)
using namespace std;
int n,blo;
int a[100005];
int bl[100005],An[100005];
multiset<int> s[5005];
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
void add(int l,int r,int c)
{
for(int i=l;i<=min(bl[l]*blo,r);i++)
{
s[bl[l]].erase(a[i]);
a[i]+=c;
s[bl[l]].insert(a[i]);
}
if(bl[l]!=bl[r])
{
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
{
s[bl[r]].erase(a[i]);
a[i]+=c;
s[bl[r]].insert(a[i]);
}
}
for(int i=bl[l]+1;i<=bl[r]-1;i++)
An[i]+=c;
}
int query(int l,int r,int c)
{
int ans=-1;
for(int i=l;i<=min(bl[l]*blo,r);i++)
{
int val=a[i]+An[bl[l]];
if(val<c)ans=max(val,ans);
}
if(bl[l]!=bl[r])
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
{
int val=a[i]+An[bl[r]];
if(val<c)ans=max(val,ans);
}
for(int i=bl[l]+1;i<=bl[r]-1;i++)
{
int x=c-An[i];
multiset<int>::iterator it=s[i].lower_bound(x);
if(it==s[i].begin())continue;
--it;
ans=max(ans,*it+An[i]);
}
return ans;
}
int main()
{
n=read();blo=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
{
bl[i]=(i-1)/blo+1;
s[bl[i]].insert(a[i]);
}
for(int i=1;i<=n;i++)
{
int op=read(),l=read(),r=read(),c=read();
if(op==0) add(l,r,c);
if(op==1) printf("%d\n",query(l,r,c));
}
return 0;
}
(看这个样子一周更新不完了)
这题要求区间求和,很容易想到 开一个数组预处理一下
用 sum[i] 表示第 \(i\) 个块的元素和,An[i] 表示 第 \(i\) 个块整体所加的值
每次 add 操作 \(\begin{cases}
\text{ 1.整的分块 An 数组加 c } \\\text{ 2.整块两边的零散部分暴力,sum 数组加 c } \end{cases}\)
每次询问\(\begin{cases} \text{ 1.整的分块=元素和+整体加的值*块长} \\\text{ 2.整块两边的零散部分暴力相加即可} \end{cases}\)
不难码出 \(code\)
#include<bits/stdc++.h>
#define FOR(i,j,k) for(int i=(j);i<=(k);i++)
using namespace std;
int n,blo;
int a[50005],bl[50005];
long long sum[50005],An[50005];
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
inline void add(int l,int r,int c)
{
for(int i=l;i<=min(blo*bl[l],r);i++)
a[i]+=c,sum[bl[l]]+=c;
if(bl[l]!=bl[r])
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
a[i]+=c,sum[bl[r]]+=c;
for(int i=bl[l]+1;i<=bl[r]-1;i++)
An[i]+=c;
}
inline long long query(int l,int r)
{
long long ans=0;
for(int i=l;i<=min(blo*bl[l],r);i++)
ans+=a[i]+An[bl[l]];
if(bl[l]!=bl[r])
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
ans+=a[i]+An[bl[r]];
for(int i=bl[l]+1;i<=bl[r]-1;i++)
ans+=sum[i]+An[i]*blo;
return ans;
}
int main()
{
n=read();
blo=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
{
bl[i]=(i-1)/blo+1;
sum[bl[i]]+=a[i];
}
for(int i=1;i<=n;i++)
{
int opt=read(),l=read(),r=read(),c=read();
if(opt==0) add(l,r,c);
if(opt==1) printf("%d\n",query(l,r)%(c+1));
}
return 0;
}
明天做,今天把你谷上的 \(\textit{P2357 守墓人}\) 水掉了。
水完P3870 [TJOI2009]开关,回来更新。
因为这里的开方操作皆向下取整,故 \(n\) 次开方后结果为 \(0/1\) 。
于是考虑用一个数组记录当前整块元素是否全为 \(1/0\) 若全为 \(1/0\) 就不用再进行开方操作。
那么代码如下
#include<bits/stdc++.h>
#define FOR(i,j,k) for(int i=(j);i<=(k);i++)
using namespace std;
int n,blo;
int bl[50005],a[50005],sum[250];
bool flag[250];
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
inline void s_s(int x)
{
if(flag[x]) return ;
flag[x]=true;
sum[x]=0;
for(int i=(x-1)*blo+1;i<=x*blo;i++)
{
a[i]=sqrt(a[i]);
sum[x]+=a[i];
if(a[i]>1) flag[x]=false;
}
}
inline void add(int l,int r)
{
for(int i=l;i<=min(bl[l]*blo,r);i++)
{
sum[bl[l]]-=a[i];
a[i]=sqrt(a[i]);
sum[bl[l]]+=a[i];
}
if(bl[l]!=bl[r])
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
{
sum[bl[r]]-=a[i];
a[i]=sqrt(a[i]);
sum[bl[r]]+=a[i];
}
for(int i=bl[l]+1;i<=bl[r]-1;i++)
s_s(i);
}
inline int query(int l,int r)
{
int ans=0;
for(int i=l;i<=min(blo*bl[l],r);i++)
ans+=a[i];
if(bl[l]!=bl[r])
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
ans+=a[i];
for(int i=bl[l]+1;i<=bl[r]-1;i++)
ans+=sum[i];
return ans;
}
int main()
{
n=read();
blo=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
{
bl[i]=(i-1)/blo+1;
sum[bl[i]]+=a[i];
}
for(int i=1;i<=n;i++)
{
int op=read(),l=read(),r=read(),c=read();
if(op==0) add(l,r);
if(op==1) printf("%d\n",query(l,r));
}
return 0;
}
突然发现分块我从来没有一次写对过
吐槽:这 \(c\) 什么用都没有,怕不是 \(hzwer\) 巨佬懒得造数据了。
这里涉及插入,我们用 vector 维护分块,每 \(\sqrt{n}\) 次插入后,重构分块。
#include<bits/stdc++.h>
#define FOR(i,j,k) for(int i=(j);i<=(k);i++)
using namespace std;
int n,blo,End;
int a[100001];
vector<int> v[1001];
int tmp[200001];
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
return x*f;
}
pair<int,int> query(int x)
{
int bl=1;
while(x>v[bl].size())
x-=v[bl].size(),bl++;
return make_pair(bl,x-1);
}
inline void rebuild()
{
int top=0;
for(int i=1;i<=End;i++)
{
for(int j=0;j<v[i].size();j++)
tmp[++top]=v[i][j];
v[i].clear();
}
int len=sqrt(top);
for(int i=1;i<=top;i++)
v[(i-1)/blo+1].push_back(tmp[i]);
End=(top-1)/blo+1;
}
inline void insert(int l,int r)
{
pair<int,int> p=query(l);
v[p.first].insert(v[p.first].begin()+p.second,r);
if(v[p.first].size()>20*blo) rebuild();
}
int main()
{
n=read();
blo=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
v[(i-1)/blo+1].push_back(a[i]);
End=(n-1)/blo+1;
for(int i=1;i<=n;i++)
{
int op=read(),l=read(),r=read(),c=read();
if(op==0) insert(l,r);
if(op==1)
{
pair<int,int> p=query(r);//first-belong,second-No
printf("%d\n",v[p.first][p.second]);
}
}
return 0;
}
涉及乘法,加法运算。效仿分块1的思路,建一个 mtag 和 atag。
若当前块 \(x\) 乘 \(m_1\) 后加 \(a_1\) 再乘 \(m_2\) ,则 \(mtag_x=m_1\times m_2 ,atag_x=a_1*m_2\)
若当前块 \(x\) 乘 \(m_1\) 后加 \(a_1\) 再加 \(a_2\) , 则 \(mtag_x=m_1,atag_x=a_1+a_2\)
#include<bits/stdc++.h>
#define FOR(i,j,k) for(int i=(j);i<=(k);i++)
#define Mod 10007
using namespace std;
int a[100001],bl[100001],atag[1005],mtag[1005],L[1005],R[1005];
int n,blo;
int op,l,r,c;
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
return x*f;
}
inline void reset(int x)
{
for(int i=L[x];i<=R[x];i++)
a[i]=(a[i]*mtag[x]+atag[x])%10007;
mtag[x]=1,atag[x]=0;
}
inline void add(int l,int r,int c)
{
if(bl[l]==bl[r])
{
reset(bl[l]);
for(int i=l;i<=r;i++)
a[i]=(a[i]+c)%Mod;
return ;
}
reset(bl[l]),reset(bl[r]);
for(int i=l;i<=R[bl[l]];i++)
a[i]=(a[i]+c)%Mod;
for(int i=bl[l]+1;i<=bl[r]-1;i++)
atag[i]=(atag[i]+c)%Mod;
for(int i=L[bl[r]];i<=r;i++)
a[i]=(a[i]+c)%Mod;
}
inline void mul(int l,int r,int c)
{
if(bl[l]==bl[r])
{
reset(bl[l]);
for(int i=l;i<=r;i++)
a[i]=(a[i]*c)%Mod;
return ;
}
reset(bl[l]),reset(bl[r]);
for(int i=l;i<=R[bl[l]];i++)
a[i]=(a[i]*c)%Mod;
for(int i=bl[l]+1;i<=bl[r]-1;i++)
atag[i]=(atag[i]*c)%Mod,mtag[i]=(mtag[i]*c)%Mod;
for(int i=L[bl[r]];i<=r;i++)
a[i]=(a[i]*c)%Mod;
}
int main()
{
n=read();
blo=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=read()%Mod;
for(int i=1;i<=n;i++)
bl[i]=(i-1)/blo+1;
for(int i=1;i<=bl[n];i++)
L[i]=R[i-1]+1,R[i]=min(n,L[i]+blo-1),mtag[i]=1;
for(int i=1;i<=n;i++)
{
op=read(),l=read(),r=read(),c=read();
if(op==2) printf("%d\n",(a[r]*mtag[bl[r]]+atag[bl[r]])%10007);
if(op==1) mul(l,r,c);
if(op==0) add(l,r,c);
}
return 0;
}
然后是加强版 线段树2
这个个问题难在区间修改。
我们发现多次询问后,数列可能只剩下几段互不相同的区间了。
我们考虑使用一个数组维护每个分块是否只有一个权值\(\begin{cases} \text{ 1.只有一个:O(1)统计 } \\\text{ 2.多个:暴力统计,修改标记} \end{cases}\)
于是给出代码
#include<bits/stdc++.h>
#define FOR(i,j,k) for(int i=(j);i<=(k);i++)
using namespace std;
int a[100001],bl[100001],tag[320];
int n,blo;
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
inline void reset(int x)
{
if(tag[x]==-0x7f7f) return ;
for(int i=(x-1)*blo+1;i<=x*blo;i++)
a[i]=tag[x];
tag[x]=-0x7f7f;
}
inline int query(int l,int r,int c)
{
int ans=0;
reset(bl[l]);
for(int i=l;i<=min(bl[l]*blo,r);i++)
if(a[i]!=c) a[i]=c;
else ans++;
if(bl[l]!=bl[r])
{
reset(bl[r]);
for(int i=(bl[r]-1)*blo+1;i<=r;i++)
if(a[i]!=c) a[i]=c;
else ans++;
}
for(int i=bl[l]+1;i<=bl[r]-1;i++)
if(tag[i]!=-0x7f7f)
{
if(tag[i]!=c) tag[i]=c;
else ans+=blo;
}
else
{
for(int j=(i-1)*blo+1;j<=i*blo;j++)
if(a[j]!=c) a[j]=c;
else ans++;
tag[i]=c;
}
return ans;
}
int main()
{
n=read();
blo=sqrt(n);
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
bl[i]=(i-1)/blo+1;
for(int i=1;i<=bl[n];i++)
tag[i]=-0x7f7f;
for(int i=1;i<=n;i++)
{
int l=read(),r=read(),c=read();
printf("%d\n",query(l,r,c));
}
return 0;
}
求区间最小众数。
读入离散化。
预处理时用 \(f_{i,j}\) 表示 第 \(i\) 个整块到第 \(j\) 个整块间的众数。
开 vector 维护整块,求当前块中 \(x\) 的数量用 upper_bound - lower_bound 即可。
#include<bits/stdc++.h>
using namespace std;
int n,blo,cnt;
int a[100001],bl[100001],L[520],R[520];
int f[520][520],val[100010],num[100010];
map<int,int>mp;
vector<int> v[100010];
inline int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-') f=-1;
c=getchar();
}
while(c>='0'&&c<='9')
{
x=x*10+c-'0';
c=getchar();
}
return x*f;
}
inline void pre(int x)
{
memset(num,0,sizeof(num));
int mx=0,p=0;
for(int i=L[x];i<=n;i++)
{
num[a[i]]++;
int t=bl[i];
if(num[a[i]]>mx||(num[a[i]]==mx&&val[a[i]]<val[p]))
p=a[i],mx=num[a[i]];
f[x][t]=p;
}
}
inline int getnum(int l,int r,int x)
{
int num=upper_bound(v[x].begin(),v[x].end(),r)-lower_bound(v[x].begin(),v[x].end(),l);
return num;
}
inline int query(int l,int r)
{
int ans,mx;
if(bl[l]==bl[r])
{
ans=0,mx=0;
for(int i=l;i<=r;i++)
{
int num=getnum(l,r,a[i]);
if(num>mx||(num==mx&&val[a[i]]<val[ans]))
ans=a[i],mx=num;
}
return ans;
}
ans=f[bl[l]+1][bl[r]-1];
mx=getnum(l,r,ans);
for(int i=l;i<=R[bl[l]];i++)
{
int num=getnum(l,r,a[i]);
if(num>mx||(num==mx&&val[a[i]]<val[ans]))
ans=a[i],mx=num;
}
for(int i=L[bl[r]];i<=r;i++)
{
int num=getnum(l,r,a[i]);
if(num>mx||num==mx&&val[a[i]]<val[ans])
ans=a[i],mx=num;
}
return ans;
}
int main()
{
n=read();
blo=200;
for(int i=1;i<=n;i++)
{
a[i]=read();
if(!mp[a[i]])
{
mp[a[i]]=++cnt;
val[cnt]=a[i];
}
a[i]=mp[a[i]];//离散化
v[a[i]].push_back(i);
}
for(int i=1;i<=n;i++)
bl[i]=(i-1)/blo+1;
for(int i=1;i<=bl[n];i++)
L[i]=R[i-1]+1,R[i]=min(L[i]+blo-1,n);
for(int i=1;i<=bl[n];i++)
pre(i);
for(int i=1;i<=n;i++)
{
int l=read(),r=read();
if(l>r) swap(l,r);
printf("%d\n",val[query(l,r)]);
}
}
今天尝试用分块水题的过程中遇见了一个之前没想到过的优化。
把每个块的开头下标和结尾下标存起来,这样无论是 \(query\) 还是 \(add\) 都可以避免多次算 bl[l]*blo (bl[r]-1)*blo+1 之类的。 \(LJ\) 曾说,一道题 \(TLE\) 不是算法错误就是计算太多。
经试验效果感人


代码
#include<bits/stdc++.h>
#define FOR(i,j,k) for(int i=(j);i<=(k);i++)
using namespace std;
long long m,n;
long long blo,Min[320],Right[320],Left[320];
long long a[100001],bl[100001];
inline long long read()
{
long long x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
return x*f;
}
inline long long query(long long l,long long r)
{
long long ans=0x3f3f3f3f;
if(bl[l]==bl[r])
{
for(int i=l;i<=r;i++)
ans=min(ans,a[i]);
return ans;
}
for(int i=l;i<=Right[bl[l]];i++)
ans=min(ans,a[i]);
for(int i=Left[bl[r]];i<=r;i++)
ans=min(ans,a[i]);
for(int i=bl[l]+1;i<=bl[r]-1;i++)
ans=min(ans,Min[i]);
return ans;
}
int main()
{
memset(Min,0x3f3f3f3f,sizeof(Min));
m=read(),n=read();
blo=sqrt(m);
for(long long i=1;i<=m;i++)
a[i]=read();
for(long long i=1;i<=m;i++)
{
bl[i]=(i-1)/blo+1;
Min[bl[i]]=min(Min[bl[i]],a[i]);
}
for(long long i=1;i<=bl[m];i++)
Left[i]=Right[i-1]+1,Right[i]=min(m,Left[i]+blo-1);
for(long long i=1;i<=n;i++)
{
long long l=read(),r=read();
printf("%lld ",query(l,r));
}
return 0;
}
学了一点二维分块的皮毛。
题目:P3397 地毯
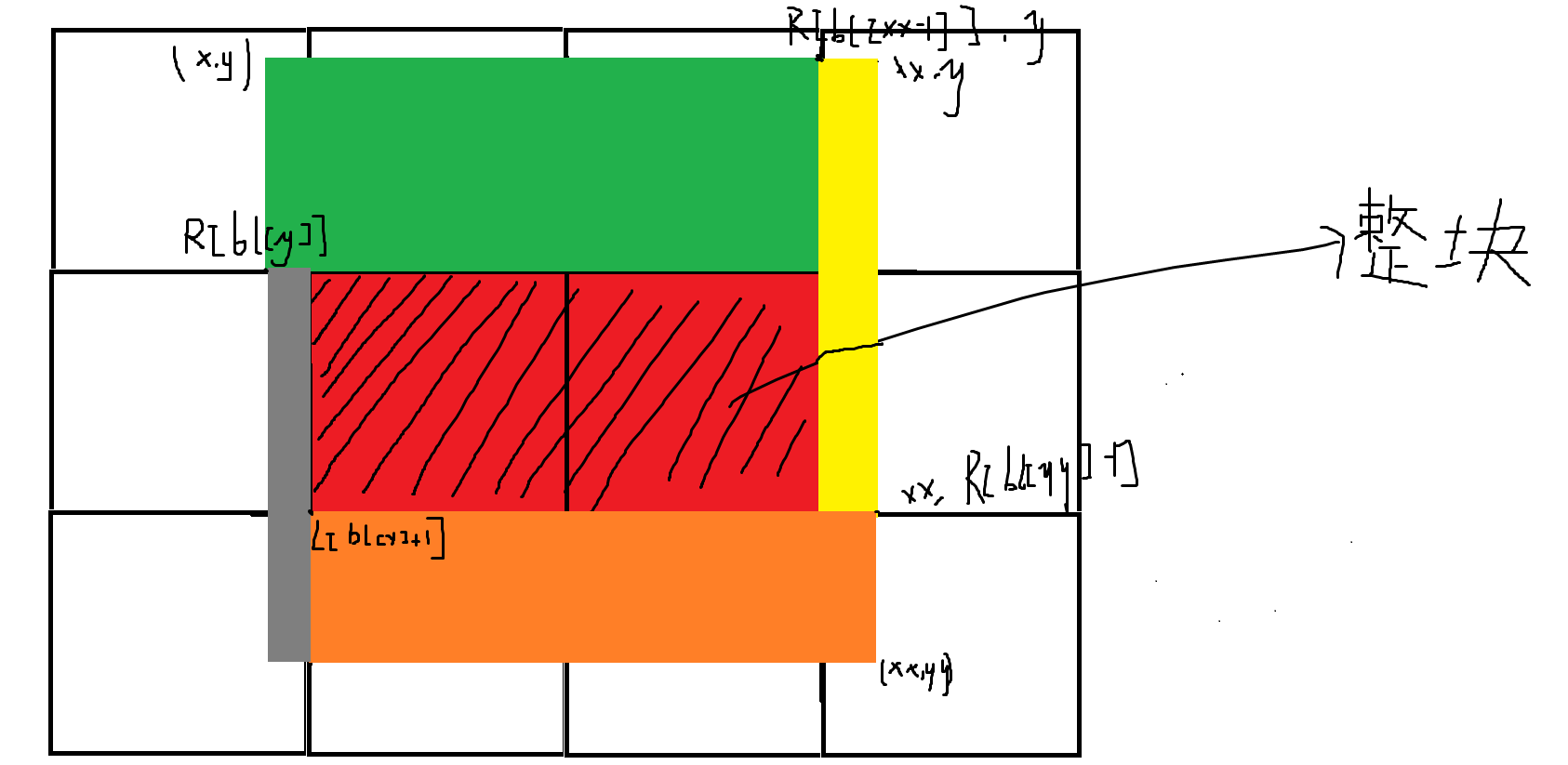
code
#include<bits/stdc++.h>
#define x1 x
#define x2 xx
#define y1 y
#define y2 yy
using namespace std;
int n,m;
int blo,L[40],R[40];
int bl[1500],atag[40][40],a[1500][1500];
inline int read()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
inline void add(int x1,int y1,int x2,int y2)
{
if(bl[x1]==bl[x2]||bl[y1]==bl[y2])
{
for(int i=x1;i<=x2;i++)
for(int j=y1;j<=y2;j++)
a[i][j]++;
return ;
}
for(int i=bl[x1]+1;i<=bl[x2]-1;i++)
for(int j=bl[y1]+1;j<=bl[y2]-1;j++)
atag[i][j]++;
for(int i=x1;i<=R[bl[x2]-1];i++)
for(int j=y1;j<=R[bl[y1]];j++)
a[i][j]++;
for(int i=L[bl[x2]];i<=x2;i++)
for(int j=y1;j<=R[bl[y2]-1];j++)
a[i][j]++;
for(int i=L[bl[x1]+1];i<=x2;i++)
for(int j=L[bl[y2]];j<=y2;j++)
a[i][j]++;
for(int i=x1;i<=R[bl[x1]];i++)
for(int j=L[bl[y1]+1];j<=y2;j++)
a[i][j]++;
}
int main()
{
n=read(),m=read();
blo=sqrt(n);
for(int i=1;i<=n;i++)
bl[i]=(i-1)/blo+1;
for(int i=1;i<=bl[n];i++)
L[i]=R[i-1]+1,R[i]=min(n,L[i]+blo-1);
for(int i=1;i<=m;i++)
{
int u=read(),v=read(),w=read(),x=read();
add(u,v,w,x);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
printf("%d ",a[i][j]+atag[bl[i]][bl[j]]);
printf("\n");
}
return 0;
}
\(To\) \(Be\) \(Continued\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号