浅说线性倍增和树上倍增
倍增
易错提醒
首先强调一下,倍增不是一种算法,它是一种思想,而像什么 RMQ 问题啊,ST 表啊,都是由倍增思想演变出来的一种算法。接下来我们来正式的接入今天的话题
什么是倍增
倍增,倍增,顾名思义,就是以一个数成倍的增长,这个数通常是2。当然也会有在不同的时候会以其他的数进行翻倍,比如3,8,16等等,但是都不常见。我们现在就先来讲讲倍增中的线性倍增。
线性倍增
倍增一般情况下就是用来求解某一区间的极值,或一个成倍增长的数。
引入——快速幂与倍增的关联
快速幂和倍增也有一点点的关联,我们知道快速幂是通过二进制分解的形式来计算的,而倍增也是构成二进制位权的方法。
区间极值问题
给定一个长度为 \(n\) 的区间,给定 \(m\) 次询问,每次询问有两个值 \(l,r\) 代表一个区间的左右端点,请给出这个区间的最大值。
上述问题就是一个区间极值问题,而区间极值问题就是 RMQ 问题,我们这里不要抛开本质的倍增而只去关注算法。我们要把两者结合起来看。
首先,如果让你去求一个区间的极值,你会怎么求?是不是只能去枚举每一段,然后求一个最大值?这样的时间复杂度是 \(O(n^2)\) ,相比之下,有点高。那么我们可以怎么弄呢?
我们这里要先了解一个二进制数的特性:所有的实数都可以被写成若干个二进制相加,也就是说,我们可以采用二进制的方式去表达每个数。基于此,我们的每段区间都可以分成若干个,长度为 \(2^k\) 的区间,那么我们只需要对在这些区间中找一个最大值不就完了?
那么我们现在的问题就转化到了如何求解每段长度为 \(2^k\) 的区间的最大值呢?和如何利用这些区间去求得每个区间的极值?
问题1——如何预处理
问题描述:如何求解每段长度为 \(2^k\) 的区间的最大值
子问题1
这里我们考虑使用动态规划。
首先我们知道,动态规划一定是从最优解到最优解,所以我们这里要先知道当前是2的多少倍,所以我们应该先枚举指数 \(i\) ,其次,我们还需要知道每一段的起点和终点,所以我们还要去枚举起点 \(j\) (注意:这里 \(j\) 的范围应该是 \(1 \le j \le n+1-2^i\) ,因为这是一个区间)
那么我们就可以得到以下代码
for (int i=1;(1<<i)<=n;i++){
for (int j=1;j+(1<<i)-1<=n;j++){
//状态转移
}
}
我们现在知道了如何枚举,接下来就是如何进行转移了。
子问题2
上面我们讲了,动态规划是从最优解到最优解,再加上我们是以2的倍数进行分段的,所以我们其实可以把当前的区间分成两个小的区间,也就是分成两个长度为 \(2^{k-1}\) 的区间,又因为我们是先枚举的指数,所以 \(2^{k-1}\) 的两个答案我们是知道的,所以我们只需要在两个答案中选一个最大的(或最小的)就行了。
只不过我们还需要知道这两段分别的起点。
这里我们可以画一个图来了解一下
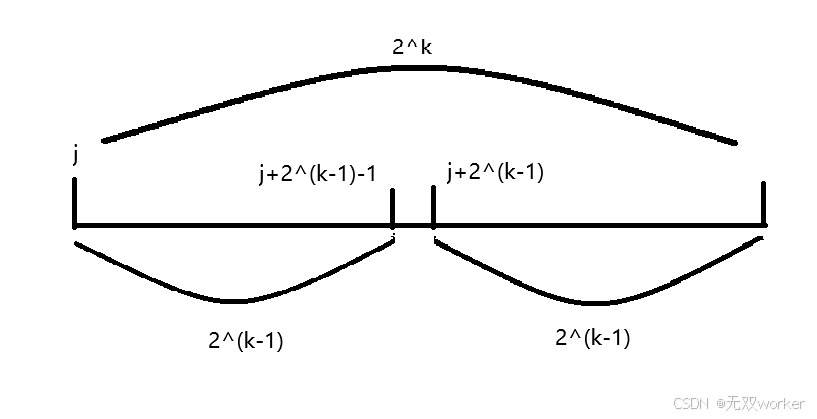
由图可见,第一段是 \(j \to j+2^{k-1}-1\) ,第二段是 \(j+2^{k-1} \to j+2^k-1\) ,所以,两端的起点分别是 \(j\) 和 \(j+2^{k-1}\) 。基于此,我们就可以写出以下状态转移方程
现在我们也是成功的预处理出来了每一段长为 \(2^k\) 的区间的最大值,样例代码如下:
for (int i=1;i<=n;i++){
cin>>a[i];
dp1[i][0]=a[i];//注意要提前预处理
}
for (int i=1;(1<<i)<=n;i++){
for (int j=1;j+(1<<i)-1<=n;j++){
dp1[j][i]=max(dp1[j][i-1],dp1[j+(1<<(i-1))][i-1]);
}
}
这样的时间复杂度为 \(O(nlogn)\)
问题2——如何求解每个区间的极值
我们已经解决了预处理的问题了,现在我们就要去处理每个区间的问题了。这里我们就要用到前面所提到的一个定理,所有的实数都可以被写成若干个二进制相加。我们可以基于这个定理去求解每个区间的极值。
我们可以采取函数 \(log2\) 来求解当前这段所包含的最大的长度为 \(2^k\) 的 \(k\) ,然后从大到小依次枚举可行的指数 \(j(1\le j \le k)\) ,然后不断更新起点 \(x\) ,并且通过这个起点 \(x\) ,来确定当前是哪一段的答案,在根据可选的答案中选一个最大值。
样例代码如下:
cin>>x>>y;
int num=log2(y-x+1)+1;//多加一个,保险
for (int j=num;j>=0;j--){
if (x+(1<<j)-1<=y){
maxn=max(dp[x][j],maxn);
x+=(1<<j);//更新起点
}
}
cout<<maxn;
这样的时间复杂度是 \(O(logn)\)
除此之外,还有一个时间复杂度是 \(O(1)\) 的方法,但是在有些时候不能用,要小心加谨慎,高危 。
因为我们知道,我们求得是最大值,所以有重复也没有关系,那么一旦我们知道了当前区间的最大的 \(k\) ,那么我们是否也可以直接在前面找一个长度为 \(2^k\) 的区间,后面也找一个长度为 \(2^k\) 的区间就行了?只不过后面的区间的起点我们还要算一下罢了,这里就不算了,直接给出答案。
cin>>x>>y;
int num=log2(y-x+1);
maxn=max(dp[x][num],dp[y-(1<<num)+1][num]);
cout<<maxn;
但是这种方法只适用于求解可以重复的题目,如果当前题目要求的是传递到第几个人这种就不可以了。
例题
[USACO07JAN] Balanced Lineup G
题目描述
每天,农夫 John 的 \(n(1\le n\le 5\times 10^4)\) 头牛总是按同一序列排队。
有一天, John 决定让一些牛们玩一场飞盘比赛。他准备找一群在队列中位置连续的牛来进行比赛。但是为了避免水平悬殊,牛的身高不应该相差太大。John 准备了 \(q(1\le q\le 1.8\times10^5)\) 个可能的牛的选择和所有牛的身高 \(h_i(1\le h_i\le 10^6,1\le i\le n)\)。他想知道每一组里面最高和最低的牛的身高差。
输入格式
第一行两个数 \(n,q\)。
接下来 \(n\) 行,每行一个数 \(h_i\)。
再接下来 \(q\) 行,每行两个整数 \(a\) 和 \(b\),表示询问第 \(a\) 头牛到第 \(b\) 头牛里的最高和最低的牛的身高差。
输出格式
输出共 \(q\) 行,对于每一组询问,输出每一组中最高和最低的牛的身高差。
样例 #1
样例输入 #1
6 3
1
7
3
4
2
5
1 5
4 6
2 2
样例输出 #1
6
3
0
这道题就是典型的倍增的题目,只不过是要求一个最大值和一个最小值,可以用来练手。
#include<bits/stdc++.h>
using namespace std;
const int INF=5*1e5+10;
long long a[INF],dp1[INF][40],dp2[INF][40];
int main(){
int n,q;
cin>>n>>q;
for (int i=1;i<=n;i++){
cin>>a[i];
dp1[i][0]=a[i];
dp2[i][0]=a[i];
}
for (int i=1;(1<<i)<=n;i++){
for (int j=1;j+(1<<i)-1<=n;j++){
dp1[j][i]=max(dp1[j][i-1],dp1[j+(1<<(i-1))][i-1]);
dp2[j][i]=min(dp2[j][i-1],dp2[j+(1<<(i-1))][i-1]);
}
}
for (int i=1;i<=q;i++){
long long maxn=INT_MIN,minn=INT_MAX;
int x,y;
cin>>x>>y;
int num=log2(y-x+1);
maxn=max(dp1[x][num],dp1[y-(1<<num)+1][num]);
minn=min(dp2[x][num],dp2[y-(1<<num)+1][num]);
cout<<maxn-minn<<endl;
}
return 0;
}
Pass An Note
题目描述
有 \(n\) 个小朋友在传纸条,编号 \(1\) 至 \(n\)。编号为 \(i\) 的小朋友如果收到了纸条,会传给编号为 \(a_i\) 的小朋友。
现在有 \(m\) 组询问,每组询问会给出参数 \(p\) 和 \(q\),问从小朋友 \(p\) 开始,传 \(q\) 次纸条会传到哪个小朋友手里。请求出每组询问的答案。
输入格式
第一行输入两个正整数 \(n\) 和 \(m\),保证\(n≤3×10^5\) ,\(m≤3×10^5\)。
第二行输入 \(n\) 个正整数 \(a_i\) ,保证 \(1≤ai≤n\) 接下来 \(m\) 行,每行两个正整数 \(p\) 和 \(q\),保证 \(1≤p,q≤n\) 。
输出格式
输出 \(m\) 行,每行一个正整数,表示从 \(p\)传递 \(q\) 次纸条会到达的人。
样例输入
10 10
5 2 10 4 9 4 8 10 6 2
5 3
5 7
7 10
8 2
8 1
7 7
8 1
5 4
3 5
9 4
样例输出
4
4
2
2
10
2
10
4
2
4
这道题就不能使用上述的 \(O(1)\) 的方法了,所以我们还是老老实实的敲 \(O(logn)\) 的方法吧。
#include<bits/stdc++.h>
using namespace std;
const int INF=5*10e5;
int a[INF],dp[INF][20];//dp表示从x开始传,传2^i次
int main(){
int n,m;
cin>>n>>m;
for (int i=1;i<=n;i++){
scanf("%d",&a[i]);
dp[i][0]=a[i];
}
for (int i=1;(1<<i)<=n;i++){
for (int j=1;j<=n;j++){
dp[j][i]=dp[dp[j][i-1]][i-1];
}
}
while (m--){
int x,y,ans;
scanf("%d %d",&x,&y);
int num=log2(y)+1;
for (int i=num;i>=0;i--){
if ((1<<i)<=y){
ans=dp[x][i];
x=ans;
y-=(1<<i);
}
}
printf("%d\n",ans);
}
return 0;
}
树上倍增
现在我们把这种思想放到树上来试试。
引入
我们常常在信息学中考到一种题型,叫做树上路径问题。对于这种树上问题,考察的内容和序列问题类似,在线性结构中遇到的问题大多可以照搬到树上来求解。
在序列问题中,比较常见的是区间查询,同样,在树中,经常也会遇到区间问题。
我们可以类比一下,区间,由左右两个端点确定,对于树上的两个点,他们之间的简单路径是唯一的,就是说这条简单路径就是由左右两个端点确定的一个区间,线性的区间问题在树上就是转变成了树上路径问题。树上路径问题查询内容和序列问题差不多,比如两点的路径长度,树上两点之间路径的极值等。
由树上距离到树上倍增
现在给定一棵树,要求多次询问两个点之间的最短路径。
很容易想到暴力做法,对于每次的查询 \(u\rightarrow v\),以 \(u\) 点或者 \(v\) 点为根,遍历一遍树并同时记录节点深度,当找到另一个点时,这个点的深度就是 \(u\rightarrow v\) 的距离。每次查询的时间复杂度为 \(\cal{O(n)}\),总时间复杂度为 \(\cal O(n^2)\) ,效率太低,可以考虑一点小小的优化。
\(u\rightarrow v\) 的路径是确定的,我们可以从一个点出发,依次找到这个路径上的其他点,直到找到另一个端点为止,这样我们就只遍历了有效的点,效率得到了提升。关键是如何只遍历这条路径上的点呢?从一个点出发,到底是该往父亲几点走,还是往其某个兄弟节点走,或者往其某个儿子节点走呢?
在一棵树中,对于每一个节点,儿子节点可以有多个,但是父亲节点有且仅有一个,所以我们找下一个节点时一般都是通过儿子节点找父亲。
我们会发现,这两个点向上的路径有一个交点 \(x\) ,这个交点把这条路径分成了两部分 \(u\rightarrow x\),\(x\rightarrow v\)我们知道找到这个点 \(x\),就可以快速通过深度差算出路径之和,那么如何找到这个点 \(x\) 呢。
第一种做法是分别从 \(u\) 点和\(v\) 点开始往根节点标记,再从根节点往下遍历,找到最后一个同时被标记的点即为两条路径的交点 \(x\) 。但是这种做法仍然会遍历很多路径之外的点,那么是否有办法只遍历路径上的点呢?仔细观察就可以发现,深度相同的点,同时向上移动,那么就会同时跳到点 \(x\) 的位置,因为 \(x\) 距离深度相同的点的路径长度相同。对于深度不同的点,怎么跳呢?我们可以先让深度较深的点跳到和深度较浅的点相同深度,再两个点一起网上跳跃,当跳到同一个点时,这个点就是需要的点 \(x\) 。
前面的做法,最坏时间复杂度都是 \(\cal O(n^2)\),效率的瓶颈在找这个点 \(x\) 的时间上,这个点 \(x\) 我们一般称之为两点的最近公共祖先。如何快速找最近公共祖先呢?之前的做法是一步一步往上移动,但是这种移动方法太慢,我们可以考虑更快的移动方式,这就要用到我们之前学习的倍增算法。
记录出每一个点向上移动 \(2^k\) 到达的点,对于任意一个距离,它对应的二进制数中,出现1的位就是需要跳的时候,而这个过程就是树上倍增。
树上倍增的具体实现
其实树上倍增大致可以分为三个步骤。
- dfs 预处理倍增数组设 \(dp[x][i]\) 表示 \(x\) 点向上跳 \(2^i\) 到达的点,初始值 \(dp[x][0]\) 的值就为 \(x\) 的父亲节点的编号,在从根节点往下遍历的过程中,我们已经得到了该点上方所有点的倍增信息,可以得到状态转移方程:
for (int j = 1; (1 << j) <= deep[x] - 1; j++) {
dp[x][j] = dp[dp[x][j - 1]][j - 1];
}
- 调整两点深度对于深度不同的点,找最近公共祖先比较麻烦,所以我们先把两点的深度统一,即让深度较深的点跳到和深度较浅的点同一深度。具体跳跃方法可以参考差值的二进制数,比如 \((10110)_2\) ,就需要向上跳 \(2^1,2^2,2^4\)。换言之就是,找当前数值中最大的 \(2^k\) 的数,找到后再减去这个数,然后继续找。
if (deep[x] < deep[y]) swap(x, y);
int index = __lg(deep[x] - deep[y]);
for (int i = index; i >= 0; i--) {
if (deep[dp[x][i]] >= deep[y])x = dp[x][i];
if (deep[x] == deep[y])break;
}
- 找最近公共祖先对于深度相同的两点 \(u\) , \(v\) ,他们的最近公共祖先可能是任意一个点,那么如何跳跃呢?我们观察这个两个点的 \(dp\) 数组可以发现,在 \(i\) 比较大的时候, \(dp[u][i]=dp[v][i]\) ,说明此时已经跳到了最近公共祖先上方,我们需要找到 \(dp[u][i]!=dp[v][i]\)
由于我们也不知道i的具体值,所以只能一个一个尝试,当树的深度最大为 \(10^5\) 时,\(i\) 的最大值为17即可,\(i\) 的值和数据范围 有关,一般不会超过20,如果发现 \(dp[u][i]==dp[v][i]\),则不动,否则就同时跳到 \(dp[x][i]\) 这个点,由于一个数一定对应一个二进制数,所以最终一定会跳到最近公共祖先。
for (int j = 18; j >= 0; j--) {
if (dp[x][j] == dp[y][j]) continue;
x = dp[x][j], y = dp[y][j];
}
return dp[x][0];
Tips:
对于边权为1的树,找到两点的最近公共祖先后,通过两点的深度差相减就能得到答案。对于边权不为1的树,虽然也是通过深度差相减得到答案,但是要注意,如果 deep 数组中存储的是该点到根节点的距离,那么在树上倍增第二步操作中,把两个点移动到相同深度的操作就是错误的,这里的深度指的是离根节点经过的节点数量,不是离根节点的距离,所以对于有边权的树,我们需要重新开一个距离数组 dis ,而不能直接修改 deep 数组,这两个在该代码中的作用是不一样的。
小结
树上倍增经常用来求解需要找最近公共祖先的问题,同样,对于序列问题,很多时候还需要求极值,树上倍增也可以用来处理树上路径的极值。处理办法和倍增求区间极值有一点区别,因为对于树上的每一个点,有唯一的父亲节点,但是儿子节点有很多,没有办法记录祖先节点向下找 \(2^k\) 这个区间内的答案。
那么如何求解 \(u\) 点到最近公共祖先 \(x\) 之间的极值呢?先维护一个极值的倍增数组,\(max[x][i]\) 表示 \(x\) 点到 \(x\) 向上移动 \(2^i\) 这个区间的极值,在 \(u\) 点往上跳的过程中,同时更新极值即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号