P10432 [JOISC 2024] 滑雪 2 (Day1)

P10432 [JOISC 2024] 滑雪 2 (Day1)

题目描述

JOI 先生管理着 IOI 高原上一家著名的滑雪度假村，他决定为滑雪度假村开业 15 周年庆祝活动而在相邻的 KOI 高原上建造一家新的滑雪度假村。

KOI 高原有 \(N\) 个点，编号从 \(1\) 到 \(N\)。目前，第 \(i\) 个点（\(1 \leq i \leq N\)）的海拔高度为 \(H_i\) 米，并且高原上的每个点都没有连接起来的滑道。此外，每个点都配备了一个未使用的连接设施。

JOI 先生的目标是在高原上的一个点上建造 KOI 酒店，然后建造一些滑道连接高原上的每个点，以便人们可以从任何一个点滑雪到酒店。具体来说，JOI 先生将按照以下步骤建造滑雪度假村：

1. 进行以下筑堤工作任意次数（可能为零）：选择一个点 \(i\)，将点 \(i\) 的海拔高度增加 1 米。此工作的成本为每次操作 \(K\)。

2. 从 \(N\) 个点中选择一个点，并在那里建造 KOI 酒店。

3. 进行以下扩展工作任意次数（可能为零）：选择一个点 \(i\)，在点 \(i\) 建造一个连接设施。此工作的成本为每次操作 \(C_i\)。

4. 对于除了 KOI 酒店所在点之外的剩余 \(N - 1\) 个点，执行以下构建：设 \(i\) 为该点的编号。选择另一个海拔严格较低的点 \(j\)，并使用点 \(j\) 的一个未使用的连接设施，从点 \(i\) 向点 \(j\) 构建单向滑道。注意，如果没有海拔严格较低且有未使用连接设施的点 \(j\)，则无法实现目标。

滑雪度假村的建造成本是进行堤岸工作和扩展工作的成本之和。

编写一个程序，给定 KOI 高原上每个点的信息和每次筑堤工作的成本 \(K\)，找到建造滑雪度假村的最小成本。

输入格式

从标准输入中读取以下数据：

• \(N\) \(K\)
• \(H_1\) \(C_1\)
• \(H_2\) \(C_2\)
• ...
• \(H_N\) \(C_N\)

输出格式

输出一行，构建滑雪度假村的最小成本。

输入输出样例 #1

输入 #1

5 2
0 6
1 1
0 5
2 1
1 2

输出 #1

8

说明/提示

样例解释 1

例如，可以按以下方式建造滑雪度假村：

1. 在点 \(1\) 进行两次筑堤工作，在点 \(5\) 进行一次。这些筑堤工作的总成本为 \(2 \times (2 + 1) = 6\)。每个点的海拔高度变为 \(2, 1, 0, 2, 2\) 米。
2. 在点 \(3\) 建造 KOI 酒店。
3. 在点 \(2\) 进行两次扩展工作。这些扩展工作的总成本为 \(1 \times 2 = 2\)。结果，从点 \(1\) 开始，每个点的连接设施数量变为 \(1, 3, 1, 1, 1\)。
4. 构建 \(4\) 条滑道：一条从点 \(1\) 到点 \(2\)，一条从点 \(2\) 到点 \(3\)，一条从点 \(4\) 到点 \(2\)，一条从点 \(5\) 到点 \(2\)。

因此，构建滑雪度假村的成本为 \(6 + 2 = 8\)。由于无法以不超过 \(7\) 的成本建造滑雪度假村，因此输出 \(8\)。

此样例输入满足子任务 \(3,4,5,6\) 的约束条件。

约束条件

• \(1 \leq N \leq 300\)
• \(1 \leq K \leq 10^9\)
• \(0 \leq H_i \leq 10^9\)（\(1 \leq i \leq N\)）
• \(1 \leq C_i \leq 10^9\)（\(1 \leq i \leq N\)）
• 给定的值均为整数。

Solution:

性质题，所以我们来挖掘一些性质：

首先我们想象一下最终的滑雪度假村长什么样：

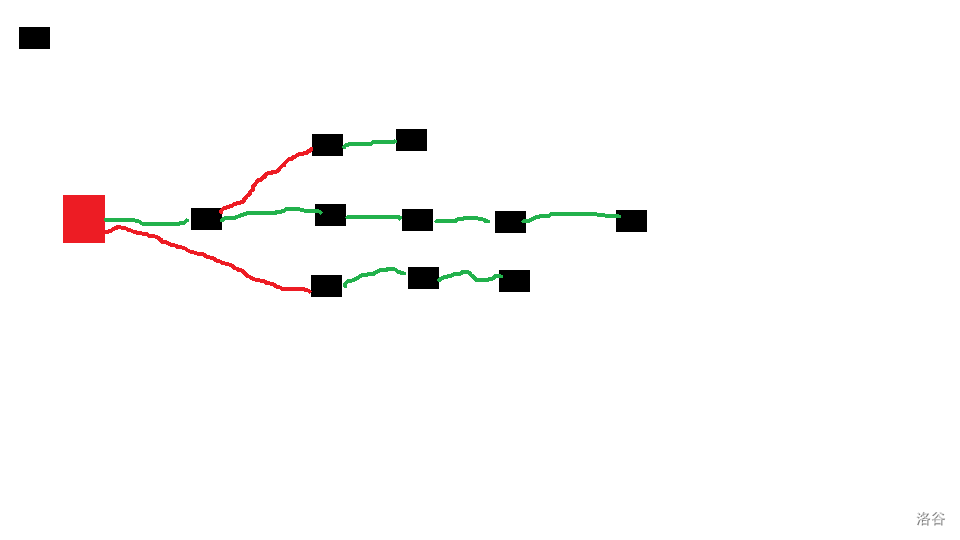
大概长这样，图中从左到右海拔严格递增，同一横坐标下的不同点表示海拔相同的不同点，图中绿色的边是免费的，红色的边是收费的，我们认为图中纯绿色边链接的最长的那条链叫做“主链”，剩下叫副链。在同一海拔下，我们将所有在原图上 \(C_i\) 值最小的点 \(i\) 放在主链上。

然后我们可以发现：

1.一个点不可能既升高海拔又新建装置。

• 因为我们升高一个点的目的就是将他并入完全不收费的主链上，而新建装置的目的是在主链中找一个点 \(i\) 来新建装置，以链接一条副链。乍一听没什么问题，可是如果一个点 \(i\) 不在主链上，然后他又升高海拔向右移动了，那么说明在 \(i\) 原来的位置上有一个 \(C\) 值比 \(i\) 更小的节点 \(j\) 可以用于当前节点的链接，即“只有原始主链上的点才会新建装置”。

2.存在一种最优策略，使得每一个高度上都至少有一个点不被抬高，且这个点一定是该高度上 \(C\) 最小的点

• 这是比较显然的，因为如果我们将一个海拔下的所有点全部抬高了，我们并没有将任何的点插入到主链中，而且还产生了很多额外花费。

到此，我们的性质已经足够我们进行一些简单的 \(dp\) 来思考这个问题了:记 \(dp_{i,j,k}\) 表示当前考虑海拔 \(i\) ，前面还有 \(j\) 个可供使用装置,当前海拔下有 \(k\) 个不在此海拔停留(既不在主链上，也不在此新建副链)的点时的最小花费。

• 首先有一种转移是将第三维合并，得到：
  \(dp_{i,j,k}+k\times K \rightarrow dp_{i+1,j,k+cnt_{i+1}}\)
  其意义是将仅升高 \(k\) 个点。

• 然后是枚举使用 \(x\le j\) 个先前的免费节点 :
  \(dp_{i,j,k} \rightarrow dp_{i+1,j,k-x+cnt_{i+1}}\)
  注意，因为使用一个先前的免费节点之后自己会成为一个新的免费节点，所以我们的第二维是无需更改的。

• 同时枚举在前面新增 \(y \le k+cnt_{i+1}-x\) 个收费装置并链接当前海拔的一个点：
  \(dp_{i,j,k} \rightarrow dp_{i+1,j+y,k-x-y+cnt_{i+1}}\)

复杂度分析：枚举海拔是 \(O(H)\) 的，然后状态转移中\(j,k,x,y\) 都是 \(O(N)\) 的，总复杂度来到了 \(O(H\times N^4)\) 十分难以接受。

然后我们仔细思考一下会发现，枚举 \(x,y\) 全都是无意义的：
使用一个先前的免费节点之后自己会成为一个新的免费节点
这句话告诉我们，只要先前有免费节点，如果当前点要新建一个链接，将它用掉一定是最优的,也就是说，如果我们在建立链接时，要么不连，要么就将当前状态 \(dp_{i,j,k}\) 下的 \(min(j,k)\) 全部连完。

这样我们就把枚举 \(x\) 优化掉了：

• 对于连接：
  \[dp_{i,j,k} +k\times K\rightarrow dp_{i+1,j,k-j+cnt_{i+1}} \ j\ < k+cnt_{i+1} \]
  \[dp_{i,j,k} +k\times K\rightarrow dp_{i+1,j,0} \ j\ge k+cnt_{i+1} \]

对于枚举 \(y\) 的优化：

• 我们直接在 \(i+1\) 内新增转移：

\[dp_{i+1,j,k-j+cnt_{i+1}} +C_{min}\rightarrow dp_{i+1,j+1,k-j-1+cnt_{i+1}} \ j < k+cnt_{i+1} \]

• 相当于将原来枚举 \(y\) 的进程转化成了随着枚举 \(k\) 进行的完全背包，正确性是显然的。

这样一来我们的时间复杂度就来到了 \(O(H\times N^2)\) ，接下来考虑离散化 \({H_i}\) :

虽然中间状态可能涉及 \(O(H)\) 种高度，但是最终答案中的高度只有 \(O(N)\) 种，所以我们思考到底哪些高度会出现在最终的最优解中:

还记得我们之前提过一个叫做“主链”的东西，主链上的点的高度就是全部的有效高度。那么我们考虑主链上会产生哪些高度：

"我们升高一个点的目的就是将他并入完全不收费的主链上"
“只有原始主链上的点才会新建装置”

假设我们手上现在有了一些不在原始主链上的点 \(x\) ，并且已经确定了他们在要在最终的答案中被塞入主链中,我们一定会选择主链上在 \(x\) 右边的第一个空位 \(pos\)

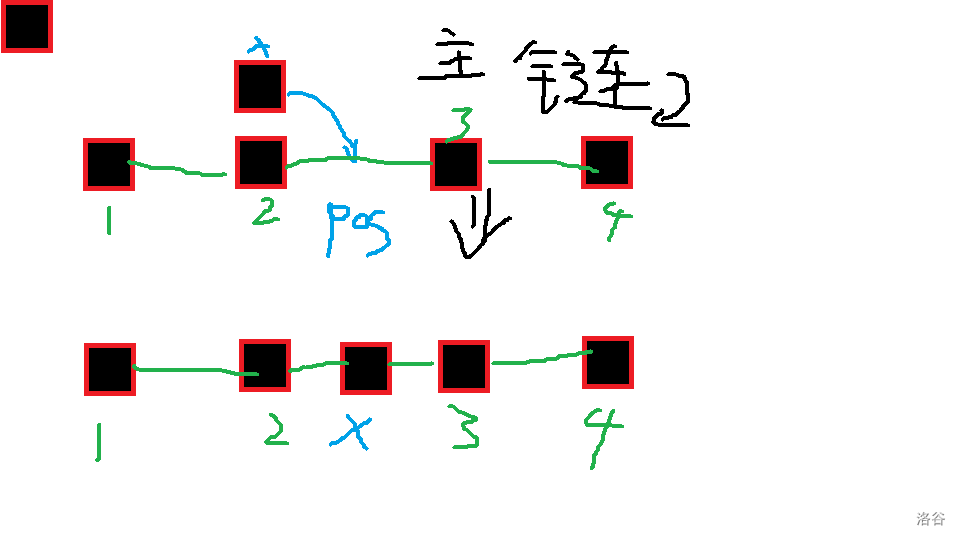
那么我们不难发现，在最终答案中可能的有效的高度实际上就是将所有不在主链上的点向右依次排开得到的高度集合 \(H_i'\)

这样我们就将时间复杂度降到了 \(O(N^3)\)，可以通过此题。

Code:

#include<bits/stdc++.h>
#define ll long long
#define int long long
#define rep(i,j,k) for(int i=j;i<=k;i++)
#define rrep(i,j,k) for(int i=j;i>=k;i--)
using namespace std;
const int N=305;
const ll inf=1e12;
const ll INF=1e18;
int n,cost;
int f[N][N][N],minc[N],sum[N];
int h[N],H[N],c[N],cnt[N];
int Max(int x,int y){return x>y ? x : y;}
int Min(int x,int y){return x<y ? x : y;}
void work()
{
    cin>>n>>cost;minc[0]=INF;
    rep(i,1,n){scanf("%lld%lld",&h[i],&c[i]);H[i]=++h[i];minc[i]=INF;}
    sort(H+1,H+1+n);
    rep(i,2,n)H[i]=Max(H[i],H[i-1]+1);
    rep(i,1,n){cnt[h[i]=lower_bound(H+1,H+1+n,h[i])-H]++;minc[h[i]]=Min(minc[h[i]],c[i]);}
    rep(i,1,n){minc[i]=Min(minc[i-1],minc[i]);sum[i]=sum[i-1]+cnt[i];}
    rep(i,0,N-1)rep(j,0,N-1)rep(k,0,N-1)f[i][j][k]=inf;
    f[1][1][cnt[1]-1]=0;
    rep(i,1,n-1)rep(j,0,n)rrep(k,Max(0ll,sum[i]-1),0)
    {
        int kk=k+cnt[i+1],w;
        if(k&&(H[i+1]-H[i])*cost>inf)w=inf+1;
        else {w=k*(H[i+1]-H[i])*cost;}
        if(kk<=j)f[i+1][j][0]=Min(f[i+1][j][0],f[i][j][k]+w);
        else
        {
            f[i+1][j][kk-j]=Min(f[i+1][j][kk-j],f[i][j][k]+w);
            f[i+1][j+1][kk-j-1]=Min(f[i+1][j+1][kk-j-1],f[i+1][j][kk-j]+minc[i]);
        }
    }
    int ans=INF;
    rep(j,0,n)ans=Min(ans,f[n][j][0]);
    printf("%lld",ans);

}
#undef int
int main()
{
    //freopen("P10432.in","r",stdin);
    //freopen("P10432.out","w",stdout);
    work();
    return 0;
}