P7302 [NOI1998] 免费的馅饼

P7302 [NOI1998] 免费的馅饼

题目描述

SERKOI 最新推出了一种叫做“免费馅饼”的游戏：游戏在一个舞台上进行。舞台的宽度为 \(w\) 格（从左到右依次用 \(1\) 到 \(w\) 编号），游戏者占一格。开始时游戏者可以站在舞台的任意位置，手里拿着一个托盘。下图为天幕的高度为 \(4\) 格时某一个时刻游戏者接馅饼的情景。

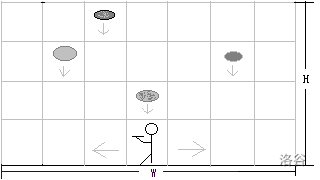
游戏开始后，从舞台天幕顶端的格子中不断出现馅饼并垂直下落。游戏者左右移动去接馅饼。游戏者每秒可以向左或向右移动一格或两格，也可以站在原地不动。

当馅饼在某一时刻恰好到达游戏者所在的格子中，游戏者就收集到了这块馅饼。当馅饼落在一个游戏者不在的格子里时该馅饼就消失。

写一个程序，帮助我们的游戏者收集馅饼，使得所收集馅饼的分数之和最大。

提示

对于 \(100\%\) 的数据，\(1 \leq w \leq 10^8\)，\(1 \leq n \leq 10^5\)，\(1\leq t_i \leq 10^8\)，\(1\leq p_i \leq w\)，\(1\leq v_i \leq 1000\)。

Solution:

有趣 dp 题。

首先我们不难想到拆绝对值:
令 \(t_{j} \le t_{i}\) 对于 \(i\) 所有合法的 \(j\) 应该满足：

\[ \left\{ \begin{aligned} p_{i}-p_{j} \le 2*(t_{i}-t{j})　p_{i} \ge p_{j} \\ p_{j}-p_{i} \le 2*(t_{i}-t{j})　p_{j} \ge p_{i} \end{aligned} \right. \]

然后我们整理一下：

\[ \left\{ \begin{aligned} p_{i}-2t_{i} \le p_{j}-2t_{j}　p_{i} \ge p_{j} \\ p_{j}+2t_{j} \le p_{i}+2t_{i}　p_{j} \ge p_{i} \end{aligned} \right. \]

$　　　　　\Longrightarrow $

\[ \left\{ \begin{aligned} 2t_{j}-p_{j} \le 2t_{i}-p_{i}　p_{i} \ge p_{j} \\ p_{j}+2t_{j} \le p_{i}+2t_{i}　p_{j} \ge p_{i} \end{aligned} \right. \]

$　　　　　\Longrightarrow $

\[ \left\{ \begin{aligned} 2t_{j}-p_{j} \le 2t_{i}-p_{i}　p_{i} \ge p_{j} \\ +　　　　　　　..\\ p_{j} \le p_{i}　　　　　 　.\\ \\ p_{j}+2t_{j} \le p_{i}+2t_{i}　p_{j} \ge p_{i}\\ +　　　　　　　..\\ -p_{j} \le -p_{i}　　　　 　..\\ \end{aligned} \right. \]

$　　　　　　　\Longrightarrow $

\[ \left\{ \begin{aligned} 2t_{j}\le 2t_{i}　p_{i} \ge p_{j} \\ 2t_{j} \le 2t_{i}　p_{j} \ge p_{i} \\ \end{aligned} \right. \]

$　　　　　　　　　\Longrightarrow $

\[ \left\{ \begin{aligned} t_{j}\le t_{i} \\ \end{aligned} \right. \]

也就是说，如果上述两种情况都被满足了，那么这个 \(j\) 就一定合法

即只要满足

\[ \left\{ \begin{aligned} 2t_{j}-p_{j} \le 2t_{i}-p_{i}　 \\ and　　　　　\\ p_{j}+2t_{j} \le p_{i}+2t_{i}　 \\ \end{aligned} \right. \]

然后怎么做？当然是线段树优化 dp 了，我们先对所有点以 \(2t_{i}-p_{i}\) 为关键字排序，然后开一颗线段树，在区间 \([1,2t_{i}+p_{i}]\) 上查询 \(f_{j}\) 的最大值。将当前答案 \(f_{i}=f_{j}+w_{i}\) 挂在线段树下标 \(2t_{i}+p_{i}\) 上。

然后这题就做完了

Code:

#include<bits/stdc++.h>
const int N=1e5+5;
const int inf=3e8;
using namespace std;
inline int Max(int x,int y){return x > y ? x : y;}
inline int Min(int x,int y){return x < y ? x : y;}
struct Node{
    int tim,dis,w;
    bool operator <(const Node &e)const{
        return 2*tim-dis < 2*e.tim-e.dis;
    }
}q[N];
int n,m,cnt;
struct Segment_Tree{
    int cnt,rt[N];
    struct Tree{
        int ls,rs,val;
    }t[N*32];
    void pushup(int x){t[x].val=Max(t[t[x].ls].val,t[t[x].rs].val);}
    void upd(int &x,int l,int r,int pos,int val)
    {
        if(!x)x=++cnt;
        if(l==r){t[x].val=Max(t[x].val,val);return;}
        int mid=l+r>>1;
        if(pos<=mid)upd(t[x].ls,l,mid,pos,val);
        if(mid<pos) upd(t[x].rs,mid+1,r,pos,val);
        pushup(x);
    }
    int query(int x,int l,int r,int L,int R)
    {
       if(L<=l&&r<=R){return t[x].val;}
       int mid=l+r>>1,res=0;
       if(L<=mid)res=Max(res,query(t[x].ls,l,mid,L,R));
       if(mid<R) res=Max(res,query(t[x].rs,mid+1,r,L,R));
       return res;
    }
    #undef ls
    #undef rs
}T;
int f[N];
void work()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&q[i].tim,&q[i].dis,&q[i].w);
    }
    sort(q+1,q+1+m);
    cnt=m;
    for(int i=1;i<m;i++)
    {
        if(q[i].dis==q[i+1].dis&&q[i].tim==q[i+1].tim)q[i+1].w+=q[i].w,q[i]={inf,inf,inf},cnt--;
    }
    sort(q+1,q+1+cnt);
    for(int i=1;i<=cnt;i++)
    {
        f[i]=q[i].w;

        f[i]=T.query(T.rt[0],-inf,inf,-inf,2*q[i].tim+q[i].dis)+q[i].w;
        T.upd(T.rt[0],-inf,inf,2*q[i].tim+q[i].dis,f[i]);
        //cout<<"pos:"<<2*q[i].tim-q[i].dis<<" "<<2*q[i].tim+q[i].dis<<"="<<f[i]<<"\n";
    }
    int ans=0;
    for(int i=1;i<=cnt;i++)ans=Max(ans,f[i]);
    printf("%d", ans);
}
int main()
{
    //freopen("P7302_3.in","r",stdin);freopen("P7302.out","w",stdout);
    work();
    return 0;
}