国庆 Day2 强基物理

前言：和暑假讲的有重合，上午主要是刚体转动力学、转动惯量、积分求解。那么就结合暑假的部分一起整理了。晚上等老师发了笔记再来更新。

讲了几乎一上午的积分。就当做是复习暑假自学的高数上了。

为什么老师还不发笔记。。。明天去问。

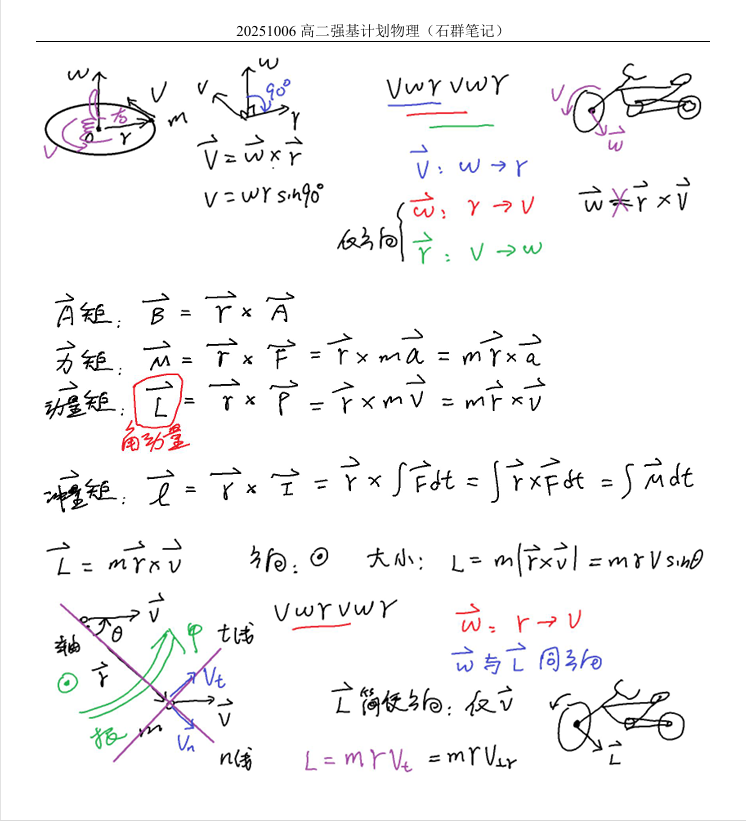
刚体转动力学核心就是两个新的关系：

角动量守恒 和 转动方程。

对应平动力学中的 能量守恒 和 加速度和力的关系。

或者角动量定理：冲量矩 = \(\Delta L\)。

而转动惯量 \(J\) 在公式表达中起到作用。注意对于质点的 \(J\) 就是 \(ml^2\)。

而转动惯量的研究很重要的一点就是各个模型对应的 \(J\) 的系数。直杆、圆盘、圆环、球体、球壳……转轴的不同也会影响。

另外就是平行轴定理：\(J_O=J_C+md^2\)，这意外着只需要知道质心轴的系数即可求解任何平行于质心轴的轴的系数。

垂直轴定理：设刚体所在平面为 \(Oxy\)，则 \(I_z=I_x+I_y\)。

在具体的分析问题中，通常分别考虑平动力学和转动力学各自列出方程，最后联立求解。

---

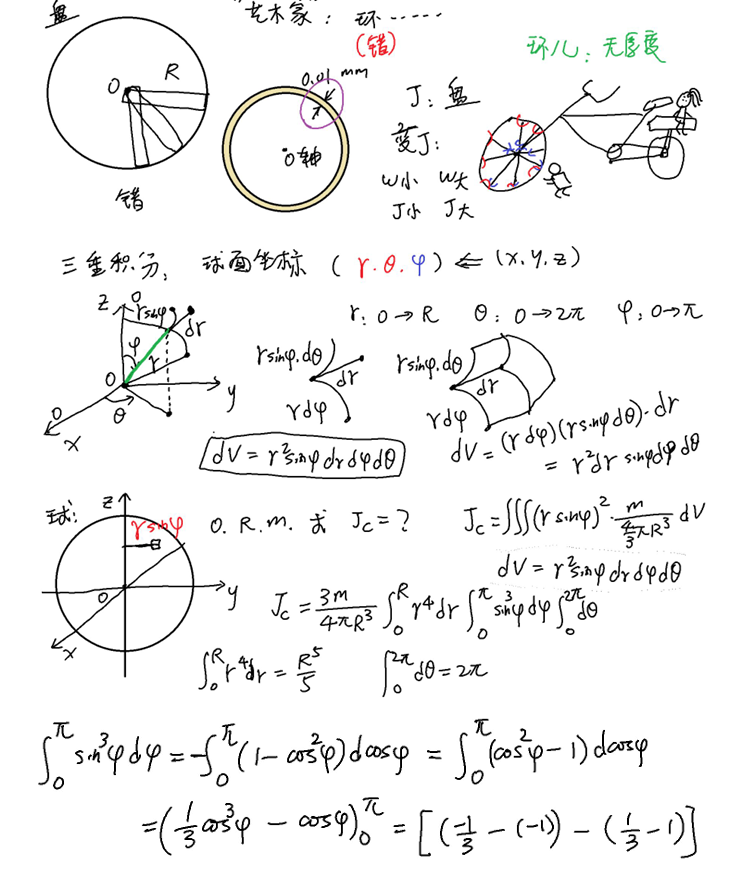
三重积分

如下图，三个变量 \(r,\theta,\alpha\)，表达出曲体的长宽高相乘，然后化简成各自的独立积分，乘起来即可。

注意 \(\sin^3\alpha\) 的积分，拆成 \((1-\cos^2\alpha)\sin\alpha\)，发现可以直接合并：\(\sin\alpha d\alpha=d\cos\alpha\)。

平动和转动各物理量关系

各个转动惯量

长杆绕中心：\(k=1/3\)。

长杆绕端点：\(k=1/12\)。

圆盘绕直径轴（二重积分）：\(k=1/4\)。

圆盘绕垂直轴：\(k=1/2\)。

圆环绕垂直轴：\(k=1\)。

圆环绕直径轴：\(k=1/2\)。

球：\(k=2/5\)。

球壳：\(k=2/3\)。

课堂笔记