数学拓展

T1 南开周考压轴

是否存在一个正方体，它的 8 个顶点到某一个平面的距离恰好为 \(0,1,2,3,4,5,6,7\)。给出其棱长。

题外话：做完这套卷子发现南开周考比八中难好多倍，倒数第二大题就卡了我好久……

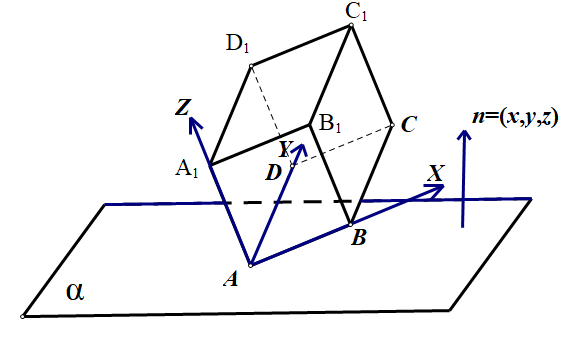
如果单纯建系暴算那么计算量无法承受。从点面距出发，引入平面法向量。

容易证明，只要如图示摆放，那么合法的构造一定是 \(A:0,B:1,C:2,D:3,A_1:4 ...\)。

发现只需要 AB,Ad,AA1 与 n 的数量积即可解出 \(a=\sqrt {21}\)。

再利用其余 4(3) 个点的信息，还可以求出这个平面的方程 \(4x+2y+z=0\)。

T2 *空间直线方程

• 可以用两平面相交线描述，即联立两平面方程。

Link：对于已知平面中的两个向量 \(m,n\)，可使用 \(s=m\times n\) 计算其法向量。

据此，将两平面法向量拿出来。易证得交线平行于两法向量。故容易计算出直线的方向向量。

• 参数方程。已知一点和单位向量。

• 点向式。\(\large \frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{t}\)。

T3 凑平方

已知向量 \(|a|=2,|b|=|c|=1\)，求 \((a-b)⋅ (c-b)\) min。

原式：\(a⋅c-a⋅b-b⋅c+1=\frac{1}{2}(a+c-b)^2-2\ge -2\)。当 \(b=a+c\) 取等。此时三向量平行。