双曲函数
0 引入
双曲函数经常出现在强基 / 高中数学最后一道大题中。其具有与三角函数相似的性质。值得探讨。
暂时地,只对正余弦和正切进行研究。后面如果探讨到与复数的联系,将会进一步拓展。
1 定义
\[\sinh x=\dfrac{e^x-e^{-x}}{2}
\]
\[\cosh x=\dfrac{e^x+e^{-x}}{2}
\]
\[\tanh x=\dfrac{e^x-e^{-x}}{e^x+e^{-x}}
\]
注意对于正切可以稍作处理:(同乘 \(e^x\) 得)
\[\tanh x=\dfrac{e^{2x}-1}{e^{2x}+1}=1-\dfrac{2}{e^{2x}+1}
\]
这样就可以很容易地分析函数最值等性质。
2 函数性质
2.1 基本探讨
正弦双曲函数与正弦函数一样是奇函数。其在 R 上单增。\(f(0)=0\)。
余弦双曲函数与余弦函数一样是偶函数。其在 \(x<0\) 单减,\(f(0)=1\),\(x>0\) 单增。
正切双曲函数与正切函数一样是奇函数。其在 R 上单增。\(f(0)=0\)。
2.2 进阶探讨
先看有点大的图:(蓝色为正弦 \(f(x)\),绿色为余弦 \(g(x)\),红色为正切 \(h(x)\))
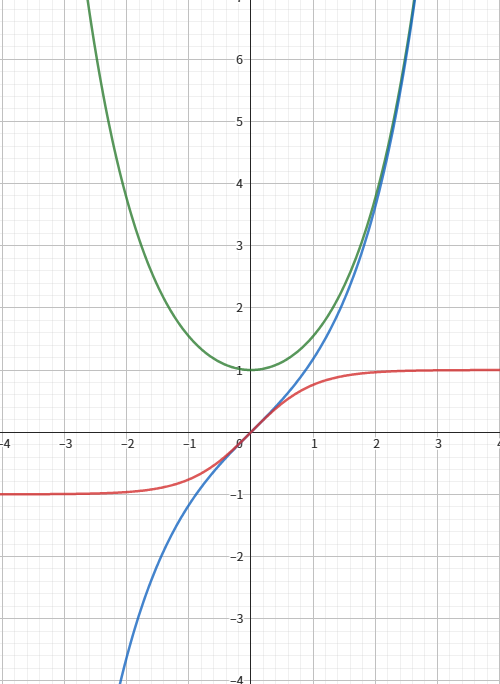
注意到正弦和余弦在 \(x>0\) 处随着 \(x\) 增大越来越近但是永不相交且永远 \(g(x)>f(x)\)。这是因为此时 \(f(x)-g(x)=e^{-x}\)。而 \(x\to +\infty,e^{-x}\to 0\)。
正弦和正切在 0 附近接近,但注意只在 \(x=0\) 处相交。\(x>0\) 时恒有 \(f(x)>h(x)\),\(x<0\) 时 \(f(x)<h(x)\)。
正切函数有渐进线 \(y=-1,y=1\)。这与 \(f,g\) 随 \(x\) 增大的接近有关。
3 恒等式
3.1 “随时准备着”
\[\cosh^2x-\sinh^2x=1
\]
证明容易。类比三角函数平方和为 1,双曲函数则是平方差为 1。
几何意义:\(P(\cos x,\sin x)\) 表示单位圆;而 \(P(\cosh x,\sinh x)\) 则表示双曲线。
3.2 和角公式
\[\sinh(x+y)=\sinh x\cosh y+\cosh x\sinh y
\]
\[\cosh(x+y)=\cosh x\cosh y+\sinh x\sinh y
\]
证明容易。类比三角函数:正弦相同,余弦的减变成加。正切也是相同。
3.3 二倍角
正弦和正切均相同。
而对于余弦双曲有:
\[\cosh 2x=2\cosh^2x-1=2\sinh^2x+1
\]
推导方法:连续使用 3.1 和 3.2 即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号