题解 【修墙】
【题目描述】
在地图上,土地可以大致用一个无限大的黑白二维矩阵表示,其中用户为白格,墙为黑格。由于墙很高,两个用户能够互相通信当且仅当在网格上这两个白格能够只经过四联通的白格相互到达。
经过一番细致的研究,发现这个地图可以由如下过程迭代构造。
地图上一开始只有一个白格。
一次迭代中,假设原来的地图为 \(A\),那么新的地图为
AA
AB
其中 \(B\) 为一个与 \(A\) 边长相同且全为黑格的正方形矩阵。
例如三次迭代之后,我们得到了这样一个矩阵(\(W\) 表示白格,\(B\) 表示黑格):

经过无限次迭代之后,我们就得到了土地对应的黑白矩阵。
无限大的地图,分析起来过于困难。每次会截出一个子矩阵,他想要知道这个子矩阵中的用户在墙的阻隔下组成了多少个联通块,联通块定义为极大的能够互相通信的用户集合。
由于一次询问不足以分析,需要进行 \(q\) 次询问。
【输入】
第一行一个正整数 \(q\)。
接下来 \(q\) 行每行四个正整数 \(x_1,y_1,x_2,y_2(1≤x_1≤x_2,1≤y_1≤y_2)\),表示询问以第 \(x_1\) 行第 \(y_1\) 列,第 \(x_2\) 行第 \(y_2\) 列为两对角的矩形内用户形成的联通块数。
【输出】
\(q\) 行,每行一个正整数,表示对应矩形内的联通块数量。
【输入样例】
4
1 1 5 5
2 2 3 6
4 2 7 5
2 2 2 2
【输出样例】
1
3
3
0
【提示】
【数据规模】
需要注意的是如果矩形内没有用户应该输出 \(0\)。
| 子任务编号 | 子任务分值 | \(q\) | \(x_2,y_2\) |
|---|---|---|---|
| \(1\) | \(20\) | \(≤300\) | \(≤300\) |
| \(2\) | \(20\) | \(≤3000\) | \(≤3000\) |
| \(3\) | \(30\) | \(≤100000\) | \(≤10^9\) |
| \(4\) | \(30\) | \(≤10^6\) | \(≤10^9\) |
良心数据人建议使用较快的输入输出方式。
好吧,只是因为我时间限制的范围看错了,但是用 fread 可以卡进 1s
【时间限制】
2000 ms
【内存限制】
1048576 KB
这题只要把证明出来结论,还是比较简单的。。吧
结论1:从0开始编号,对于第 \(i\) 行第 \(j\) 列,当 \((i\&j)=0\) 时当前块为白色,否则为黑色;
证明:
书:这是因为你每进行一次迭代,相等于添加一个新的二进制位,并把两维这位都为1的格子染黑
证毕
如果看的懂就不用看我的伪证了
伪证:
首先
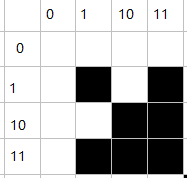
对于这个基本图形,结论是显然成立的
然后,合理外推
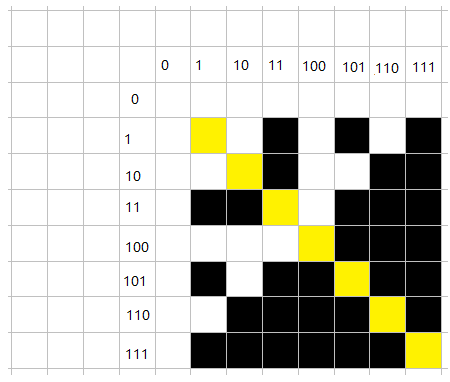
对于这些黄色的块
\(∵a\&a=a\)
\(∴\)它们是黑色的,符合题目的变化方法
那么我们继续考虑其他的块
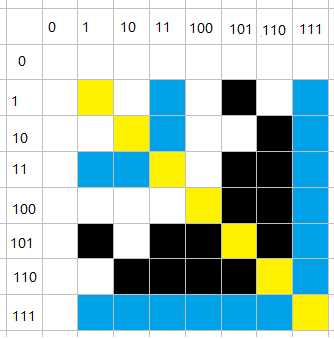
对于这些蓝色的块,它们的横纵坐标中有一个是 \((2^n+2^{n-1}+...+2^0)\) (即二进制下 \(n\) 个1)
所以对于块 \((x,y)\) 来说
只要 \(x\neq0\) 且 \(y\neq0\) 那么 \(x\&y\neq0\)
所以它们是黑色的,符合题意
然后
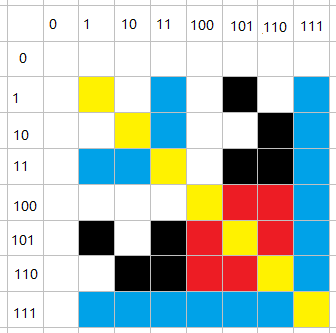
这些红色的块,我们假设有一个块 \(a\) 它的坐标为 \((x,y)\)
\(∵ x>\frac{n}{2}\) 且 \(y>\frac{n}{2}\)
\(∴\) x的二进制第一位和y的二进制第一位均为1
\(∴ x\&y\neq0\)
\(∴\) a 是黑的,符合题意
然后再考虑周期性
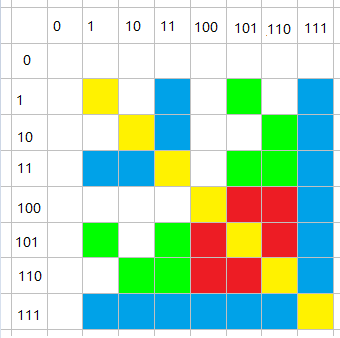
对于这些绿色的块来说
它们都可以由与它在同一行的一个黑色的点加上 \(2^n\) (即二进制前加个1) 变化而成
所以这些绿色的块也是黑的
然后合理外推,对于每个图形,该性质都是成立的
终上所述,当一个块 \((x,y)\) \(x\&y=0\) 时,它是白块,否则是黑块
伪证毕
结论2:对于每个子矩形
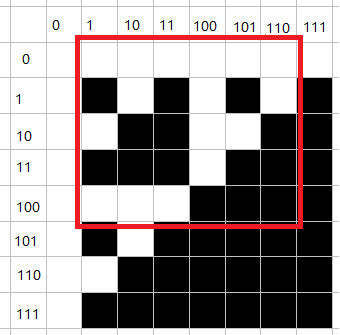
它的联通块的个数与一个L形内的联通块数量相同,如图
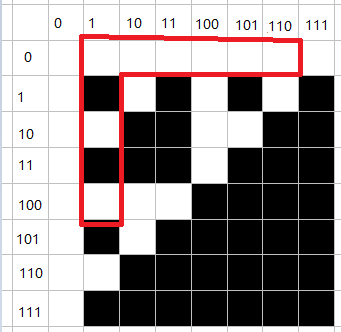
证明:

我们把所有的白色块连起来,可以看出无论你从哪个白色块出发都可以走到L上
并且白色块的连线构成了一棵树,所以在矩形的内部不会有连通块
证毕
由此,我们要求的矩阵的联通块数量就是L形中联通块的数量
我们只要算一维的情况就可以了
我们可以用前缀和来计算:\(联通块[l,r]=连通块[0,r]-联通块[0,l-1]+[l与l-1都为白色]\)
再特判一个 \(l=0\) 的情况就可以了
下面的内容比较玄学
我们看一个样例(二进制)
\(x=010,r=110\)
结合图可以看出,第 \(010\) 行的白色联通块的开头分别是
000 100
我们可以显然的看出,当 \(x\) 末尾有 \(n\) 个 \(0\) 时,\(r\) 末尾的 \(n\) 位对答案是没有影响的
所以我们可以将 \(x\) 和 \(r\) 同时右移 \(n\) 位
然后,我们从高位到低位扫描,当 \(r\) 与 \(x\) 的第 \(i+1\) 位都是 \(1\) 时,将 \(r\) 的最后 \(i\) 位全变为 \(1\)
因为当 \(r\) 与 \(x\) 的第 \(i+1\) 位都是 \(1\) 时,白色联通块的开头第 \(i+1\) 位绝对是 \(0\),所以即使 \(r\) 后 \(i\) 位每一位都为 \(1\),所得到的答案也不会大于 \(r\),所以可以将将 \(r\) 的最后 \(i\) 位全变为 \(1\)
然后我们考虑怎样求白色联通块的个数:
设 \(y\) 表第 \(x\) 行,\([0,r]\) 区间内白色连通块的起点,定义 \(sum=0\) 记录方案数
我们就枚举 \(x\) 的第 \(i+1\) 为 \(0\) 的情况,并使 \(sum=sum\times2+(bool)(r\&(1<<i))\)
下面我们详细介绍一下这个公式:
-
在 \(x\) 的第 \(i+1\) 为 \(1\) 的情况不更新 \(sum\),是因为当 \(x\) 这位为 \(1\) 时,\(y\) 这位只能取 \(0\),根据乘法原理 \(sum=sum\times1\) 相当于不变
-
在 \(r\) 第 \(i+1\) 位为 \(1\) 时,\(y\) 这一位既可以取 \(0\) 也可以取 \(1\),所以该位的贡献就是 \(2^i\) 所以 \(sum+1\)
最后返回前缀和时,返回 \(sum+1\),因为我们会漏掉空格全填 \(1\) 的情况
不难看出,第 \(x\) 行和第 \(x\) 列的块的颜色是一样的
所以,两个前缀和就好了。。。
标程(C++)
#include<bits/stdc++.h>
#define rint register int
using namespace std;
//省略输入输出优化
int sx,sy,ex,ey;
int ask(int x,int r){
if(r<0) return 0;
if(x==0) return 1;
while(x&&x%2==0) x/=2,r/=2;
for(rint i=29;i>=0;--i)
if((x&(1<<i))&&(r&(1<<i))){
r|=(1<<i)-1;
break;
}
int sum=0;
for(rint i=29;i>=0;--i)
if(!(x&(1<<i))) sum=(sum<<1)+(bool)(r&(1<<i));
return sum+1;
}
bool check(int x,int y){
if(x<0||y<0) return 0;
return (x&y)==0;
}
int main(){
int T; read(T);
while(T--){
read(sx); read(sy); read(ex); read(ey);
--sx; --sy; --ex; --ey;
int ans=ask(sx,ey)-ask(sx,sy-1)+(check(sx,sy-1)&&check(sx,sy))+ask(sy,ex)-ask(sy,sx-1)+(check(sx,sy)&&check(sx-1,sy))-check(sx,sy);
print(ans); putc('\n');
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号