【破环成链】【区间dp】LGP4342 [IOI1998]Polygon
【破环成链】【区间dp】LGP4342 [IOI1998]Polygon
题目可能有些许修改,但大意一致
多边形是一个玩家在一个有n个顶点的多边形上的游戏,如图所示,其中n=4。每个顶点用整数标记,每个边用符号+(加)或符号*(乘积)标记。
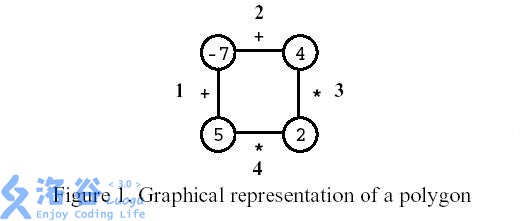
第一步,删除其中一条边。随后每一步:
选择一条边连接的两个顶点V1和V2,用边上的运算符计算V1和V2得到的结果来替换这两个顶点。
游戏结束时,只有一个顶点,没有多余的边。
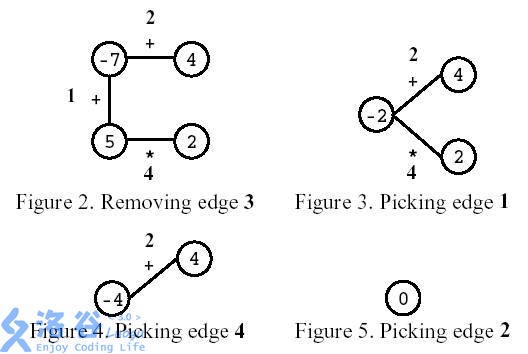
如图所示,玩家先移除编号为3的边。之后,玩家选择计算编号为1的边,然后计算编号为4的边,最后,计算编号为2的边。结果是0。
(翻译者友情提示:这里每条边的运算符旁边的数字为边的编号,不拿来计算)
编写一个程序,给定一个多边形,计算最高可能的分数。
输入格式
输入描述一个有n个顶点的多边形,它包含两行。第一行是数字n,为总边数。
第二行描述这个多边形,一共有2n个读入,每两个读入中第一个是字符,第二个是数字。
第一个字符为第一条边的计算符号(t代表相加,x代表相乘),第二个代表顶点上的数字。首尾相连。
3 < = n < = 50
对于任何一系列的操作,顶点数字都在[-32768,32767]的范围内。
输出格式
第一行,输出最高的分数。在第二行,它必须写出所有可能的被清除后的边仍能得到最高得分的列表,必须严格递增。
感谢@2016c01 提供的翻译
输入输出样例
输入 #1
4
t -7 t 4 x 2 x 5
很明显这里t表示这条边是加法边,然后后面那个数字表示这条边指向的结点的权值。
然后x代表乘法边。
输出 #1
33
1 2
题意
首先定义边的类型为加或者乘,然后每次可以选择一条边把两边的结点合并,合并运算就是结点内数字对应边的类型的运算。
比如说权值为1的点和权值为2的点通过加法边可以合并为\(1+2=3\)的一个点,继承原来点点所有边。
现在给出一个\(3\leq n\leq 50\)个点\(n\)条边的简单环,求进行\(n-1\)次操作后剩下那个点的点权最大值。
思路
进行\(n-1\)次操作,就相当于舍弃掉一条边,而剩下的边必须在区间上连续。
那么我们首先也是要破环成链,复制一份放在后面
然后又是合并问题了。
定义\(dp_{i,j}\)表示把区间\([i,j)\)的点合起来的最大权值,同样枚举中转点。
这里要慢一点,我们设边\(k\)的类型为\(\circ_k\),终点为第\(k\)个点
合并区间\([i,k)\)和区间\([k,j)\)用的就是\(\circ_k\)
然后合并的时候需要两边都有东西,所以\(k\in(i,j)\)
所以状态转移方程:
初始状态:\(dp_{i,i+1}=val_i\)
结束状态:因为是只进行了\(n-1\)次操作,但是合并了\(n\)个点,所以是\(\max_{0\leq i<n}\{dp_{1+i,n+i+1}\}\)
转移顺序:
- 区间长度升序\(len:[2,n]\)
- 区间起点升序\(i:[1,n-len+1]\),同时定义区间终点\(j=i+len\)
- 中转点升序\(k:(i,j)\)
注意到有负数所以\(dp\)数组其他元素初始值要是负数的极小值
打完回来
\(80pts\)
然后发现漏考虑了一些情况。
这里是有负数的。
是有负数乘法的。。。
负数乘以负数负负得正。
所以负数下乘数越小乘积越大。
所以我们不能只记录一个最大值,还需要记录一个最小值。
再分别讨论一下。
对于加法,肯定是小的加小的得到最小的,大的加大的得到最大的。
至于乘法,最小的可能是两个最小的相乘,也可能是最大的和最小的相乘,还可能是最大的和最小的相乘。。。
但是最大的就只有俩情况:最大和最大,最小和最小。
对于上述的五种情况,分别取个最值就可以维护最大值和最小值了
(真的有被坑到,不愧是IOI的题)
总结一下,整个题需要俩数组\(dp_{i,j}\)表示合成\([i,j)\)的最大值,\(mn_{i,j}\)表示最小值,然后有
答案就是\(\max_{0\leq i<n}\{dp_{1+i,1+n+i}\}\)
Code
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=128;
inline const int x(const int a,const int b)
{
return a*b;
}
inline const int t(const int a,const int b)
{
return a+b;
}
const int(*p[N])(const int,const int);
int val[N],dp[N][N],mn[N][N];
char tpe[N];
int nn,n,ans;
int main()
{
cin>>nn;
memset(dp,0x80,sizeof(dp));
memset(mn,0x01,sizeof(mn));
for(register int i=1;i<=nn;++i) cin>>tpe[i]>>val[i];
for(register int i=1;i<=nn;++i) tpe[i+nn]=tpe[i];
for(register int i=1;i<=nn;++i) val[i+nn]=val[i];
n=nn<<1;
for(register int i=1;i<=n;++i) p[i]=tpe[i]=='t'? t:x;
for(register int i=1;i<=n;++i) mn[i][i+1]=dp[i][i+1]=val[i];
for(register int len=2;len<=n;++len)
{
for(register int i=1;i<=n-len+1;++i)
{
const int j=i+len;
for(register int k=i+1;k<j;++k)
{
dp[i][j]=max(dp[i][j],(*p[k])(dp[i][k],dp[k][j]));
dp[i][j]=max(dp[i][j],(*p[k])(mn[i][k],mn[k][j]));
mn[i][j]=min(mn[i][j],(*p[k])(mn[i][k],mn[k][j]));
mn[i][j]=min(mn[i][j],(*p[k])(mn[i][k],dp[k][j]));
mn[i][j]=min(mn[i][j],(*p[k])(dp[i][k],mn[k][j]));
}
}
}
ans=dp[0][0];
for(register int i=0;i<nn;++i)
{
ans=max(ans,dp[1+i][nn+i+1]);
}
cout<<ans<<endl;
for(register int i=0;i<nn;++i)
{
if(ans==dp[1+i][nn+i+1])
{
printf("%d ",i+1);
}
}
printf("\n");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号