模拟赛C题的一种做法

注：这是本人的思路，当年代码丢了，我回头有空补一下

类似于题解，我们把所有数按 $\text{mod} $ \(c2\) 分类，类内从小到大排序，这样可知每个类内只有 \(\dfrac{n}{c2}\) 个数，因此考虑根号分治

1.当 \(c2\) 较小时，我们记 \(dp[n][S]\) 为\(n\) 个点，第 \(n\) 个点前 \(c2\) 个点的选择状态为 \(S\) ，转移就简单了

2.当 \(c2\) 较大时，\(\dfrac{n}{c2}\) 较小，即类内元素少，我们希望依类内元素状压，现在，我们把每个类按 \(c1\) 转移，发现如果把类 \(r\) 与 类 \((r+c1)\text{ mod } c2\) 连边，则一定会形成若干个环，环之间无关，直接考虑每个环

对于每个环，先断环成链，考虑链上一步的转移，看下图

现在，他就变成了一道裸的插头 dp,应当枚举下插头和有插头的状态转移

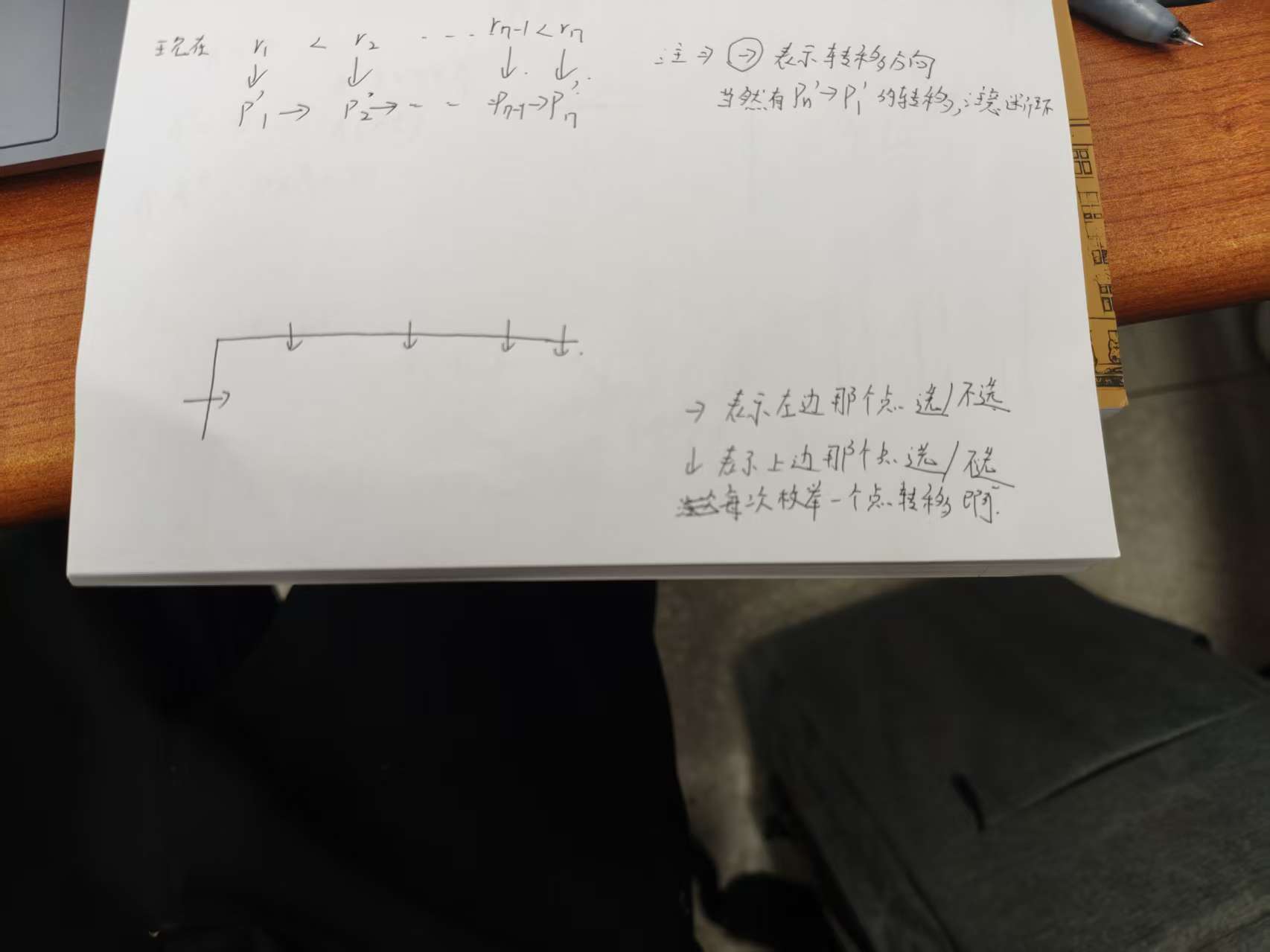
注意断环的情况与不断环的情况相比必须要求断环处必须匹配，不然会算重，实际上你也可以钦定环处是否转移然后 dp 两次