博弈论+杂题选讲
这里除了博弈论就是一些奇怪题
前置知识: nim 游戏和基础 SG 函数
阶梯博弈
差分一下,变为 阶梯 nim
阶梯nim是指,有 \(n\)堆石子,每次我们可以从第i堆的石子中拿走一部分放到第\(i-1\) 堆中,或者把第1堆中的石子拿走一部分
结论:阶梯nim的游戏结果与只看奇数堆的石子数的普通nim结果相同。
anti-SG
很简单,跟 nim 游戏的胜负条件相反,最后不能行动的人赢,我们称他为 anti-nim
这道题跟 nim 游戏相比,只有一处不同,要分情况
1.我们考虑每堆石子都只有一个,显然,奇数个先手输,偶数赢,此时 nim 和为 0
2.只存在一堆石子 >1 个,先手既可以通过拿完或只剩一个来任意创造 1 中所有情况,则必胜
3.多堆石子 >1 ,首先证明,在有限多步后,一定进入 2 情况,然后,2 情况异或和一定不为 0,
这与 nim 游戏的条件相同,类似的,套用 nim 的结论,nim 和不为 0 先手必胜,否则必败。
所以 在 nim 的基础上加一个特判即可。
类似的 anti-SG 游戏也存在 SG 函数,其与一般 SG 相同,除了获胜条件
对于Anti-SG游戏,如果我们规定当局面中所有单一游戏的SG值为0时,游戏结束,则先手必胜当且仅当
游戏的 SG 函数不为 0且游戏中某个单一游戏的 SG 函数值大于 1
游戏的 SG 函数为 0 且没有某个单一游戏的 SG 函数大于 1
muti-SG
我们在 nim 游戏上多了一种操作 将石子分成两个更小的堆(非0)
显然,有了 SG 函数以后这并不困难,相当于 SG[x],多了一种决策 SG[i] ^ SG[x-i].
在一般题这是足够的,但如果要解决 nim 是不够的
考虑 打表
点击查看代码
void init(){
sg[0] = 0,sg[1] = 1;
for(ll i = 2;i <= 505;i++){
memset(vis,false,sizeof vis);
for(ll j = 1;j <= i;j++) vis[sg[i-j]] = true;
for(ll j = 1;j < i;j++) vis[sg[j]^sg[i-j]] = true;
ll j = 0;
while(vis[j])sg[i] = ++j;
}
}
我们能得到如下结果
\( SG(x)=\left\{\begin{matrix}x-1,x\mod4 = 0 \\x,x\mod4=1~or~2 \\ x+1,x\mod4=3 \end{matrix}\right.\ \)
然后异或起来就可以了
将一个罐子看成一个状态十分困难,因为我们无法记录所有罐子。
转换思路,将每个石子看成一个状态,将一个石子移动到 n 记为一次有向图游戏
则我们只需关注每个罐子里石子的奇偶性即可(因为异或会抵消)
此时变为 muti-SG 游戏,且 n 极小,暴力求 SG 即可
every-SG
对于every-SG游戏有如下规则
对于还没有结束的单一游戏,游戏者必须对该游戏进行一步决策;
其他规则与普通SG游戏相同
理性分析一下
对于单个有向图游戏,如果必输,则输的一方会尽力缩短时间,相反,赢得一方会尽力延长时间
也就是说
对于SG值为0的点,我们需要知道最少需要多少步才能走到结束
对于SG值不为0的点,我们需要知道最多需要多少步结束
所以我们需要另一个变量 step 来记录
\(step_u=\max(step_v),SG_v\) 为 \(0\) 且 \(SG_u\) 不为 \(0\)
\(step_u=\min(step_v),SG_v\) 不为 \(0\) 且 \(SG_u\) 为 \(0\)
则对于Every-SG游戏先手必胜当且仅当单一游戏中最大的step为奇数
这个没啥题,了解一下
二分图博弈
二分图博弈是指,在一张二分图上,A可以在左部选择去到右部的哪一个节点,B可以在右部选择去到左部的哪一个节点。不可以重复经过一个节点。当无路可走时,在左部则B胜利,在右部则A胜利.保证起始点在左部,问谁获胜
结论:如果起始点 H 一定在最大二分图匹配中,则B必胜,反之,A胜利.
证明:
1.从左部的最大匹配点一定可以走到右部的最大匹配点
2.右部的最大匹配点只有无法行动和到左部的最大匹配点上。
我们对 2 进行反证法
假设走的路径是 \(H-P_1-P_2...P_k-T\)
其中 \(T\) 为 非匹配点
则有匹配 \(H-P_1,P_1-P_2...P_{k-1}-P_{k}\)
但也可以有
\(P_1-P_2...P_k-T\)的匹配
注意到 \(T\) 不是匹配点,即更换匹配之后最大匹配数不变,则 H 可以不是最大匹配,矛盾
故若 \(H\) 满足上述定义,则 B 一直往最大匹配上移动即可,B 必胜
假如 H 不一定是最大匹配点,因为后面这种匹配方式也是合法的。因为这两种匹配方式正好错位,所以换成这种匹配方式后,A,B 的处境互换,A 必胜
所以我们只需判断一个左部点是否一定是最大匹配点即可。
考虑如何判断
1.暴力删点,判断最大匹配是否减小
2.假如当前匹配点可以找到同侧的一个非匹配点,则当前点不必须
3.从非匹配点在交错树上搜索,搜到的匹配点都非必须
点击查看代码
void dfs2(int now)
{
ans[now]=1;
for(int i=head[now];i;i=e[i].next)
{
int v=e[i].to;
if(!vis[v])
{
vis[v]=1;
dfs(match(v));
}
}
}
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(dfs(i)) sum++;//这是匈牙利
else
{
memset(vis,0,sizeof(vis));
dfs(i);
}
}
树上删边
考虑 SG 函数
首先对于一个根节点来说,如果它有多个子节点,这相当于子游戏,由 SG 定理可知 根节点的 SG 值为以其为根的所有子树的 SG 值的异或和
现在考虑根节点只有一个孩子的游戏,也就是一条链的情况
数学归纳法可证 此时 SG 等于子节点的 SG+1
一些博弈论题
类 nim 游戏,关键是 SG 函数怎么设计
考虑路径是左上到右下的,我们需要设计一个 SG 函数,使得一次操作改且只改一次。
考虑右上到左下这条斜线,正好满足。
然后我们来用 nim 的思路找一下解
记录每条右上到左下这条斜线上所有数的异或和
考虑一次操作。
1.若开头斜线处的异或和不为零,则先手一定可以把它变成 0,同理异或和为零时,他所面临的永远为 0
2.改后面无意义,因为还可以改回来
3.终止时,当整个矩阵都是 0 时,异或和为 0,这个局面是后手必胜
综上所述,只有每一条从右上到左下的斜对角线异或和为 0 时,后手必胜
CF1149E
相似题,考虑相似的思路
问题还是在于状态的划分
一个先决条件是,在该 \(u\) 的同时 \(v\) 的状态不能与 \(u\) 相同,自然想到
\(mex\)
则我们记 \(val_u=mex\{val_v\}\)
类似的,我们尝试证明一下结论,即 \(S_p\) 为 \(val_u=p\) 的 \(h\) 的异或和,当且仅当 \(S_p\) 都为 \(0\) 后手获胜
类似的 上题 1,2,3 结论都成立,故可以证明
我们来考虑 A 的选择
1.取 RB/BR
2.取 RW/WR
A 肯定优先考虑操作一,B 同理
注意到 1 选择 RB颜色差不变,而 2 选择 显然是 RB 谁多谁赢,所以说如果最开始 RB 数量不同,则直接判断,谁多谁赢
现在考虑 RB 数量相同,只考虑 1 操作,由于其只发生在异色段中,我们单独考虑每一段形如 RBRB...的异色段即可
考虑求其 SG 函数
先考虑暴力求。
本题似乎不好优化 SG 的求值,考虑打表找规律
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int SG[20010];
int dfs(int now)
{
if(now==0||now==1) return 0;
if(now==2) return 1;
if(SG[now]!=-1) return SG[now];
int vis[20];
memset(vis,0,sizeof(vis));
for(int i=1;i<now;i++)
{
vis[dfs(i-1)^dfs(now-i-1)]=1;
}
SG[now]=0;
while(vis[SG[now]]) SG[now]++;
return SG[now];
}
int main()
{
freopen("txt.out","w",stdout);
memset(SG,-1,sizeof(SG));
for(int i=1;i<=200;i++)
{
if(SG[i]==-1) cout<<dfs(i)<<" ";
}
return 0;
}
于是我们得到了这个
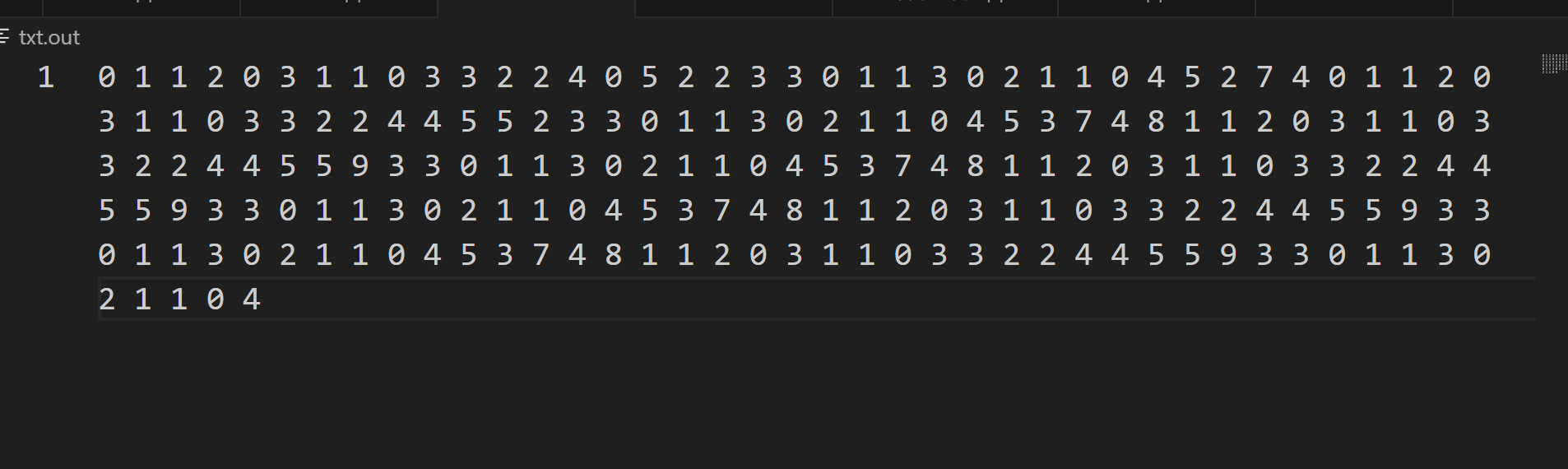
容易发现一个规律,似乎有循环节,但是前面没有。
那就特判,解决
``
点击查看代码
int rp[2001]={4,8,1,1,2,0,3,1,1,0,3,3,2,2,4,4,5,5,9,3,3,0,1,1,3,0,2,1,1,0,4,5,3,7};
int SG[2001];
int get_SG(int now)
{
if(now==0||now==1||now==15||now==35) return 0;
if(now==17||now==18||now==32||now==52) return 2;
return rp[now%34];
}
然后就做完了
OK 博弈论结束了,接下来的题就都不是人了(
一些 dp
套路(娃)题,你需要对各种 dp 优化十分熟悉,然后就是板子
暴力 \(dp\) 就不说了
大胆猜测这个转移是凸的,先来一个 wqs 二分
这时候问题就来了之后转移是 \(n^2\) 的
注意到括号序列满足四边形不等式,所以具有决策单调性,直接决策单调性分治
注意到这是在线的,用 cdq 变成离线就好了
是不是很简单
注意括号的贡献计算方式可用类似莫队的指针维护
本题还有个在广义笛卡尔树上斜率优化的 \(nlogn\) 算法,可以自行学习(因为我不会)
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
char c[200100];
int sta[200100],top;
int match[200100];
int pl[200100],pr[200100];
int cl,cr,sum,n;
int cnt[200100],id[200100],t;
int inf=1ll<<60,K,k;
int query(int l,int r)
{
while(l<cl)
{
cl--;
if(c[cl]=='('&&match[cl]<=cr) cnt[id[cl]]++,sum+=cnt[id[cl]];
}
while(cr<r)
{
cr++;
if(c[cr]==')'&&match[cr]>=cl) cnt[id[match[cr]]]++,sum+=cnt[id[match[cr]]];
}
while(cl<l)
{
if(c[cl]=='('&&match[cl]<=cr) sum-=cnt[id[cl]],cnt[id[cl]]--;
cl++;
}
while(r<cr)
{
if(c[cr]==')'&&match[cr]>=cl) sum-=cnt[id[match[cr]]],cnt[id[match[cr]]]--;
cr--;
}
return sum;
}
pair<int,int>f[200100];
void check(int l,int r,int ql,int qr)
{
if(l>r) return ;
int mid=(l+r)>>1;
pair<int,int>t=f[ql];
t.first+=query(ql+1,mid)+K;t.second++;
int pos=ql;
for(int i=ql+1;i<=qr;i++)
{
pair<int,int>p=f[i];
p.first+=query(i+1,mid)+K,p.second++;
if(p<t) t=p,pos=i;
}
f[mid]=min(f[mid],t);
check(l,mid-1,ql,pos);
check(mid+1,r,pos,qr);
}
void cdq(int l,int r)
{
if(l==0&&r==n)
{
for(int i=1;i<=n;i++) f[i]={inf,inf};
}
if(l==r) return ;
int mid=(l+r)>>1;
cdq(l,mid);check(mid+1,r,l,mid);cdq(mid+1,r);
}
signed main()
{
cin>>n>>k;
cin>>(c+1);
for(int i=1;i<=n;i++)
{
if(c[i]=='(') sta[++top]=i;
else if(c[i]==')')
{
if(top)
{
int x=sta[top];top--;
match[i]=x;match[x]=i;
}
}
}
while(top) match[sta[top--]]=n+1;
for(int i=1;i<=n;i++)
{
if(c[i]=='('&&!id[i])
{
t++;
for(int j=i;match[j]&&c[j]=='(';j=match[j]+1) id[j]=t;
}
}
cl=1;cr=0;
int l=0,r=1e10;
while(l<r)
{
int mid=(l+r)>>1;
K=mid;
cdq(0,n);
if(f[n].second>k) l=mid+1;
else r=mid;
}
K=l;
cdq(0,n);
cout<<(f[n].first-k*K)<<endl;
return 0;
}
给你 \(n\) 个区间 \([l_i,r_i]\) 和 \(m\) 个区间 \([l_i',r_i']\)
请对于 每一个 \(i,j\) 对求出有多少个\(a_1..a_i,b_1...b_j\) 使 \(\sum_{p=1}^i a_p=\sum_{q=1}^j b_q,l_p\leq a_p\leq r_p,l_p'\leq b_p\leq r_p'\)
\(n,m,l,r\leq 500\)
部分分 保证 \(\sum_{i=1}^n r_i\leq 500\) 且\(\sum_{i=1}^m r_i'\leq 500\)
sol
先考虑部分分 我们令 \(dp_{i,j,V}\) 表示 a ,b 序列分别到了 \(i,j\) 位置,且 \(\sum a_i-\sum b_j=V\) 的方案数
前缀和优化转移即可
考虑值域变大的情况
首先在部分分转移过程中,会有一个问题 \(dp_{i,j}\) 既可以从 \(dp_{i-1,j}\) 转移,又可以从 \(dp_{i,j-1}\) 转移,而且我们只需一次转移。
也许我们可以通过决定转移顺序来缩小值域,便有了如下做法
如果 \(V>0\) 从 \(dp_{i,j-1}\) 转移 使 \(V\) 减小,反之,从 \(dp_{i-1,j}\) 转移 使 \(V\) 增大
于是就可以了
点击查看代码
#include<bits/stdc++.h>
using namespace std;
struct IO{
int rd()
{
int x=0,w=1;
char c=getchar();
while(c<'0'||c>'9')
{
if(c=='-') w=-1;
c=getchar();
}
while(c>='0'&&c<='9')
{
x=(x<<3)+(x<<1)+c-'0';
c=getchar();
}
return x*w;
}
void write(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
void wt(int x,char c){write(x);putchar(c);}
}io;
const int N=500,V=1000;
int dp[N+50][N+50][V+50];
int n,m;
int la[N+50],ra[N+50],lb[N+50],rb[N+50];
const int mod=998244353;
signed main()
{
// freopen("txt.in","r",stdin);
// freopen("txt.out","w",stdout);
// cin>>n;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>la[i]>>ra[i];
for(int i=1;i<=m;i++) cin>>lb[i]>>rb[i];
dp[0][0][N]=1;
for(int i=0;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
if(i!=0||j!=0)
{
for(int k=1;k<=V;k++) dp[i][j][k]=(dp[i][j][k]+dp[i][j][k-1])%mod;
}
if(i<n)
{
for(int k=0;k<=N;k++)
{
dp[i+1][j][k+la[i+1]]=(dp[i+1][j][k+la[i+1]]+dp[i][j][k])%mod;
dp[i+1][j][k+ra[i+1]+1]=(dp[i+1][j][k+ra[i+1]+1]+mod-dp[i][j][k])%mod;
}
}
if(j<m)
{
for(int k=N+1;k<=V;k++)
{
dp[i][j+1][k-rb[j+1]]=(dp[i][j+1][k-rb[j+1]]+dp[i][j][k])%mod;
dp[i][j+1][k-lb[j+1]+1]=(dp[i][j+1][k-lb[j+1]+1]+mod-dp[i][j][k])%mod;
}
}
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cout<<dp[i][j][N]<<" ";
}
cout<<endl;
}
// fclose(stdin);fclose(stdout);
return 0;
}
给定 \(n\) ,求满足父亲编号小于儿子编号,儿子按编号顺序排列的树,其可能的 dfs 序种类数
其中 \(n\leq800\)
sol
首先,直接数 \(dfs\) 序显然不行,我们需要考虑 dfs 序是否合法,即由 dfs 序 能否还原出一棵树
我们尝试贪心的构造一棵树,首先先连一条链,此时 dfs 序 必定是递增的。
在面对下一个非递增树时,考虑再开一颗子树,此时挂的点只需要比他的兄弟编号大即可。
贪心的,点的位置越深越好(因为挂的深不会带来新的影响),所以我们挂在这样一个最深位置
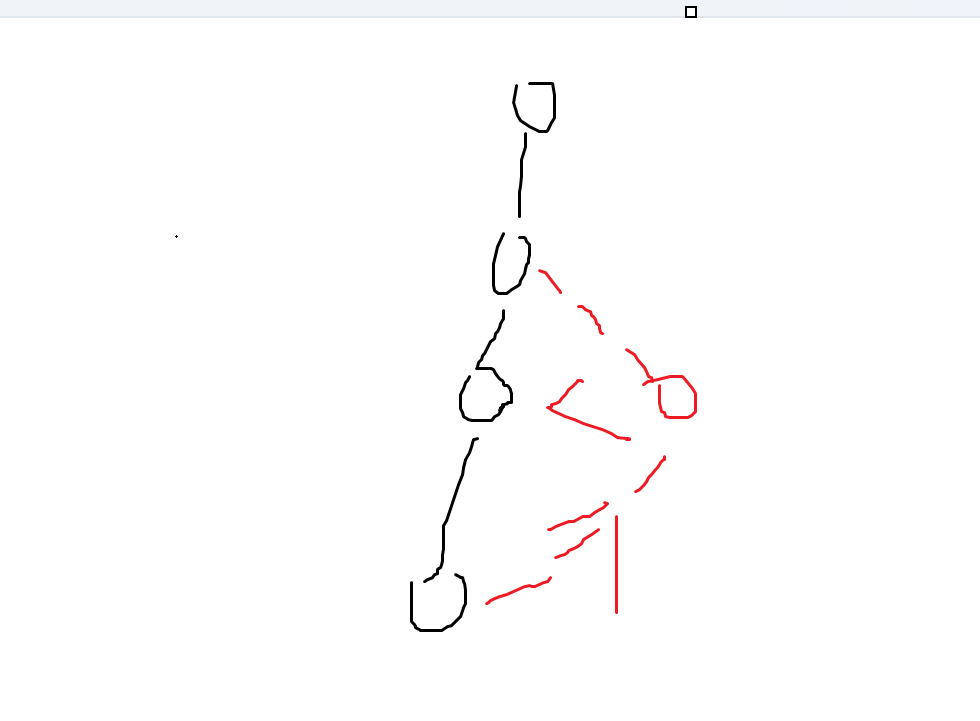
以此类推,我们就可以还原出一棵树
于是我们建立了一个dfs序到一棵树的双射
现在考虑计数,统计 dfs 序是不可能的,考虑统计树的个数
于是我们要统计这样的树的个数
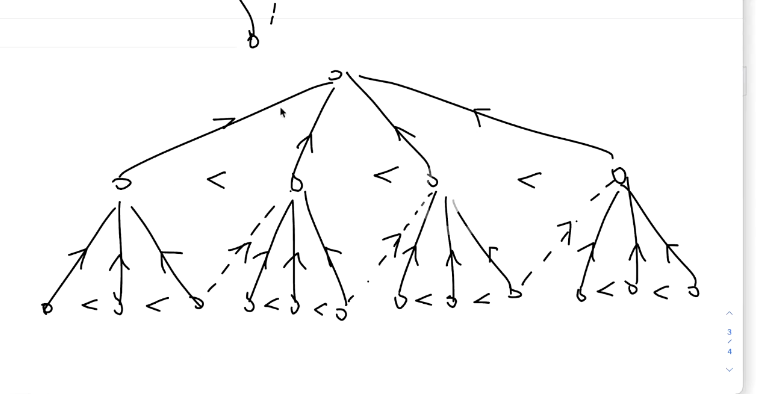
现在关系极多,考虑能否省去一些,发现可以,如下图

然后考虑计数
首先考虑一个模型,给定树的形态,要求父亲编号小于儿子,问标号方案数,结论是 \(n!\prod{1/size_i}\)
考虑套用,但原图连树都不是,考虑容斥即 $(u>v)= 无限制 - (u<v) $
注意到无限制显然是一棵树,而有限制时又有无用边,如下
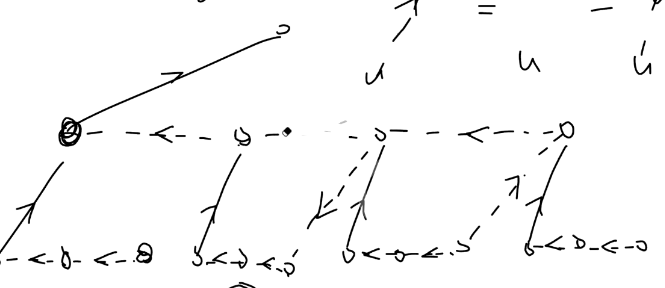
所以都成了树。
现在考虑 dp 所有 \(\prod 1/siz_i\),应按照经典模型,从叶子到根 dp
最后一步从儿子到父亲是容易的,考虑兄弟之间的 dp
记 \(d_{i,siz}\) 表示 dp 到了第 i 个点,目前 考虑了 \(siz\) 个节点的 所有 \(\prod 1/siz_i\) 和
考虑转移,先处理无限制的情况,只需枚举下一个点挂了多少节点即可,发现还得 dp
在令 f_i 表示上述状态,可以转移
现在考虑第二种的,发现难以转移,因为我们无法区分两种的区别
所以我们需要重新定义 dp 数组,发现两种的区别是 第二种会多一条上行边
于是定义 \(dp_{i,j}\) 表示考虑了 \(i\) 个点 目前希望之后走 j 条上行边 的所有树形态的\(\prod 1/siz_i\) 和,其中 \(f_i\) 可用 \(dp_{i,0}\) 表示 则有转移
\(dp[i][j]=(dp[i][j]+dp[i-1][j+1]+dp[i-k][j]*dp[k-1][0]-dp[i-k][j-1]*dp[k-1][0])*inv[i]\)
于是结束,但仍有一些边界问题,在代码中说明
点击查看代码
cin>>n>>mod;
if(n==1){puts("1");return 0;}//n=1 特判
inv[1]=1;
for(int i=2;i<=n;i++) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
dp[1][0]=1;//初始化
for(int i=2;i<=n;i++)
{
for(int j=0;j<=i;j++)
{
dp[i][j]=(dp[i][j]+dp[i-1][j+1])%mod;//儿子到父亲,一条上行边
if(j==0) dp[i][0]=(dp[i][0]+dp[i-1][0])%mod;//不走上行边了
for(int k=0;k<=i-j;k++)
{
dp[i][j]=(dp[i][j]+(dp[i-k][j]*dp[k-1][0]%mod))%mod;//容斥1
if(j) dp[i][j]=(dp[i][j]-1ll*(dp[i-k][j-1]*(dp[k-1][0]+(k==1)))%mod)%mod;//容斥2
}
dp[i][j]=dp[i][j]*inv[i]%mod;
}
}
int ans=dp[n-1][0]*inv[n];//根节点不能平行延伸,注意
for(int i=1;i<=n;i++) ans=ans*i%mod
不是 dp
有一个叫 减半报警器的 trick
首先注意到 x 最多有 6 个质因子,即一个监视器最多监视 6 个房子,则修改是好修改的。
现在考虑一个性质
\(\sum_{1\leq i\leq k}a_i=y\),则必有一个 \(a_i>(y/k)\)
因此我们可以当满足上述条件时再检查
检查之后,我们可以更新限制为\(\sum_{1\leq i\leq k}a_i=y -\sum_{1\leq i\leq k}a_i\),表示从这次检查开始之后的限制
注意到如果满足上述限制后 每次修改 \(y\) 至少变成原来的 \((k-1)/k\) 倍,所以至多 \(log_{(k-1)/k} y\) 次修改
考虑代码
我们对每个位置开一个优先队列来存 这个位置所有的报警器,每次去最小的看是否触发,如果触发就暴力修改当前监视器
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define pr pair<int,int>
using namespace std;
int n,m;
int sum[200100];
priority_queue<pr,vector<pr >,greater<pr > >q[200100];
vector<int>ans;
vector<int>val;
vector<vector<pr > >h;
vector<pr >H;
int prime[200100],cnt;
int mn[200100];
bool ringing[200100],vis[200100];
const int N=1e5+50;
void get_prime()
{
for(int i=1;i<=N;i++) mn[i]=i;
for(int i=2;i<=N;i++)
{
if(!vis[i])
{
prime[++cnt]=i;
}
for(int j=1;j<=cnt&&i*prime[j]<=N;j++)
{
vis[i*prime[j]]=1;
mn[i*prime[j]]=min(mn[i*prime[j]],prime[j]);
if(i%prime[j]==0) break;
}
}
}
void Ring(int x)
{
for(int i=0;i<h[x].size();i++)
{
pr now=h[x][i];
val[x]-=sum[now.second]-now.first;
h[x][i].first=sum[now.second];
}
if(val[x]<=0)
{
ringing[x]=1;
ans.push_back(x+1);
}
int tmp=(val[x]+h[x].size()-1)/h[x].size();
for(int i=0;i<h[x].size();i++)
{
pr now=h[x][i];
q[now.second].push({tmp+sum[now.second],x});
}
}
void add(int x,int k)
{
sum[x]+=k;
while(!q[x].empty())
{
pr now=q[x].top();
if(now.first<=sum[x])
{
q[x].pop();
if(!ringing[now.second]) Ring(now.second);
}
else break;
}
}
int las;
signed main()
{
cin>>n>>m;get_prime();
for(int i=1;i<=m;i++)
{
int op,x,y;
cin>>op>>x>>y;y^=las;
if(op==0)
{
while(x!=1)
{
int tmp=mn[x];
add(mn[x],y);
while(mn[x]==tmp) x/=tmp;
}
cout<<(las=ans.size())<<" ";
sort(ans.begin(),ans.end());
for(int j=0;j<ans.size();j++) cout<<ans[j]<<" ";
cout<<endl;
ans.clear();
}
else
{
H.clear();
while(x!=1)
{
int tmp=mn[x];
H.push_back({sum[mn[x]],mn[x]});
while(mn[x]==tmp) x/=tmp;
}
val.push_back(y);
h.push_back(H);
Ring(h.size()-1);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号