7.13 考试题

T1

这是原题

首先我们二分，转为判定性问题

考虑如何判定

显然，为了让上课时间最少，我们优先进行理解程度增加最多的课程

这样我们就能算出每个课程至少花多少时间

我们再将余下的天数用来补充那些超过规定时长的课程

最后看一下能不能将所有的课程都按时学完即可

点击查看代码

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

ll a[300100],b[300100];
ll n,m;

bool check(ll x)
{
    ll sum=0;
    for(int i=1; i<=n; i++)
    {
        if(a[i]>=b[i])
        {
            ll t=(x+a[i]-1)/a[i];//这是 x/a[i] 上取整，为至少天数
            if(t<=m) sum+=t;//若本身足够，不需补充天数,直接计入总天数
            else sum+=m+(x-a[i]*m+b[i]-1)/b[i];//需补充天数，计入
        }
        else
        sum+=(x+b[i]-1)/b[i];
        if(sum>n*m) return 0;
    }
    return sum<=n*m;//总天数<=n*m 即可
}
ll erfen(ll l, ll r)//二分
{
    while(l<r)
    {
        ll mid=(l+r)>>1;
        if(check(mid+1))
        l=mid+1;
        else
        r=mid;
    }
    return l;
}
int main()
{
    freopen("sixty.in", "r", stdin);
    freopen("sixty.out", "w", stdout);
    cin>>n>>m;
    for(int i=1; i<=n; i++)
    scanf("%lld", &a[i]);
    for(int i=1; i<=n; i++)
    scanf("%lld", &b[i]);

    cout<<erfen(0, 1e18);
    fclose(stdin); fclose(stdout);
    return 0;
}

T2

这是原题

找规律

对于一个成 \(S\) 型分布的座位 从左到右+从右到左 为一个循环，一共10个数

既然十个数一个循环，我们不妨看一下%10的余数

可以发现如下结论（借用一下题解图）

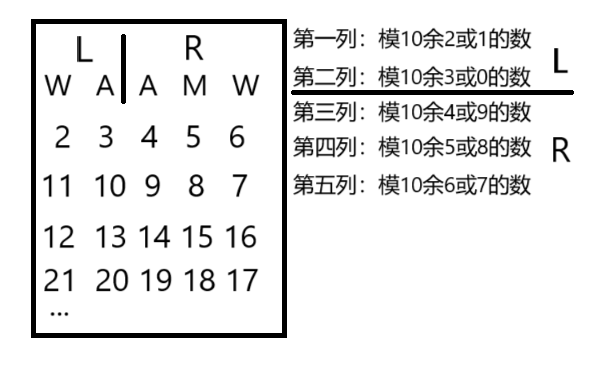
行号是好算的，不提

代码不放了，可以看原题题解

T3

由于 小熊的果篮 这个题本身就可以扩展颜色，所以原题做法可以直接移植

直接看代码即可

点击查看代码

#include<bits/stdc++.h>
using namespace std;

struct node
{
    int pos,cnt,col;
    int nxt,pre;
};

node a[1000100];
int nxt[1000100],pre[1000100],c[1000100],b[1000100];
int s[1000100],tot;

void del(int x)
{
    a[a[x].pre].nxt=a[x].nxt;
    a[a[x].nxt].pre=a[x].pre;
}
void merge(int x)
{
    a[a[x].pre].nxt=a[x].nxt;
    a[a[x].nxt].pre=a[x].pre;
    a[a[x].pre].cnt+=a[x].cnt;
}
int main()
{
    freopen("wota.in", "r", stdin);
    freopen("wota.out", "w", stdout);

    int n,pos=1,u=0;

    cin>>n; c[0]=-1;
    for(int i=1; i<=n; i++)
    scanf("%d", &c[i]), s[i]=c[i];

    sort(s+1, s+1+n);
    tot=unique(s+1, s+1+n)-s-1;

    for(int i=1; i<=n; i++)
    {
        c[i]=lower_bound(s+1, s+1+tot, c[i])-s;
        nxt[b[c[i]]]=i; pre[i]=b[c[i]]; b[c[i]]=i;
        if(c[i]!=c[i-1])
        {
            a[u].cnt=i-pos;
            a[u].pos=pos;
            a[u].col=c[pos];
            pos=i; ++u;
        }
    }
    a[u].cnt=n+1-pos; a[u].pos=pos; a[u].col=c[pos];

    for(int i=0; i<u; i++) a[i].nxt=i+1;
    for(int i=1; i<=u; i++) a[i].pre=i-1;

    while(a[0].nxt)
    {
        for(int x=a[0].nxt; x; x=a[x].nxt)
        {
            printf("%d ", a[x].pos);
            nxt[pre[a[x].pos]]=nxt[a[x].pos];
            pre[nxt[a[x].pos]]=pre[a[x].pos];
            a[x].pos=nxt[a[x].pos];
            --a[x].cnt;
        }
        
        for(int x=a[0].nxt; x; x=a[x].nxt) if(!a[x].cnt) del(x);
        for(int x=a[0].nxt; x&&a[x].nxt; x=a[x].nxt)
        while(a[x].nxt&&a[x].col==a[a[x].nxt].col)
        merge(a[x].nxt);

        putchar('\n');
    }
    fclose(stdin); fclose(stdout);
    return 0;
}

T4

这边提供一个与出题人不一样的解法

让求最大值，发现是异或操作，二进制下不进位，只需二进制按位从高到低考虑即可

假设我们答案在考虑第 \(i\) 位是否为 \(1\)

显然我们只需让所有的数该二进制位下中存在一个 \(1\) ,其他都为 \(0\) 就好，这样在保证答案的情况下让数尽可能小

让哪一个为 \(1\) 呢

显然让剩余数最大的多这一个 \(1\) 即可

用堆维护这个过程即可

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int T;
int n,x[200100];
priority_queue<int>q;
signed main()
{
    cin>>T;
    while(T--)
    {
        cin>>n;
        while(!q.empty()) q.pop();
        for(int i=1;i<=n;i++) cin>>x[i],q.push(x[i]);
        int ans=0;
        for(int i=32;i>=0;i--)
        {
            if((1ll<<i)<=q.top())
            {
                ans+=(1ll<<i);
                int y=q.top()-(1ll<<i);q.pop();
                q.push(y);
            }
        }
        cout<<ans<<endl;
    }
    return 0;
}

再给一下出题人的题解

全部塞入堆种，每次判断最大的和次大的，如果二进制最高位相同，那么一个就是取最高位 \(1000...\) ，
另一个取 \(01111...\) ，此时最大，直接跳出。否则最大的取最高位，并减掉最高位后放回堆。

重复这个过程，直到跳出或没有两个不为零的元素。

点击查看代码

#include<bits/stdc++.h>
using namespace std;

priority_queue<int> pq;
int ans;

void work()
{
    int n;

    cin>>n; ans=0;
    for(int i=1; i<=n; i++)
    {
        int x;
        scanf("%d", &x);
        pq.push(x);
    }

    while(pq.size()>1)
    {
        int x=pq.top(); pq.pop();
        int y=pq.top(); pq.pop();
        int lx=log2(x)+1,ly=log2(y)+1;
        if(lx==ly)
        {
            ans|=(1<<lx)-1;
            break;
        }
        else
        {
            ans|=x&~((1<<ly)-1);
            x-=x&~((1<<ly)-1);
            if(x) pq.push(x);
            pq.push(y);
        }
    }
    while(pq.size()) { ans|=pq.top(); pq.pop(); }
    cout<<ans<<"\n";
}
int main()
{
    freopen("starryriver.in", "r", stdin);
    freopen("starryriver.out", "w", stdout);
    int t;
    cin>>t;
    while(t-->0) work();
    fclose(stdin); fclose(stdout);
    return 0;
}