一个神奇的题单
watevrCTF2019 Swedish_RSA 30
多项式RSA的模板
在GF(p),先生成两个不可约多项式P,Q,然后N=PQ,在N的商环上,\(c=m^e\)
exp
p=
e=
R.<y>=PolynomialRing(GF(p))
N=
S.<x>=R.quotient(N)
c=
P,Q=N.factor()
print(P)
print(Q)
phi=(pow(p,65)-1)*(pow(p,112)-1) //P不可约,所有deg小于等于P的都没有公根,然后phi是积性函数(能这么理解吗...)
d=inverse_mod(e,phi)
m=c^d
print("".join([chr(c) for c in m.list()]))
De1CTF2020 NLFSR 30
题目描述
点击查看代码
from flag import a, b, c, d, flag
assert flag == "De1CTF{" + ''.join([hex(i)[2:] for i in [a, b, c, d]]) + "}"
assert [len(bin(i)[2:]) for i in [a, b, c, d]] == [19, 19, 13, 6]
ma, mb, mc, md = 0x505a1, 0x40f3f, 0x1f02, 0x31
def lfsr(r, m): return ((r << 1) & 0xffffff) ^ (bin(r & m).count('1') % 2)
def combine():
global a, b, c, d
a = lfsr(a, ma)
b = lfsr(b, mb)
c = lfsr(c, mc)
d = lfsr(d, md)
[ao, bo, co, do] = [i & 1 for i in [a, b, c, d]]
return (ao*bo) ^ (bo*co) ^ (bo*do) ^ co ^ do
def genkey(nb):
s = ''
for i in range(nb*8):
s += str(combine())
open("data", "w+").write(s)
genkey(128*1024)
题目分析
用四个LFSR拼了一个非线性组合生成器,考虑相关系数攻击。若LFSR输出为$ a_1,a_2 \cdots a_n $ ,最终输出为\(b\),则相关系数\(p_i\)为考虑所有情况,\(a_i=b\) 的概率,有一个LFSR的相关系数大于0.53
判定相关系数
点击查看代码
def calc() :
aa,bb,cc,dd=0,0,0,0
for a in range(0,2) :
for b in range(0, 2):
for c in range(0, 2):
for d in range(0, 2):
mk=(a*b) ^ (b*c) ^ (b*d) ^ c ^ d
aa+=(a^mk)^1
bb += (b ^ mk) ^ 1
cc += (c ^ mk) ^ 1
dd += (d ^ mk) ^ 1
print(aa/16,bb/16,cc/16,dd/16)
进行快速相关攻击,这道题初始状态比较小,可以直接暴力枚举a,然后将LFSR生成的结果和combine的结果对比,计算出相关系数最接近的情况作为a。然后确定a的LFSR,继续计算b,c,d的相关系数,以此类推
当初始状态大一些时,paper,算是翻译了一遍。不太能看懂,再看看
在Linux环境下有可以用的脚本
爆破a的exp
点击查看代码
from tqdm import trange
def lfsr(r, m): return ((r << 1) & 0xffffff) ^ (bin(r & m).count('1') % 2)
def guess(beg, end, num, mask):
f = open('', 'r')
data = f.read()[:1600]
f.close()
now = 800
res = 0
for i in trange(beg, end):
r = i
cnt = 0
base = num * 6
for j in range(num * 8):
r = lfsr(r, mask)
lastbit = r & 1
if lastbit == int(data[j], 10):
cnt = cnt + 1
if abs(cnt-base) < now :
now = abs(cnt-base)
res = i
print(res)
guess(pow(2, 18), pow(2, 19), 100, 0x505a1)
SCTF2020 Lattice 30
点击查看代码
from base64 import b16encode
Zx.<x> = ZZ[]
n = 109
q = 2048
p = 3
Df = 9
Dg = 10
Dr = 11
def mul(f,g):
return (f * g) % (x^n-1)
#f对q取模并将系数变小
def bal_mod(f,q):
g = list(((f[i] + q//2) % q) - q//2 for i in range(n))
return Zx(g)
#rand一个deg为d,系数为1或-1的多项式
def random_poly(d):
assert d <= n
result = n*[0]
for j in range(d):
while True:
r = randrange(n)
if not result[r]: break
result[r] = 1-2*randrange(2)
return Zx(result)
#返回modp意义下f的逆
def inv_mod_prime(f,p):
T = Zx.change_ring(Integers(p)).quotient(x^n-1)
return Zx(lift(1 / T(f)))
#返回modq意义下f的逆,q为2的幂
def inv_mod_powerof2(f,q):
assert q.is_power_of(2)
g = inv_mod_prime(f,2)
while True:
r = bal_mod(mul(g,f),q)
if r == 1: return g
g = bal_mod(mul(g,2 - r),q)
def keygen():
f = random_poly(Df)
while True:
try:
fp = inv_mod_prime(f,p)
fq = inv_mod_powerof2(f,q)
break
except:
f = random_poly(Df)
g = random_poly(Dg)
h = bal_mod(p * mul(fq,g),q)
pub_key = h
pri_key = [f,fp]
return pub_key,pri_key
def encrypt(m,h):
r = random_poly(Dr)
e = bal_mod(mul(h,r) + m,q)
return e
if __name__ == '__main__':
pub_key,pri_key = keygen()
flag=b'SCTF{***********}'[5:-1]
m = Zx(list(bin(int(b16encode(flag), 16))[2:]))
print(m)
e = encrypt(m,pub_key)
print('pub_key=')
print(pub_key)
print('e=')
print(e)
#pub_key=
#510*x^108 - 840*x^107 - 926*x^106 - 717*x^105 - 374*x^104 - 986*x^103 + 488*x^102 + 119*x^101 - 247*x^100 + 34*x^99 + 751*x^98 - 44*x^97 - 257*x^96 - 749*x^95 + 648*x^94 - 280*x^93 - 585*x^92 - 347*x^91 + 357*x^90 - 451*x^89 - 15*x^88 + 638*x^87 - 624*x^86 - 458*x^85 + 216*x^84 + 36*x^83 - 199*x^82 - 655*x^81 + 258*x^80 + 845*x^79 + 490*x^78 - 272*x^77 + 279*x^76 + 101*x^75 - 580*x^74 - 461*x^73 - 614*x^72 - 171*x^71 - 1012*x^70 + 71*x^69 - 579*x^68 + 290*x^67 + 597*x^66 + 841*x^65 + 35*x^64 - 545*x^63 + 575*x^62 - 665*x^61 + 304*x^60 - 900*x^59 + 428*x^58 - 992*x^57 - 241*x^56 + 953*x^55 - 784*x^54 - 730*x^53 - 317*x^52 + 108*x^51 + 180*x^50 - 881*x^49 - 943*x^48 + 413*x^47 - 898*x^46 + 453*x^45 - 407*x^44 + 153*x^43 - 932*x^42 + 262*x^41 + 874*x^40 - 7*x^39 - 364*x^38 + 98*x^37 - 130*x^36 + 942*x^35 - 845*x^34 - 890*x^33 + 558*x^32 - 791*x^31 - 654*x^30 - 733*x^29 - 171*x^28 - 182*x^27 + 644*x^26 - 18*x^25 + 776*x^24 + 845*x^23 - 675*x^22 - 741*x^21 - 352*x^20 - 143*x^19 - 351*x^18 - 158*x^17 + 671*x^16 + 609*x^15 - 34*x^14 + 811*x^13 - 674*x^12 + 595*x^11 - 1005*x^10 + 855*x^9 + 831*x^8 + 768*x^7 + 133*x^6 - 436*x^5 + 1016*x^4 + 403*x^3 + 904*x^2 + 874*x + 248
#e=
#-453*x^108 - 304*x^107 - 380*x^106 - 7*x^105 - 657*x^104 - 988*x^103 + 219*x^102 - 167*x^101 - 473*x^100 + 63*x^99 - 60*x^98 + 1014*x^97 - 874*x^96 - 846*x^95 + 604*x^94 - 649*x^93 + 18*x^92 - 458*x^91 + 689*x^90 + 80*x^89 - 439*x^88 + 968*x^87 - 834*x^86 - 967*x^85 - 784*x^84 + 496*x^83 - 883*x^82 + 971*x^81 - 242*x^80 + 956*x^79 - 832*x^78 - 587*x^77 + 525*x^76 + 87*x^75 + 464*x^74 + 661*x^73 - 36*x^72 - 14*x^71 + 940*x^70 - 16*x^69 - 277*x^68 + 899*x^67 - 390*x^66 + 441*x^65 + 246*x^64 + 267*x^63 - 395*x^62 + 185*x^61 + 221*x^60 + 466*x^59 + 249*x^58 + 813*x^57 + 116*x^56 - 100*x^55 + 109*x^54 + 579*x^53 + 151*x^52 + 194*x^51 + 364*x^50 - 413*x^49 + 614*x^48 + 367*x^47 + 758*x^46 + 460*x^45 + 162*x^44 + 837*x^43 + 903*x^42 + 896*x^41 - 747*x^40 + 410*x^39 - 928*x^38 - 230*x^37 + 465*x^36 - 496*x^35 - 568*x^34 + 30*x^33 - 158*x^32 + 687*x^31 - 284*x^30 + 794*x^29 - 606*x^28 + 705*x^27 - 37*x^26 + 926*x^25 - 602*x^24 - 442*x^23 - 523*x^22 - 260*x^21 + 530*x^20 - 796*x^19 + 443*x^18 + 902*x^17 - 210*x^16 + 926*x^15 + 785*x^14 + 440*x^13 - 572*x^12 - 268*x^11 - 217*x^10 + 26*x^9 + 866*x^8 + 19*x^7 + 778*x^6 + 923*x^5 - 197*x^4 - 446*x^3 - 202*x^2 - 353*x - 852
题目分析
lattice攻击NTRU

exp
点击查看代码
p =
q =
n =
Zx.<x> = ZZ[]
e =
h =
def inv_mod_prime(f,p):
T = Zx.change_ring(Integers(p)).quotient(x^n-1)
return Zx(lift(1 / T(f)))
def mul(f,g):
return (f * g) % (x^n-1)
def bal_mod(f,q):
g = list(((f[i] + q//2) % q) - q//2 for i in range(n))
return Zx(g)
def decrypt(e,pri_key):
f,fp = pri_key
a = bal_mod(mul(e,f),q)
d = bal_mod(mul(a,fp),p)
return d
def get_key():
for j in range(2 * n):
try:
f = Zx(list(M[j][:n]))
fp = inv_mod_prime(f,p)
return (f,fp)
except:
pass
return (f,f)
M = matrix(ZZ, 2*n, 2*n)
hh = h.list()
for i in range(n): M[i,i] = 1
for i in range(n,2*n): M[i,i] = q
for i in range(n):
for j in range(n):
M[i,j+n] = hh[(n-i+j) % n]
M = M.LLL()
key = get_key()
l = decrypt(e, key).list()
flag = bytes(l)
print(flag)
NCTF2019 easy_RSA 60
AMM算法模板
点击查看代码
from tqdm import trange
from Crypto.Util.number import *
from gmpy2 import *
import time
import random
c =
p =
q =
e =
def AMM(o, r, q):
start = time.time()
g = GF(q)
o = g(o)
p = g(random.randint(1, q))
while p ^ ((q-1) // r) == 1:
p = g(random.randint(1, q))
print('[+] Find p:{}'.format(p))
t = 0
s = q - 1
while s % r == 0:
t += 1
s = s // r
print('[+] Find s:{}, t:{}'.format(s, t))
k = 1
while (k * s + 1) % r != 0:
k += 1
alp = (k * s + 1) // r
print('[+] Find alp:{}'.format(alp))
a = p ^ (r**(t-1) * s)
b = o ^ (r*alp - 1)
c = p ^ s
h = 1
for i in range(1, t):
d = b ^ (r^(t-1-i))
if d == 1:
j = 0
else:
print('[+] Calculating DLP...')
j = - discrete_log(d, a)
print('[+] Finish DLP...')
b = b * (c^r)^j
h = h * c^j
c = c^r
result = o^alp * h
end = time.time()
print("Finished in {} seconds.".format(end - start))
print('Find one solution: {}'.format(result))
return result
def nanacrt(a,m) :
if(m[0]==0 or m[1]==0) :
return 0
N=m[0]*m[1]
return (a[0]*m[1]%N*invert((N//m[0]),m[0])%N+a[1]*m[0]%N*invert((N//m[1]),m[1])%N)%N
lis1=set()
lis2=set()
lis1.add(rt1)
lis2.add(rt2)
while(len(lis1)<e) :
np=pow(random.randint(0,p-1),(p-1)//e,p)*rt1%p
lis1.add(np)
while(len(lis2)<e) :
np=pow(random.randint(0,q-1),(q-1)//e,q)*rt2%q
lis2.add(np)
print(len(lis1),len(lis2))
for i in lis1 :
for j in lis2 :
mk1=[]
mk1.append(int(i))
mk1.append(int(j))
mk2=[]
mk2.append(int(p))
mk2.append(int(q))
nf=nanacrt(mk1,mk2)
if(long_to_bytes(nf).find(b'NCTF')) :
print(long_to_bytes(nf))
watevrCTF2019 ECC_RSA 50
题目描述
点击查看代码
from fastecdsa.curve import P521 as Curve
from fastecdsa.point import Point
from Crypto.Util.number import bytes_to_long, isPrime
from os import urandom
from random import getrandbits
def gen_rsa_primes(G):
urand = bytes_to_long(urandom(521//8))
while True:
s = getrandbits(521) ^ urand
Q = s*G
if isPrime(Q.x) and isPrime(Q.y):
print("ECC Private key:", hex(s))
print("RSA primes:", hex(Q.x), hex(Q.y))
print("Modulo:", hex(Q.x * Q.y))
return (Q.x, Q.y)
flag = int.from_bytes(input(), byteorder="big")
ecc_p = Curve.p
a = Curve.a
b = Curve.b
Gx = Curve.gx
Gy = Curve.gy
G = Point(Gx, Gy, curve=Curve)
e = 0x10001
p, q = gen_rsa_primes(G)
n = p*q
file_out = open("downloads/ecc-rsa.txt", "w")
file_out.write("ECC Curve Prime: " + hex(ecc_p) + "\n")
file_out.write("Curve a: " + hex(a) + "\n")
file_out.write("Curve b: " + hex(b) + "\n")
file_out.write("Gx: " + hex(Gx) + "\n")
file_out.write("Gy: " + hex(Gy) + "\n")
file_out.write("e: " + hex(e) + "\n")
file_out.write("p * q: " + hex(n) + "\n")
c = pow(flag, e, n)
file_out.write("ciphertext: " + hex(c) + "\n")
'''
ECC Curve Prime: 0x1ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
Curve a: -0x3
Curve b: 0x51953eb9618e1c9a1f929a21a0b68540eea2da725b99b315f3b8b489918ef109e156193951ec7e937b1652c0bd3bb1bf073573df883d2c34f1ef451fd46b503f00
Gx: 0xc6858e06b70404e9cd9e3ecb662395b4429c648139053fb521f828af606b4d3dbaa14b5e77efe75928fe1dc127a2ffa8de3348b3c1856a429bf97e7e31c2e5bd66
Gy: 0x11839296a789a3bc0045c8a5fb42c7d1bd998f54449579b446817afbd17273e662c97ee72995ef42640c550b9013fad0761353c7086a272c24088be94769fd16650
e: 0x10001
p * q: 12916538708895236593179535507652696958130212902754938727546178509610568654166129500188100142747506875538155738050834024841293249875243322231997953335130773335593387031913128963790434108123650368664271877756430432011758177188901760143619102842627935254653509129413728763871069738643074735737955568513819337277682319
ciphertext: 0x3862c872480bdd067c0c68cfee4527a063166620c97cca4c99baff6eb0cf5d42421b8f8d8300df5f8c7663adb5d21b47c8cb4ca5aab892006d7d44a1c5b5f5242d88c6e325064adf9b969c7dfc52a034495fe67b5424e1678ca4332d59225855b7a9cb42db2b1db95a90ab6834395397e305078c5baff78c4b7252d7966365afed9e
'''
题目分析
法一:用椭圆曲线生成了rsa的私钥。然而直接factordb分解n即可得到p,q,令人忍俊不禁
法二:
椭圆曲线上的点满足\(y^2 \equiv x^3+ax+b(mod\;p)\)
p,q在E上,构造方程\(n^2 \equiv (x^3+ax+b)x^2 (mod\;p)\),直接扔到sagemath里解
Other
感觉这pq也没什么特点,yafu试了一下,短时间跑不出来,原来是factordb专门收录了这个题的n导致的
难道这就是yafu里的ecm吗?有时间去研究一下
NPUCTF2020 baby_LCG 55
题目描述
给了一个LCG,有\(x_i=(x_{i-1}*a+b)\; mod \; m\),给出了\(a,b,m\)以及\(x_1\)到\(x_{20}\)的高位,还原\(x_0\)
点击查看代码
from Crypto.Util.number import *
from Crypto.Cipher import AES
from secret import flag
class LCG:
def __init__(self, bit_length):
m = getPrime(bit_length)
a = getRandomRange(2, m)
b = getRandomRange(2, m)
seed = getRandomRange(2, m)
self._key = {'a': a, 'b': b, 'm': m}
self._state = seed
def next(self):
self._state = (self._key['a'] * self._state + self._key['b']) % self._key['m']
return self._state
def export_key(self):
return self._key
def gen_lcg():
rand_iter = LCG(128)
key = rand_iter.export_key()
f = open("key", "w")
f.write(str(key))
return rand_iter
def leak_data(rand_iter):
f = open("old", "w")
for i in range(20):
f.write(str(rand_iter.next() >> 64) + "\n")
return rand_iter
def encrypt(rand_iter):
f = open("ct", "wb")
key = rand_iter.next() >> 64
key = (key << 64) + (rand_iter.next() >> 64)
key = long_to_bytes(key).ljust(16, b'\x00')
iv = long_to_bytes(rand_iter.next()).ljust(16, b'\x00')
cipher = AES.new(key, AES.MODE_CBC, iv)
pt = flag + (16 - len(flag) % 16) * chr(16 - len(flag) % 16)
ct = cipher.encrypt(pt.encode())
f.write(ct)
def main():
rand_iter = gen_lcg()
rand_iter = leak_data(rand_iter)
encrypt(rand_iter)
if __name__ == "__main__":
main()
'''
{'b': 153582801876235638173762045261195852087, 'a': 107763262682494809191803026213015101802, 'm': 226649634126248141841388712969771891297}
7800489346663478448
11267068470666042741
5820429484185778982
6151953690371151688
548598048162918265
1586400863715808041
7464677042285115264
4702115170280353188
5123967912274624410
8517471683845309964
2106353633794059980
11042210261466318284
4280340333946566776
6859855443227901284
3149000387344084971
7055653494757088867
5378774397517873605
8265548624197463024
2898083382910841577
4927088585601943730
'''
题目分析
比较好想到将\(l_i\)作为规约出的向量
Other
NPUCTF2020 Mersenne twister 55
题目描述
点击查看代码
from hashlib import *
from itertools import *
from binascii import hexlify , unhexlify
from flag import flag ,seed
assert len(flag) == 26
assert flag[:7] == 'npuctf{'
assert flag[-1] == '}'
XOR = lambda s1 ,s2 : bytes([x1 ^ x2 for x1 ,x2 in zip(s1 , s2)])
class mt73991:
def __init__(self , seed):
self.state = [seed] + [0] * 232
self.flag = 0
self.srand()
self.generate()
def srand(self):
for i in range(232):
self.state[i+1] = 1812433253 * (self.state[i] ^ (self.state[i] >> 27)) - i
self.state[i+1] &= 0xffffffff
def generate(self):
for i in range(233):
y = (self.state[i] & 0x80000000) | (self.state[(i+1)%233] & 0x7fffffff)
temp = y >> 1
temp ^= self.state[(i + 130) % 233]
if y & 1:
temp ^= 0x9908f23f
self.state[i] = temp
def getramdanbits(self):
if self.flag == 233:
self.generate()
self.flag = 0
bits = self.Next(self.state[self.flag]).to_bytes(4 , 'big')
self.flag += 1
return bits
def Next(self , tmp):
tmp ^= (tmp >> 11)
tmp ^= (tmp << 7) & 0x9ddf4680
tmp ^= (tmp << 15) & 0xefc65400
tmp ^= (tmp >> 18) & 0x34adf670
return tmp
def encrypt(key , plain):
tmp = md5(plain).digest()
return hexlify(XOR(tmp , key))
if __name__ == "__main__":
flag = flag.encode()
random = mt73991(seed)
f = open('./cipher.txt' , 'wb')
for i in flag:
key = b''.join([random.getramdanbits() for _ in range(4)])
cipher = encrypt(key , chr(i).encode())
f.write(cipher)
cef4876036ee8b55aa59bca043725bf350a5e491debdef7ef7d63e9609a288ca1e2c82a7fe566bd8709e73c8d495ea504a486ed11189faf8e6fb35617e47d2d1ad5e4783e96afeaae9f7104ec477fb39fe4ec619bf58289709e15c4449f03fc51cba918cd0ebfdc12376b41e7815406482733b3b200826b6c78d86563edaea94dccf459a4291517a4b8367d7b4a53aeecd7e0accf661bfc726f5ba62e1c0e04100108ad32e7d5711f780185cba5cf31d328bee84066be4ab9582cf9d4bfe3c6f96a7732e1c37d800c90fd46277147f0a26c149dcd5eeb0f2df0c075627bc220be5eefdd67186056ac28c21e155a7f247664aaecdb498134de274df10114d1f06f84dd21820f150d69c9439d909dec0f5ccfeab61b62db2ea91d31bc8163ff16c7f458006bd5ac4a5f5bfae2770b23ccfb7195b76aa0a9aa146831667a7b9fe08c19e691afadccb3ca5169ef3fabaa3dad47d536e89ed4cee6f788bc969c3ad3137850ebfc46a73af2b0c036c3da4b4a16506f499445c604dd73eeb846a52f881515a3ad0ab448b4f9ed3e0ab1fffac60b223dde6450ba6198e90e14de107aaf2
题目分析
诈骗题,前7*16位的state可以恢复,然后就没有想法了,结果wp是爆破seed,然后用state验证对不对...有精神的!
Other
有更好的做法
“2020.4.22:赛后出题人 shallow 师傅告诉我这题 seed 不用爆破可以推出来…已知明文的 “}” 刚好用到了第 103 个随机数。tql,我根本没想到能凑这么巧,我好菜啊… orz”
确实没想到,逆向twist基本直接copy脚本,仔细观察一下twist
mk=0x9908f23f
y = (self.state[i] & 0x80000000) | (self.state[(i+1)%233] & 0x7fffffff)
temp = y >> 1
temp ^= self.state[(i + 130) % 233]
if y & 1: temp ^= mask
self.state[i] = temp
\(现在已知twist后的state1[0]和state1[103]\),\(观察可知state1[103]由state0[103]的最高位和state0[104]的后面组成\),\(然后异或了state1[0]\),\(然后根据最低位决定要不要异或mask\),\(枚举state0[103]的最高位和是否异或mask\),\(计算出可能的4个state0[104]\)
点击查看代码
def guess() :
mk=s103
mask=0x9908f23f
mk=mk^mask^s0
mk=mk<<1|1
rec_104(mk&0x7fffffff)
rec_104((mk&0x7fffffff)|0x80000000)
mk=s103
mk=mk^s0
mk=mk<<1
rec_104((mk&0x7fffffff))
rec_104((mk&0x7fffffff) | 0x80000000)
\(然后根据state0[104]恢复seed\)
点击查看代码
def rec_104(x) :
mod=0xffffffff+1
state=[0]*145
state[104]=x
for j in range(0,104) :
i=104-j-1
state[i]=(state[i+1]+i)%mod*invert(1812433253,mod)%mod
state[i]=state[i]^(state[i]>>27)
print("seed:",state[0])
return state[0]
seed: 4177179095
seed: 1801895341
seed: 1668245885 11111
seed: 2899787883
其中有一步是逆向$y=x\oplus (x>>i) $,有 \(y \oplus (y>>i)=x\oplus (x>>i) \oplus (x>>i) \oplus (x>>2i)\),所以\(x=\sum_{j=0} \oplus (y>>i*j)\)
WMCTF2020 piece_of_a_cake 65
题目描述
点击查看代码
from Crypto.Util.number import *
from gmpy2 import invert
from hashlib import sha256
import string
import os
import random
from secret import flag, e
assert e.bit_length() == 477
BITS = 512
def eat_cake():
p, q = getPrime(BITS), getPrime(BITS)
ph = (p - 1) * (q + 1)
N = p * q
d = invert(e, ph)
print(d)
# 768 bits
cake = getPrime(BITS >> 1 | BITS)
# 1536 bits
q = getPrime(BITS << 1 | BITS)
f = d
g = getPrime(q.bit_length() - f.bit_length() - 1)
f_inv_q = invert(f, q)
h = f_inv_q * g % q
r = getPrime(BITS)
c = (r * h + cake) % q
print(q, h, c)
print(N)
print(pow(cake, 0x10001, N))
answer = int(input("Give me your cake:"))
print("This cake looks delicious!" if cake != answer else flag)
return
def make_cake():
p, q = getPrime(BITS), getPrime(BITS)
N = p * q
ph = (p - 1) * (q + 1)
d = invert(e, ph)
# 256 bits
cake = getPrime(BITS >> 1)
# 1536 bits
q = getPrime(BITS << 1 | BITS)
f = d
g = getPrime(q.bit_length() - f.bit_length() - 1)
f_inv_q = invert(f, q)
h = f_inv_q * g % q
r = getPrime(BITS)
c = (r * h + cake) % q
print(q, h, c)
print(N)
print(pow(cake, d, N))
return
if __name__ == '__main__':
if (proof_of_work()):
print("WELCOME TO MY CAKE GAME!")
print("1.EAT MY CAKE\n2.MAKE A CAKE\n3.EXIT")
op = int(input("What's your choice?\n"))
if op == 1:
print("Here is my cake:")
eat_cake()
elif op == 2:
print("Let's make a big cake!")
make_cake()
elif op == 3:
print("Bye~")
exit()
else:
print("Your choice is so strange!")
exit()
题目分析
感觉是三合一
Step1 Lattice解d
非常经典的问题
\(fh \equiv g(mod \; q)\)
\(fh \equiv g(mod \; q)\)
\(fh+kq=g\)
Step2 lattice based attack on common private
通过Step1解出了d,e相同且很大,可以用论文中的算法
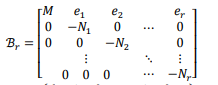
Step3 数论
通过Step2解出了e,现在的问题是
已知\(e,d,n\),有\(ed\equiv 1(mod \;(p-1)(q+1))\),分解\(n\)
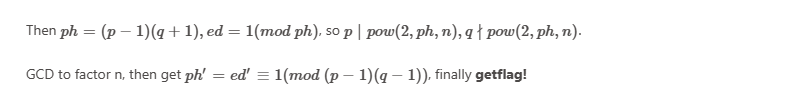
wp给的exp
点击查看代码
def factor_n(e):
q, h, c1, N, c2 = eat_cake()
quotients = rational_to_quotients(h, q)
convergents = convergents_from_quotients(quotients)
for (k, f) in convergents:
p = GCD(int(pow(2, f * e - 1, N) - 1), N)
if p > 1 and p < N:
q = N // p
d = inverse(0x10001, (p - 1) * (q - 1))
cake = pow(c2, d, N)
print(cake)
break
Other
WP在处理Step1的时候用了连分数
\(\frac{h}{q}-\frac{k}{f}=\frac{g}{fq}\)
天翼杯2020 hard_RSA 40
题目描述
点击查看代码
p = getPrime(510)
q = getPrime(510)
r = getPrime(510)
e = 7
m = bytes_to_long(os.urandom(30) + flag)
n = p * q * r
d = invert(e, (p - 1) * (q - 1) * (r - 1))
c = pow(m, e, n)
print(n // p)
print(p)
print(c)
print(hex(d % (1 << 540)))
题目分析
先推柿子
\(ed=1+k(p-1)(q-1)(r-1)\)
\(n=rq,K=k(p-1)\)
\(ed_l\equiv 1+K(n-r-q+1)(mod \; 2^{540})\)
\(ed_lq\equiv -Kq^2+(nK+K+1)q-nK(mod \; 2^{540})\)
\(Kq^2-(nK+K-ed_l+1)q+nK\equiv 0(mod \; 2^{540})\)
e小,枚举k,用solve_mod算出q的低位,再coppersmith一下(不过这道题直接出了)
Other
感觉同时乘p把q变成n是常见操作
De1CTF2020 ECDH 60
题目描述
点击查看代码
import os, random, sys, string
from hashlib import sha256
import SocketServer
import signal
from FLAG import flag
from gmpy2 import invert
from Crypto.Util.number import bytes_to_long, long_to_bytes
q = 0xdd7860f2c4afe6d96059766ddd2b52f7bb1ab0fce779a36f723d50339ab25bbd
a = 0x4cee8d95bb3f64db7d53b078ba3a904557425e2a6d91c5dfbf4c564a3f3619fa
b = 0x56cbc73d8d2ad00e22f12b930d1d685136357d692fa705dae25c66bee23157b8
zero = (0, 0)
def add(p1, p2):
if p1 == zero:
return p2
if p2 == zero:
return p1
(p1x, p1y), (p2x, p2y) = p1, p2
if p1x == p2x and (p1y != p2y or p1y == 0):
return zero
if p1x == p2x:
tmp = (3 * p1x * p1x + a) * invert(2 * p1y, q) % q
else:
tmp = (p2y - p1y) * invert(p2x - p1x, q) % q
x = (tmp * tmp - p1x - p2x) % q
y = (tmp * (p1x - x) - p1y) % q
return (int(x), int(y))
def mul(n, p):
r = zero
tmp = p
while 0 < n:
if n & 1 == 1:
r = add(r, tmp)
n, tmp = n >> 1, add(tmp, tmp)
return r
def pointToString(p):
return "(" + str(p[0]) + "," + str(p[1]) + ")"
Px = 0xb55c08d92cd878a3ad444a3627a52764f5a402f4a86ef700271cb17edfa739ca
Py = 0x49ee01169c130f25853b66b1b97437fb28cfc8ba38b9f497c78f4a09c17a7ab2
P = (Px, Py)
class Task(SocketServer.BaseRequestHandler):
def recvall(self, sz):
try:
r = sz
res = ""
while r > 0:
res += self.request.recv(r)
if res.endswith("\n"):
r = 0
else:
r = sz - len(res)
res = res.strip()
except:
res = ""
return res.strip("\n")
def dosend(self, msg):
try:
self.request.sendall(msg)
except:
pass
def handle(self):
try:
if not self.proof_of_work():
return
signal.alarm(300)
self.secret = random.randint(0, q)
Q = mul(self.secret, P)
self.dosend("Welcome to the ECDH System.\n")
self.dosend("The params are: \n")
self.dosend("q: " + str(q) + "\n")
self.dosend("a: " + str(a) + "\n")
self.dosend("b: " + str(b) + "\n")
self.dosend("P: " + pointToString(P) + "\n")
self.dosend("Q: " + pointToString(Q) + "\n")
self.exchange()
for _ in range(90):
self.dosend("Tell me your choice:\n")
choice = self.recvall(9)
if choice == "Exchange":
self.exchange()
elif choice == "Encrypt":
self.encrypt()
elif choice == "Backdoor":
self.backdoor()
else:
self.dosend("No such choice!\n")
self.dosend("Bye bye~\n")
self.request.close()
except:
self.dosend("Something error!\n")
self.request.close()
def pad(self, m):
pad_length = q.bit_length() * 2 - len(m)
for _ in range(pad_length):
m.insert(0, 0)
return m
def encrypt(self):
self.dosend("Give me your message(hex):\n")
msg = self.recvall(150)
data = [int(i) for i in list('{0:0b}'.format(bytes_to_long(msg.decode("hex"))))]
enc = [data[i] ^ self.key[i % len(self.key)] for i in range(len(data))]
result = 0
for bit in enc:
result = (result << 1) | bit
result = long_to_bytes(result).encode("hex")
self.dosend("The result is:\n")
self.dosend(result + "\n")
def pointToKeys(self, p):
x = p[0]
y = p[1]
tmp = x << q.bit_length() | y
res = self.pad([int(i) for i in list('{0:0b}'.format(tmp))])
return res
def exchange(self):
self.dosend("Give me your key:\n")
self.dosend("X:\n")
x = int(self.recvall(80))
self.dosend("Y:\n")
y = int(self.recvall(80))
key = (x, y)
result = mul(self.secret, key)
self.key = self.pointToKeys(result)
self.dosend("Exchange success\n")
def backdoor(self):
self.dosend("Give me the secret:\n")
s = self.recvall(80)
if int(s) == self.secret:
self.dosend('Wow! How smart you are! Here is your flag:\n')
self.dosend(flag)
else:
self.dosend('Sorry you are wrong!\n')
exit(0)
class ForkedServer(SocketServer.ForkingTCPServer, SocketServer.TCPServer):
pass
if __name__ == "__main__":
HOST, PORT = "0.0.0.0", 8848
server = ForkedServer((HOST, PORT), Task)
server.allow_reuse_address = True
server.serve_forever()
题目分析
当ECDH没有验证公钥是否在椭圆曲线上时,可通过构造低阶曲线上的点进行攻击


 浙公网安备 33010602011771号
浙公网安备 33010602011771号