分治算法乱讲

何为分治

分治（Divide and Conquer），就是把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。——摘自 OI wiki

很眼熟？线段树和分块都有这个思想！

如果你没学过线段树和分块当我没说。

分治实现

根据它的定义，我们很容易就想到递归求解。

void dfs(int l, int r){
    if(可以直接求解){
        ...;
        return;
    }
    int d = (l + r) / 2;// 分成两个子问题
    dfs(l, d);
    dfs(d + 1, r);
}

时间复杂度 \(O(n \times 直接求解的复杂度)\)

根据题目所求的不同而变。

应用 & 例题

分治主要用于静态区间求解一些奇怪的东西。

分治的理解还是得要例题的。这样就可以水字数啦111

题意：

给一个数组 \(𝑎_1,𝑎_2,…,𝑎_𝑛\)，你希望固定尽量少的元素，满足：

  1. 对于剩下未固定的元素 \(𝑎_𝑥\)，它左右都有固定的元素。

  2. 设 \(𝑎_𝑙,𝑎_𝑟\) 是左右两边最靠近它的固定的元素，\(𝑎_𝑙<𝑎_𝑥<𝑎_𝑟\) 或 \(𝑎_𝑙>𝑎_𝑥>𝑎_𝑟\)。

求最少需要固定多少个元素。

保证 \(a_i\) 两两不同。\(1 \le n\le 10^5\)，\(1\le a_i ≤ 10^9\)。

思路：

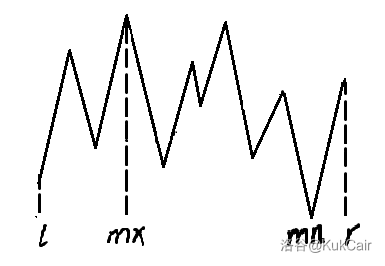
对于一个区间 \([l,r]\)，我们设区间最大值为 \(a_{mx}\)，最小值为 \(a_{mn}\)。

那我们分成三段考虑：\(a_{mn} \sim a_l\)，\(a_l \sim a_r\) 和 \(a_r \sim a_{mx}\)（纵向）。

  • 如果说 \(a_l,a_r\) 刚好就是区间最大、最小值，那么这个区间只需要 \((l,r)\) 这一对固定就行了。

  • 如果说 \(a_l,a_r\) 不包含区间最小值，那么分成 \([l,mn]\) 和 \([mn+1,r]\)。

  • 如果说 \(a_l,a_r\) 不包含区间最大值，那么分成 \([l,mx]\) 和 \([mx+1,r]\)。

题意：

给定一个长度为 \(N\) 的正整数序列 \(A_i\) 。

对于其任意一个连续的子序列 \(A_l,A_{l+1},...,A_r\) ，我们定义其权值 \(W(L,R) = (R-L+1) × \gcd (A_l,...,A_r)\)。

求最大的 \(W(L,R)\)。

\(1 \le A_i \le 10^{12}, 1 \le N \le 100000\)

思路：

我们看到这题，\(n\le 10^5\)。DP 不行；贪心不行；那么大概率就是分治了。

对于一个区间 \([l,r]\)，我们设 \(mid=\dfrac{l+r}{2}\)。

那么如果最大的子序列就在 \([l,mid]\) 或 \([mid+1,r]\) 里，我们就直接递归到 \([l,mid]\) 或 \([mid+1,r]\) 里去。

再考虑横跨 \(mid\) 的情况。

我们在 \([l,mid]\) 这个区间里考虑 \(l_1\)。

  • 如果 \([l_1,mid]\) 的权值等于 \([l_1+1,mid]\) 的权值，肯定会选 \([l_1,mid]\)（长度更长）。

  • 如果 \([l_1,mid]\) 的权值 \(>[l_1+1,mid]\) 的权值，我们将 \(l_1+1\) 放入一个队列，表示 \([l_1+1,mid]\) 的权值最多取到 \(l_1+1\) 这里。

\([mid+1,r]\) 同理。然后枚举队列里的左右端点加贡献即可。

Q：你的权值个数不会很多吗？这样的话“枚举队列里的左右端点加贡献”会超时吧？

A：实际上，权值个数即 \(gcd\) 个数不会超过 \(\log n\) 个，原因：小于 \(n\) 且能被 \(n\) 整除的最大的数字一定小于等于 \(\dfrac{n}2\)，也就说小于 \(n\) 的最大的 \(gcd\) 不超过 \(\dfrac{n}2\)。每次往左边扩大区间范围后的 \(gcd\) 要么等于原来的gcd，要么小于等于原来的 \(\dfrac{gcd}2\)。最多产生 \(\log\) 个新的 \(gcd\)。

拓：决策单调性优化 DP 与分治

如果有四个点 \(a<b<c<d\) 且 \(f(a,d)+f(b,c)\ge f(a,c)+f(b,d)\)，那么函数 \(f\) 满足四边形不等式。

如果一个形如 \(dp_i=min(dp_j+f(j,i))\) 的转移方程满足四边形不等式，那么这个转移方程具有决策单调性。

考虑更好地转移，对于区间 \([l,r]\)，设 \(mid=\dfrac{l+r}2\)，并暴力计算出 \(mid\) 的转移点 \(d_{mid}\)。如果原区间转移范围为 \([L,R]\)，那么可以把它分成两半：

\([l,mid]\) 转移范围在 \([L,d_{mid}]\)，\([mid+1,r]\) 转移范围在 \([d_{mid},R]\)。

分治树只有 \(\log n\) 层，每层的复杂度为 \(O(n)\)，所以时间复杂度 \(O(n \log n)\)。

posted @ 2025-10-24 19:45  KukCair  阅读(9)  评论(0)    收藏  举报