字典树 Trie 乱讲

Trie 是什么

实际上它就是一颗像字典的树，支持插入单词和查询单词个数等操作。

它的边权是某个字符。

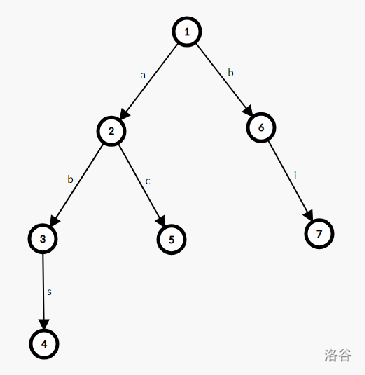
比如上图，插入单词 aca 时，我们就可以在 \(5\) 号节点下新建一个节点，边权为 a。而查询是否单词 abs 时，答案为是，因为存在路径 \(1 \to 2 \to 3 \to 4\) 的边权为 abs。

Trie 的实现

插入 & 删除

插入：对于已有的位置，我们直接就可以在原有基础上加；否则就新建一个节点。

删除同理。

// cnt[u]：1 -> u 这条路径以前有几次走过（记录路径对应单词个数）
// trie[u][x]：节点 u 的孩子中，对应边权为 x 的节点编号
void insert(string s){
	int u = 0;
	for(int i = 0; i < s.size(); i++){
		if(!trie[u][s[i] - 'a' + 1]){ // 没有下一个对应节点，新建一个
			c++;
			trie[u][s[i] - 'a' + 1] = c;
		}
		u = trie[u][s[i] - 'a' + 1]; // 到下一个对应节点
		cnt[u]++; // 将当前节点的权值 + 1
	}
}
void del(string s){
	int u = 0;
	for(int i = 0; i < s.size(); i++){
		u = trie[u][s[i] - 'a' + 1]; // 到下一个对应节点
		cnt[u]--; // 将当前节点的权值 - 1
	}
}

查询个数

这个过程很像插入，但是如果没有下一个对应节点就说明这个单词不存在，直接返回 \(0\)；否则答案为最后一个节点的权值。

void insert(string s){
	int u = 0;
	for(int i = 0; i < s.size(); i++){
		if(!trie[u][s[i] - 'a' + 1]) return 0; // 没有下一个对应节点，也就没有对应单词
		u = trie[u][s[i] - 'a' + 1]; // 到下一个对应节点
	}
	return cnt[u];
}

Trie 的应用

在一些需要求解相同前 / 后缀个数、查找一个字符串是否出现过 / 出现次数时可以用到，但是很少会单独用它。

AC 自动机要用，但我不会。

变式：01 Trie

顾名思义，01Trie 就是只维护 \(0\) 和 \(1\) 的 Trie。

看到 \(0\) 和 \(1\)，很自然地会想到二进制。我们可以以 01Trie 维护最小 / 大异或值一类问题。

实现大体是一样的，直接贴代码吧。

void insert(ll s){
	ll u = 0;
	for(int i = 29; i >= 0; i--){
		bool x = (s >> i) & 1;
		if(!zotrie[u][x]){
			c++;
			zotrie[u][x] = c;
		}
		u = zotrie[u][x];
		cnt[u]++;
	}
}
void del(ll s){
	ll u = 0;
	for(int i = 29; i >= 0; i--){
		bool x = (s >> i) & 1;
		u = zotrie[u][x];
		cnt[u]--;
	}
}
ll querymax(ll s){
	ll ans = 0, u = 0;
	for(int i = 29; i >= 0; i--){
		bool x = (s >> i) & 1;
		ans <<= 1;
		if(cnt[zotrie[u][!x]]){ // 取反是因为异或最大当然要优先不同位位数最高
			ans++;
			u = zotrie[u][!x];
		}
		else u = zotrie[u][x];
	}
	return ans;
}
ll querymin(ll s){
	ll ans = 0, u = 0;
	for(int i = 29; i >= 0; i--){
		bool x = (s >> i) & 1;
		ans <<= 1;
		if(cnt[zotrie[u][x]]){ // 不取反同理
			u = zotrie[u][x];
		}
		else{
			ans++;
			u = zotrie[u][!x];
		}
	}
	return ans;
}

例题

Trie

• Luogu P5629 【AFOI-19】区间与除法

思路：将一个数除以 \(d\) 并向下取整等价于去掉这个数在 \(d\) 进制下的最后一位。

考虑这个匹配的过程，就是将两个数 \(d\) 进制下的最高位对齐，看原数是否是这个数的前缀，很容易想到用 Trie 维护。

可以将消灭一个区间内所有数的最小原数的集合用状压表示，并用 ST 表维护，用按位或合并。

01 Trie

• Luogu P4551 最长异或路径

思路：我们对于每一个数到根节点的异或和进行建 01 Trie。一个数两次异或同一个数不变。

\(u \to v\) 路径上的异或和，可以表示成根到 \(u\) 的异或和异或上根到 \(v\) 的异或和。

答案即为 \(\max{query(xor_i)}\)（\(xor_i\) 表示根节点到节点 \(i\) 的异或和）。