后缀数组
后缀数组
一些定义
子串
字符串 \(s\) 中,截取任意 \(i\le j\) 的一段就是 \(s\) 的子串
后缀
后缀 \(i\) 即 \(\text{suffix}(i)\) 表示从 \(i\) 开始到结尾的子串
后缀数组 sa
\(sa_i\) 表示排名为 \(i\) 的后缀起始位置
排名数组 rk
\(rk_i\) 表示后缀 \(i\) 的排名
求后缀数组
直接快排为 \(O(n^2\log n)\) ,不再赘述。
这里记录复杂度为 \(O(n\log^2 n)\) 或 \(O(n\log n)\) 的倍增算法
主要思路:
每次对长度为 \(2^k\) 的子串进行排序,每一次排序都利用上一次长度为 \(2^{k-1}\) 的子串排名
长度为 \(2^k\) 的子串可以用两个长度为 \(2^{k-1}\) 子串排名作为关键字表示
没有第二关键字直接补 0,当排序后所有排名不同时可以提前结束。
即通过倍增,用子串组合出后缀,双关键字排序优于字符串排序,提高效率

基数排序
在 \(O(n)\) 的时间完成双关键字排序。实际上是两次计数排序
回忆一下计数排序:
- 桶记录次数
- 求前缀和
- 从后往前计算排名
运用到这里来:
\(m\) 表示字符集大小
\(id_i\) 表示第二关键字排名为 \(i\) 的子串位置
\(rk_i\) 表示以 \(i\) 开始的子串排名即第一关键字
按照第二关键字的顺序标号
const int N = 1e5 + 5;
int n, m, t[N], rk[N], sa[N], id[N];
inline void rs() {
for (int i = 1; i <= m; i++) t[i] = 0;
for (int i = 1; i <= n; i++) ++t[rk[i]];
for (int i = 1; i <= m; i++) t[i] += t[i - 1];
for (int i = n; i >= 1; i--) sa[t[rk[id[i]]]--] = id[i], id[i] = 0;
}
倍增
\(old_i\) 表示上一次 \(i\) 的排名
int old[N];
inline int EQ(int x, int y, int k)
{ return old[x] == old[y] && old[x + k] == old[y + k]; }
inline void SA() {
m = 130;
for (int i = 1; i <= n; i++) rk[i] = a[i], id[i] = i;
rs();
for (int k = 1, p; k <= n; k <<= 1) {
p = 0;
for (int i = n - k + 1; i <= n; i++) id[++p] = i;
for (int i = 1; i <= n; i++) if (sa[i] > k) id[++p] = sa[i] - k;
rs(), memcpy(old, rk, sizeof(rk)), p = 0;
for (int i = 1; i <= n; i++) rk[sa[i]] = EQ(sa[i], sa[i - 1], k) ? p : ++p;
if (p == n) break;
m = p;
}
}
分段来看:
m = 130;
for (int i = 1; i <= n; i++) rk[i] = a[i], id[i] = i;
rs();
第一次排序。得到初始排名
p = 0;
for (int i = n - k + 1; i <= n; i++) id[++p] = i;
for (int i = 1; i <= n; i++) if (sa[i] > k) id[++p] = sa[i] - k;
按照第二关键字排序。
- 由于 \([n-k+1,n]\) 没有第二关键字,直接按照顺序加入
- 枚举排名,若 \(sa_i>k\) 说明可以作为别人的第二关键字,加入其对应第一关键字。
按照排名加入,其实已经按照第二关键字排了序
rs(), memcpy(old, rk, sizeof(rk)), p = 0;
for (int i = 1; i <= n; i++) rk[sa[i]] = EQ(sa[i], sa[i - 1], k) ? p : ++p;
排序、计算排名。如果两个关键字旧排名都相同,则新排名也相同。
if (p == n) break;
m = p;
如果排名互不相同,可提前推出。更改值域范围
code
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 1e6 + 5;
int n, m, sa[N], rk[N], id[N], t[N], old[N];
char a[N];
inline void rs() {
for (int i = 1; i <= m; i++) t[i] = 0;
for (int i = 1; i <= n; i++) ++t[rk[i]];
for (int i = 1; i <= m; i++) t[i] += t[i - 1];
for (int i = n; i >= 1; i--) sa[t[rk[id[i]]]--] = id[i], id[i] = 0;
}
inline int EQ(int x, int y, int k)
{ return old[x] == old[y] && old[x + k] == old[y + k]; }
inline void SA() {
m = 130;
for (int i = 1; i <= n; i++) rk[i] = a[i], id[i] = i;
rs();
for (int k = 1, p; k <= n; k <<= 1) {
p = 0;
for (int i = n - k + 1; i <= n; i++) id[++p] = i;
for (int i = 1; i <= n; i++) if (sa[i] > k) id[++p] = sa[i] - k;
rs(), memcpy(old, rk, sizeof(rk)), p = 0;
for (int i = 1; i <= n; i++) rk[sa[i]] = EQ(sa[i], sa[i - 1], k) ? p : ++p;
if (p == n) break;
m = p;
}
}
void put(int x) { if (x > 9) put(x / 10); putchar(x % 10 | 48); }
int main() {
scanf("%s", a + 1);
n = strlen(a + 1);
SA();
for (int i = 1; i <= n; i++) put(sa[i]), putchar(32);
}
最长公共前缀
即 \(\text{LCP}\) ,此处令 \(\text{LCP}(i,j)\) 为 \(\text{suffix}(sa_i)\) 和 \(\text{suffix}(sa_j)\) 的最长公共前缀
有如下几个定义
-
\(height_i=\text{LCP}(i,i-1)\) ,特别地,\(height_1=0\)
即排名相邻的后缀的 \(\text{LCP}\)
-
\(h_i=height_{rk_i}\) ,即 \(i\) 和它前一名的 \(\text{LCP}\)
性质
-
\(\text{LCP}(i,j)=\text{LCP}(j,i)\) , \(\text{LCP}(i,i)=n-sa_i+1\)
-
\(\forall k\in[i,j],\text{LCP}(i,j)=\min(\text{LCP}(i,k),\text{LCP}(k,j))\)
设 \(p=\min(\text{LCP}(i,k),\text{LCP}(k,j))\)
则 \(\text{LCP}(i,k)\ge p,\text{LCP}(k,j)\ge p\)
令 \(\text{suffix}(sa_i)=u,\text{suffix}(sa_j)=v,\text{suffix}(sa_k)=w\)
则 \(u,w\) 前 \(p\) 个字母相同, \(v,w\) 前 \(p\) 个字母相同
因为 \(p=\min(\text{LCP}(i,k),\text{LCP}(k,j))\) ,所以 \(u_{p+1}< w_{p+1}\) 或 \(w_{p+1}<v_{p+1}\) (排名)
所以 \(u_{p+1}\ne v_{p+1}\) ,\(\text{LCP}(i,j)=p\)
-
\(\text{LCP}(i,j)=\min_{k=i+1}^j height_k\)
证明:用上一个性质
\[\begin{aligned} \text{LCP}(i,j)&=\min(\text{LCP}(i,i+1),\text{LCP}(i+1,j))\\ &=\min(\text{LCP}(i,i+1),\min(\text{LCP}(i+1,i+2),\text{LCP}(i+2,j))\\ &\cdots\\ &=\min_{k=i+1}^j\text{LCP}(k,k-1)=\min_{k=i+1}^j height_k \end{aligned} \]

求法
还记得 \(h_i=height_{rk_i}\) 吗,它有关键性质:
假设后缀 \(i-1\) 前一名为后缀 \(j\) ,分别删去首字母后得到后缀 \(j+1\) 和后缀 \(i\)
此时后缀 \(j+1\) 一定在后缀 \(i\) 前面,且二者最长公共前缀为 \(h_{i-1}-1\)
由先前的性质 ,可得 \(h_{i-1}-1\) 是一些连续 \(h\) 的 \(\min\) 值,包括了 \(h_i\)
所以 \(h_i\ge h_{i-1}-1\)
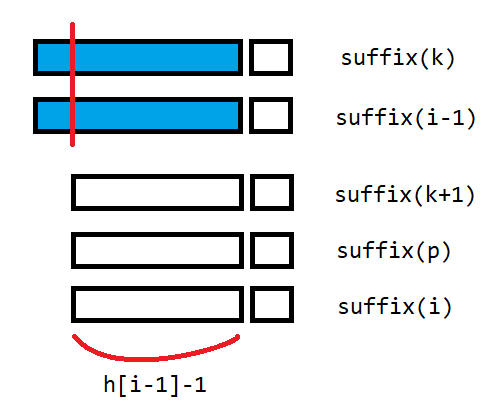
按照从小到大的顺序计算 \(h_i\) ,暴力后移那么复杂度是 \(O(n)\) 的
实现时:没有必要开出 \(h\) 数组,用变量记录,然后赋值 \(height_{rk_i}\) 即可
int h[N];
// h is height
void get() {
for (int i = 1, j, k = 0; i <= n; h[rk[i++]] = k)
for (k ? --k : 0, j = sa[rk[i] - 1]; a[i + k] == a[j + k]; k++);
}
应用
最长公共前缀
询问任意两个后缀的最长公共前缀。
求出 \(height\) ,用 RMQ 解决,\(O(n\log n)\)
单个字符串
不可重叠最长重复子串
二分答案,答案变成判定性问题。
将 \(height\) 分为连续的组,如果有连续的一段 \(height\ge mid\) ,且 \(\max(sa_i)-\min(sa_i)>mid\)
说明存在长度为 \(mid\) 且不重叠的重复子串。
对 \(height\) 分组的方法很重要。
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 50005;
int n, m = 200, a[N], rk[N], id[N], old[N], sa[N], t[N], h[N];
inline bool EQ(int x, int y, int k) { return old[x] == old[y] && old[x + k] == old[y + k]; }
inline void bui() {
for (int i = 1; i <= n; i++) ++t[rk[i] = a[i]];
for (int i = 1; i <= m; i++) t[i] += t[i - 1];
for (int i = n; i >= 1; i--) sa[t[rk[i]]--] = i;
for (int k = 1, p; k <= n; m = p, k <<= 1) {
p = 0;
for (int i = n - k + 1; i <= n; i++) id[++p] = i;
for (int i = 1; i <= n; i++) if (sa[i] > k) id[++p] = sa[i] - k;
for (int i = 1; i <= m; i++) t[i] = 0;
for (int i = 1; i <= n; i++) ++t[rk[i]];
for (int i = 1; i <= m; i++) t[i] += t[i - 1];
for (int i = n; i >= 1; i--) sa[t[rk[id[i]]]--] = id[i], id[i] = 0;
memcpy(old, rk, sizeof(rk)), p = 0;
for (int i = 1; i <= n; i++) rk[sa[i]] = EQ(sa[i], sa[i - 1], k) ? p : ++p;
if (p == n) break;
}
for (int i = 1, j, k = 0; i <= n; h[rk[i++]] = k)
for (k ? --k : 0, j = sa[rk[i] - 1]; a[i + k] == a[j + k]; k++);
}
int chk(int x) {
int mx = sa[1], mn = sa[1];
for (int i = 2; i <= n; i++) {
if (h[i] < x) mx = mn = sa[i];
else {
mx = max(mx, sa[i]);
mn = min(mn, sa[i]);
if (mx - mn > x) return 1;
}
}
return 0;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i < n; i++) a[i] = 90 + a[i + 1] - a[i];
a[n--] = 0;
bui();
int L = 0, R = n, mid, ans = 0;
while (L <= R) {
mid = L + R >> 1;
if (chk(mid)) ans = mid, L = mid + 1;
else R = mid - 1;
}
printf("%d", ans > 3 ? ans + 1 : 0);
}
子串个数
求不相同的子串的个数
每一个后缀的贡献是 \(n-sa_i+1-height_i\)
回文子串
字符串反转接在原字符串后面,用 # 分隔。
枚举回文串中心,分长度为奇数、偶数计算,\(O(n\log n)\)
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 20005;
int n, mid, m = 200, rk[N], sa[N], id[N], old[N], h[N], t[N], f[N][20], lg[N], ans, St;
char a[N];
inline void rs() {
for (int i = 1; i <= m; i++) t[i] = 0;
for (int i = 1; i <= n; i++) ++t[rk[i]];
for (int i = 1; i <= m; i++) t[i] += t[i - 1];
for (int i = n; i >= 1; i--) sa[t[rk[id[i]]]--] = id[i], id[i] = 0;
}
inline int EQ(int x, int y, int k)
{ return old[x] == old[y] && old[x + k] == old[y + k]; }
inline void bui() {
m = 200;
for (int i = 1; i <= n; i++) rk[i] = a[i], id[i] = i;
rs();
for (int k = 1, p; k <= n; m = p, k <<= 1) {
p = 0;
for (int i = n - k + 1; i <= n; i++) id[++p] = i;
for (int i = 1; i <= n; i++) if (sa[i] > k) id[++p] = sa[i] - k;
rs(), memcpy(old, rk, sizeof(rk)), p = 0;
for (int i = 1; i <= n; i++) rk[sa[i]] = EQ(sa[i], sa[i - 1], k) ? p : ++p;
if (p == n) break;
}
for (int i = 1, j, k = 0; i <= n; h[rk[i++]] = k)
for (k ? k-- : 0, j = sa[rk[i] - 1]; a[i + k] == a[j + k]; k++);
}
inline int rmq(int l, int r) {
if (r == l) return h[l];
register int k = lg[r - l + 1];
return min(f[l][k], f[r - (1 << k) + 1][k]);
}
inline int lcp(int i, int j) {
if (rk[i] > rk[j]) i ^= j ^= i ^= j;
return rmq(rk[i] + 1, rk[j]);
}
int main() {
scanf("%s", a + 1);
n = strlen(a + 1);
a[mid = n + 1] = '#';
for (int i = 1; i <= n; i++) a[mid + i] = a[n - i + 1];
n = n * 2 + 1, bui();
for (int i = 1; i <= n; i++) f[i][0] = h[i];
for (int i = 2; i <= n; i++) lg[i] = lg[i >> 1] + 1;
for (int j = 1; j <= 15; j++)
for (int i = 1; i + (1 << j - 1) <= n; i++)
f[i][j] = min(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
for (int i = 1, j, k; i < mid; i++) {
j = 2 * mid - i, k = lcp(i, j);
if (k * 2 - 1 > ans || (k * 2 - 1 == ans && i - k + 1 < St))
ans = k * 2 - 1, St = i - k + 1;
}
for (int i = 2, j, k; i < mid; i++) {
j = 2 * mid - i + 1, k = lcp(i, j);
if (k * 2 > ans || (k * 2 == ans && i - k < St))
ans = k * 2, St = i - k;
}
for (int i = St; i <= St + ans - 1; i++) putchar(a[i]);
}
重复次数最多的连续重复子串
先咕咕了,不会
两个字符串
公共子串
接起来,用 '#' 分隔,求 \(height\) 最大值。
注意判断 \(sa_i\) 和 \(sa_{i-1}\) 应在不同串中
长度不小于 k 的公共子串的个数
经典问题,后缀数组 + 单调栈
首先拼起来,求 \(height\) ,按照 \(k\) 分组。
考虑用每一个 B 串匹配排在它前的 A 串的个数,反过来同理。答案分为两部分
对于同一组每一个 \(A\) 串对每一个 \(B\) 的最大贡献为 \(height-k+1\)
栈记录 \(S\) 和 \(cnt\) 表示当前的 \(height\) 和 \(A\) 串的数量,按照 \(height\) 单增
同时用 \(tot\) 表示当前答案。
若 \(height_i\le S_{top}\) 需要维护:讲 \(tot\) 中 \(cnt\) 个已经累加的 \(S\) 全部替换为当前的 \(height\)
运用了 \(\text{LCP}\) 是区间最小值的特性。
遇到 \(B\) 串,求和。
反过来再算一次。
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long uLL;
typedef long double LD;
typedef long long LL;
typedef double db;
const int N = 200005;
int n, mid, K, m, sa[N], rk[N], id[N], t[N], old[N], h[N], s[N], cnt[N], top;
char a[N];
inline void rs() {
for (int i = 1; i <= m; i++) t[i] = 0;
for (int i = 1; i <= n; i++) ++t[rk[i]];
for (int i = 1; i <= m; i++) t[i] += t[i - 1];
for (int i = n; i >= 1; i--) sa[t[rk[id[i]]]--] = id[i], id[i] = 0;
}
inline int EQ(int x, int y, int k)
{ return old[x] == old[y] && old[x + k] == old[y + k]; }
inline void SA() {
m = 130;
for (int i = 1; i <= n; i++) rk[i] = a[i], id[i] = i;
rs();
for (int k = 1, p; k <= n; k <<= 1) {
p = 0;
for (int i = n - k + 1; i <= n; i++) id[++p] = i;
for (int i = 1; i <= n; i++) if (sa[i] > k) id[++p] = sa[i] - k;
rs(), memcpy(old, rk, sizeof(rk)), p = 0;
for (int i = 1; i <= n; i++) rk[sa[i]] = EQ(sa[i], sa[i - 1], k) ? p : ++p;
if (p == n) break;
m = p;
}
for (int i = 1, j, k = 0; i <= n; h[rk[i++]] = k)
for (k ? k-- : 0, j = sa[rk[i] - 1]; a[i + k] == a[j + k]; k++);
}
int main() {
while (scanf("%d", &K), K) {
scanf("%s", a + 1);
mid = strlen(a + 1);
a[++mid] = '#';
scanf("%s", a + mid + 1);
n = strlen(a + 1);
SA();
top = 0;
LL ans = 0, c = 0, tot = 0;
for (int i = 1; i <= n; i++) {
if (h[i] < K) top = 0, tot = 0;
else {
c = 0;
if (sa[i - 1] < mid) c++, tot += h[i] - K + 1;
while (top && h[i] <= s[top]) {
tot -= cnt[top] * (s[top] - h[i]);
c += cnt[top], --top;
}
s[++top] = h[i], cnt[top] = c;
if (sa[i] > mid) ans += tot;
}
}
top = 0, c = tot = 0;
for (int i = 1; i <= n; i++) {
if (h[i] < K) top = 0, tot = 0;
else {
c = 0;
if (sa[i - 1] > mid) c++, tot += h[i] - K + 1;
while (top && h[i] <= s[top]) {
tot -= cnt[top] * (s[top] - h[i]);
c += cnt[top], --top;
}
s[++top] = h[i], cnt[top] = c;
if (sa[i] < mid) ans += tot;
}
}
printf("%lld\n", ans);
}
}
多个字符串
也是拼起来,用特殊字符分隔。
求出 \(height\) ,二分答案,分组判断。
常见复杂度 \(O(Kn\log n)\) ,其中 \(Kn\) 为 check 复杂度


 浙公网安备 33010602011771号
浙公网安备 33010602011771号