遗传算法案例-货物派送Matlab/Python
对于货物派送问题,白文解释原理,并通过matlab和python分别实现。
问题:
文献:
现有如下30个灾难地点,需要安排车辆去派送物资,现知道车库地点坐标o(35,45),货物仓库地点cage(40,50),
现车库有车56辆,要求分成8个车队(每个车队7辆车,不考虑车的差异,每辆车载重为6,平均车速40)去派送物资,而且时间紧张,每个灾难地点有时间限制。每次装卸物资需要耗时0.5。
要求:
①如果车上物资不够下一个地点使用,回到仓库装满物资再出发
②一个车队要求一起行动,不可分开。
现使用遗传算法求解如何规划使得最优?
L是车队车辆数量,S是车队行驶路程,\(T_超\)是总超时时间,N是超时次数。
python实现
①先导入各种参数。
# 灾难点
ix = [...]
iy = [...]
print(len(ix) == len(iy))
# 灾难点 时间限制和需求货物
ls = [...]
gs = [...]
# 出发点
o = [35, 45]
# 仓库
cage = [40, 50]
c = 30 # 灾难点数量
l = 7 # 车数量
k = 8 # 车队数量
g = 6 # 每辆车载重
v = 40 # 车速
tx = 0.5 # 装卸时间
②做一个简单预处理,将数据整理成数组,并且首先将车辆从车库赶往仓库的时间处理掉。
# 预处理
o_cage = pow(pow(o[0] - cage[0], 2) + pow(o[1] - cage[1], 2), 0.5)
ks = [l * g for i in range(k)]
print(ks)
data = pd.DataFrame(np.array([[i + 1 for i in range(c)], ls, gs, ix, iy]).T, columns=['i', 'ls', 'gs', 'x', 'y'])
# print(data)
sort_data = data.sort_values('ls').values
o_cage_t = o_cage / v
# print(o_cage_t)
sort_data[:, 1] -= o_cage_t
print(sort_data)
③上面我们将所有有用的数据整合成了sort_data一个不规则数组。
下面开始遗传算法
先写一个类 做种群个体初始化和计算适应度
class OneInit:
def __init__(self):
self.ans = None
self.z = 0
self.s = 0
self.all_t = 0
def form_ans(self):
# random.seed(self.seds)
self.ans = [[] for _ in range(k)]
rand_data = random.sample(list(sort_data), c)
for i in range(c): # c 30
self.ans[i % 8].append(rand_data[i])
# sed = random.randint(0, k - 1)
# self.ans[sed].append(list(sort_data[i]))
# for i in self.ans:
# print(i)
def limited(self):
# 初始化一个个体,1/80 得到对应zs
zs = []
for i in range(k):
# 单车队初始
s = 0 # 路程
out_t = 0 # 总超时
all_t = 0 # 时间沙漏
temp_g = l * g
start_p = cage
out_num = 0
# 出仓库
all_t += tx # 装货
for ixx in self.ans[i]:
if temp_g >= ixx[2]:
s1 = self.Edis(start_p, ixx[-2:])
s += s1
all_t += s1 / v
if all_t - ixx[1] > 0:
out_num += 1
out_t += max(0, all_t - ixx[1])
# 卸货
all_t += tx
temp_g -= ixx[2]
start_p = ixx[-2:]
else:
s1 = self.Edis(start_p, cage)
s += s1
all_t += s1 / v
all_t += tx
start_p = cage
temp_g = l * g
zs.append(l * s + out_t * alpha + out_num * beta)
self.s += s
self.all_t += all_t
self.z = sum(zs)
def run(self):
self.form_ans()
self.limited()
@staticmethod
def Edis(x1, x2):
return pow(pow(x1[0] - x2[0], 2) + pow(x1[1] - x2[1], 2), 0.5)
开始建立第一代喽(采用随机的形式建立80个个体,每一个个体是一个问题的解)
我们取出一个个体来看一下他的样子,方便理解
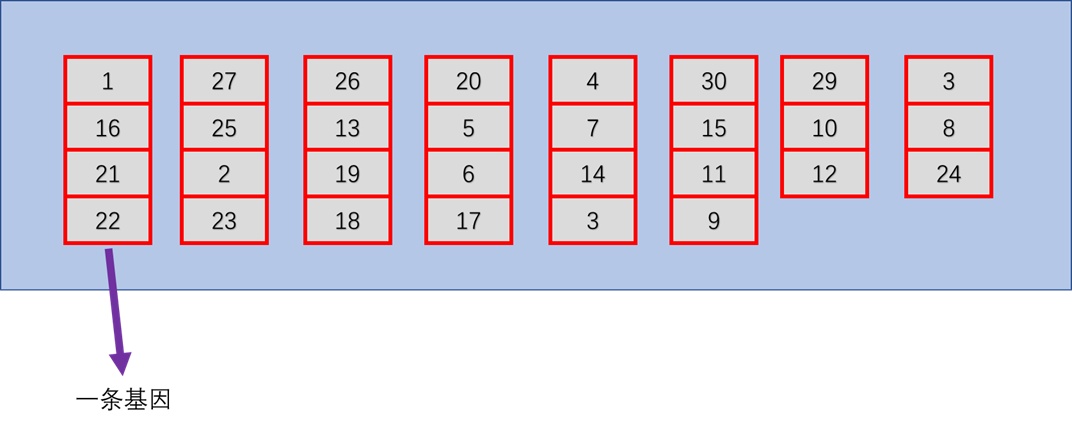
上图表示一个个体,一共8条基因,对应8个车队 一条基因对应车队负责的3或4个点,一开始先这么设置。后面会发生交换和突变 基因中3/4点可能会变,哦不 一定会变的!
第一代,我们先初始化这样的80个个体,就是相当于有了80个随机解,这些解坑定大部分都是垃圾解,但是也有可能有那么一个两个好点的,那么如果让好的解变多,差的解变少呢,哎 达尔文的理论来了,“优胜劣汰“,没错 定义一种惩罚规则 让不好的个体死去,通过个体基因变化产生新个体,如此一代一代变异,淘汰......发展啊发展最终停在某个地方,当然你可以自己设计到底迭代多少次,也可以让机器控制,这里我们手动控制,迭代40次。然后在最新的一代随便拿出一个个体吊打第一代好吧,我们在最新的一代挑一个最健壮的(也就是适应度最高的)拿出来,这个解就是我们问题的解。
过程原理说完了,代码接着往下走
④变异交换和淘汰(交换概率0.8,变异概率0.1)
这里提供两种基因交换思路,一种变异思路
1、自身交换:
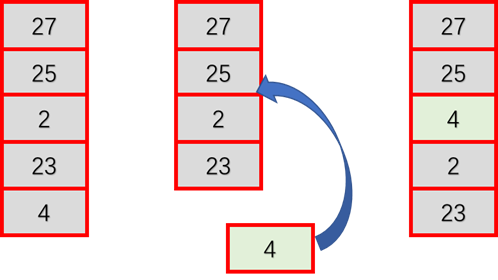
当然这种交换随机的 这里是一个例子,这里是交换了一个,也可以是23号和4号一起断裂,插入到另一个地方。
2、基因间交换
这两种交换都是为了产生更多的解 但是和原种群又不能差别太大,理解这种思路就行,不要问我为什么基因会这样交换!!!问就是为了产生更多相似解,不要问我生物,不要生物,不要...
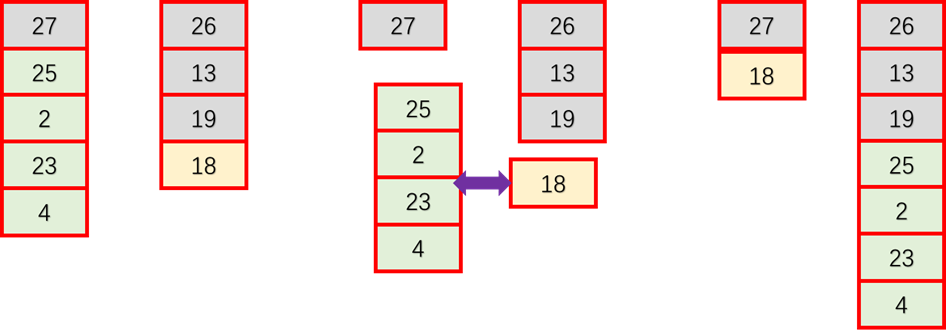
这个例子举的比较极限,但是是真的会发生的。
3、变异
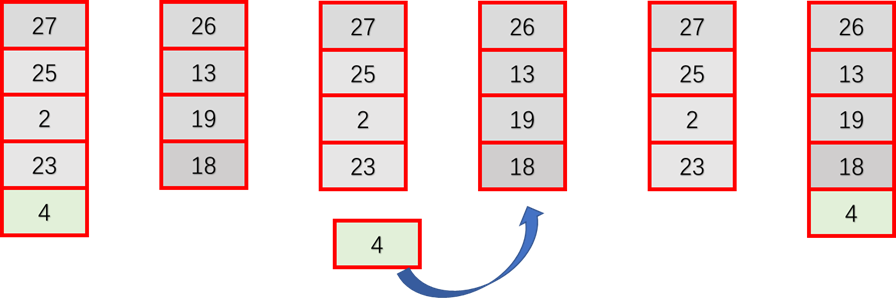
4、淘汰
这里因为进化策略是80个生成80个 就是160个
淘汰法选择局部淘汰:让随机两个个体博弈,适应度低的死,活下来的80个新的(里面可能有上一代旧的)整体应该比上一代要好一些。
MATLAB
其实上面会了改写matlab不是很难,就是要改数据存储形式和一些matlab做不了的小函数要自己写,(吐个槽,为什么要用matlab写遗传算法啊啊啊,没有数组很麻烦)
这里只说一下存储问题,原理就不在说了,代码过几天公开
由于matlab“智”能存储矩阵,所以,要建立一个特别特别大的矩阵(其实并不大,只是数来数去很麻烦)
一个个体
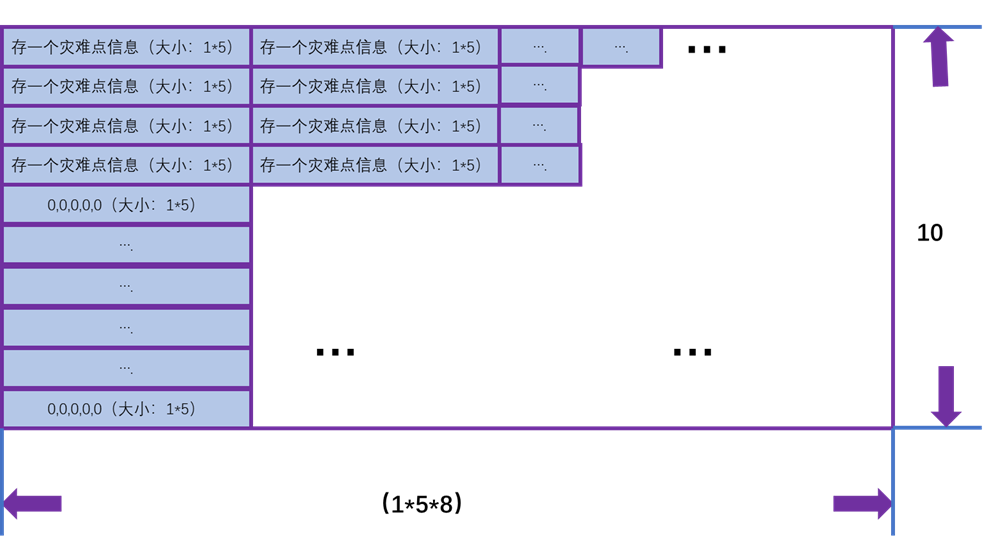
这是一个个体,其实和python是一样的但是由于matlab没有数组不能存放不同大小列表,只能建立一个大一些的,防止溢出。
为什么是1×5×8?
用python展示一下灾难点信息就明了了
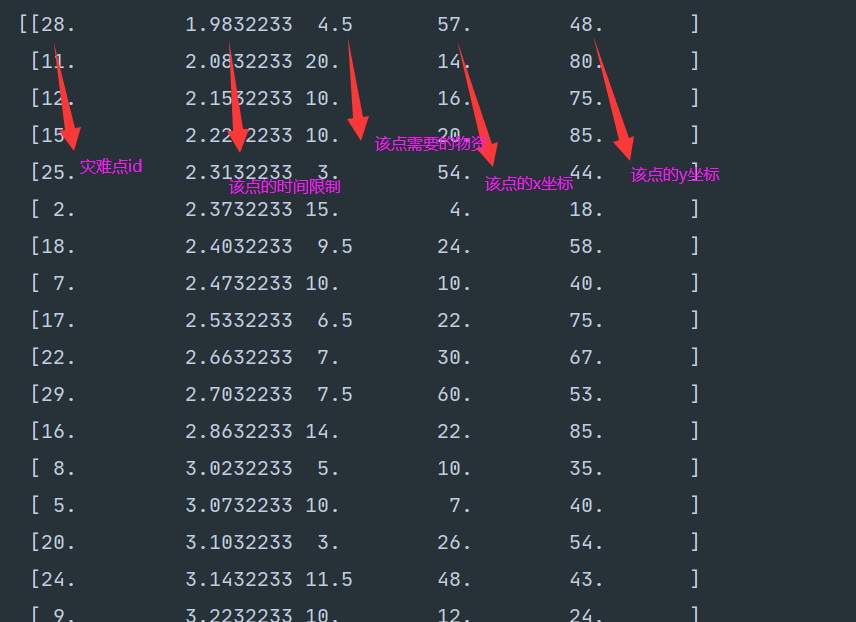
可以发现在上面基因交换变异画的图中 一个带数字的小方块代表的是上图的一行数据。
所以30个点分给8个车队就是这样1×5×8
为什么是10列,不多余吗?
可能多余吧,但是我怕变异,交换的时候某条基因会变特别长,溢出了就麻烦了(看这样实验到最后还是有溢出的,太可怕了)
80个解怎么存储
这个简单,串联就行了 一个个体是1×5×8=40,所以是10×40的大小,一个种群80个所以串联一下最终一个种群的存储矩阵大小为10×(40×80)=10×3200
最后
看一下结果:
python:
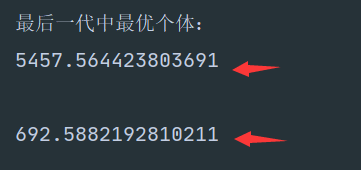
5457这个数应该是越小越好,看的出来python的我写的还不错
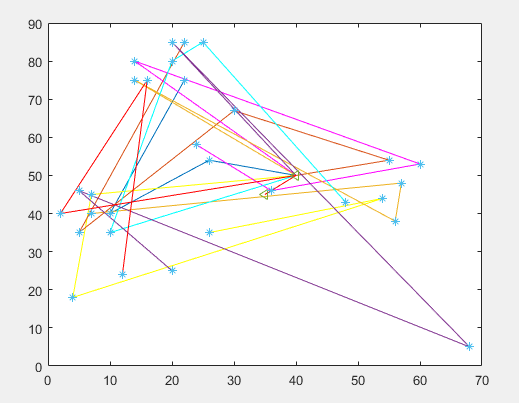
matlab:

对比python 这个就要略高一些,这里是因为基因交换变异那里matlab没有python写的自由。
(这里并不是说matlab做不好,而是对于我来说,不太好写)
python和matlab全部代码见gitee地址如下:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号