聚类学习.4

简单介绍了剩余的评价指标，接上文

关键词：Jaccard系数 FM指数（FMI） Rand指数（RI）DBI DI

介绍篇——评价指标

补充 : 上一篇为针对二分类,如果为三类以上的分类时,对每一类单独分析,即分析A类: A类为正类,其他均为负类,然后按某方法综合分析:
某方法:
1.宏平均（macro）:每一个指标的平均为综合指标。
2.加权平均（weighted）:每一个指标的加权平均为综合指标。
3.微平均（micro）:计算所有类别中假正例、假反例和真正例的总数，然后利用这些计数来计算指标。

外部评价指标分成2部分，1是根据《机器学习》-周志华个人理解，2是资料查阅的（与sklearn库嵌合），两者存在一些差异，如果有知道这是咋回事的欢迎评论区交流。

外部评价指标1

主要介绍三个指标，分别是JC，FMI，RI。

首先，我们有这样一个定义：
对于数据集D = {\(x_1,x_2,x_3...,x_m\)},假定根据某聚类方法得到类簇划分C = {\(c_1,c_2,...c_k\)},参考模型的类簇划分C* = {c*1，c*2，...，c*k}，相应的用 λ 与 λ* 表示C和C*表示的类簇向量：

a = 集合SS: 包含了在C中属于相同簇, 同时在C*中也属于相同簇的样本对数
b = 集合SD: 包含了在C中属于相同簇, 同时在C*中属于不同簇的样本对数        
c = 集合DS: 包含了在C中属于不同簇, 同时在C*中属于相同簇的样本对数  
d = 集合DD: 包含了在C中属于不同簇, 同时在C*中属于不同簇的样本对数

为了更好地理解，举一个例子

聚类类簇划分：[0,0,0,1,1,1]
真实类簇划分：[0,0,1,1,1,0]

根据类簇划分构造两个矩阵：

C（聚类）	0	1	2	3	4	5
0	1	1	1	0	0	0
1	1	1	1	0	0	0
2	1	1	1	0	0	0
3	0	0	0	1	1	1
4	0	0	0	1	1	1
5	0	0	0	1	1	1

C星（真实）	0	1	2	3	4	5
0	1	1	0	0	0	1
1	1	1	0	0	0	1
2	0	0	1	1	1	0
3	0	0	1	1	1	0
4	0	0	1	1	1	0
5	1	1	0	0	0	1

PS：第i行j列个元素表示样本第i个和第j个是否为同一类簇。同则1，否则0.
由于公式要求i<j，所以只用上三角矩阵（加粗の数据）。
a = \(n_{SS}\) = 2
b = \(n_{SD}\) = 4
c = \(n_{DS}\) = 4
d = \(n_{DD}\) = 9
a+b+c+d = m(m-1)/2 = 6×5/2 = 15

Jaccard系数（JC） = a/（a+b+c）
FM指数（FMI） = 根号下（a^2/（（a+b）×（a+c））
Rand指数（RI） = 2（a+d）/（m×（m-1））

以上三个性能区间为 [0,1] ，越大越好.

外部评价指标2

网上查阅得到的做法类似上一篇，先求类似混淆矩阵的矩阵。还是拿上面的例子：

聚类类簇划分：[0,0,0,1,1,1]
真实类簇划分：[0,0,1,1,1,0]

可以得到矩阵如下

C	0	1
0	M00	M01
1	M10	M11

该例子结果：

\[Jaccard = \frac{M_{11}}{M_{01}+M_{10}+M_{11}} \]

内部评价指标

考虑到类簇划分结果为C=\({c_1,c_2,c_3,...,c_k}\)定义：

①簇C内样本间的平均距离：

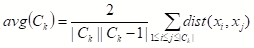
②簇C内样本间的最远距离：

③簇Ci与簇Cj最近样本间的距离

④簇Ci与簇句中心点间的距离

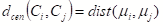
其中dist(x，y)表示x和y的距离，μ表示中心，\(|C_k|\)表示Ck类的个数。

那么评价指标公式为：

DB指数（DBI）：

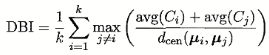
Dunn指数（DI）：

DBI的值越小越好，而DI则相反，值越大越好.

以上是评价指标主要内容，欢迎指正。

询问了下老师，周志华老师的评价系数是针对评价算法本身，而网上的是针对具体数据，应用领域不同。