Codeforces Round #430 (Div. 2)

题目链接：https://codeforces.com/contest/842

A - Kirill And The Game

暴力签到。

B - Gleb And Pizza

题意：有个圆形披萨，圆心在原点，半径为r，且有一个径向长度为d的厚边（crust），然后有一些圆形香肠片，给出他们的半径和圆心。求出有多少个香肠片完全落在厚边内。

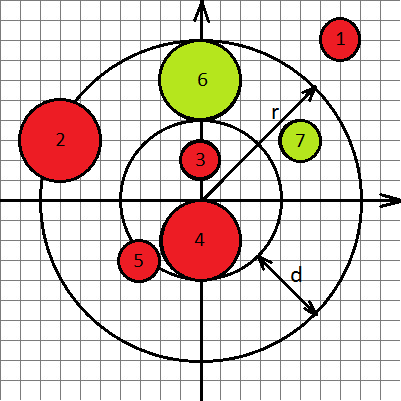
题解：很明显厚边就是一个圆环，求出内径和外径，只要香肠片有某个点在内径以内，就“不是完全落在厚边内”，那肯定也是选这个香肠片离原点最近的点。所以先判断香肠片是否覆盖住原点，否则就可以用香肠片与披萨的圆心距减去香肠片的半径得到最内的点。当然最外的点就很简单，直接用香肠片与披萨的圆心距加上香肠片的半径。假如这两个最极端的点都不在厚边圆环外侧，则其他部分一定在里侧。注意可以通过一系列的平方操作变化这些等式使得最后不需要开方。

设香肠片的圆心离原点的距离为 \(D\) ，香肠片半径为 \(r\) ，厚边圆环的内外径分别为 \(R_1,R_2\) ，则若有

$max(0,D-r)<R_1 $ 或 \(D+r>R_2\) 至少其中之一成立，则计数。其中第一个max去掉也不见得有什么问题。

事实上 \(D\) 不见得是整数，但是由于输入的点都是整数，所以 \(D^2\) 一定是整数，可以变为：

$D^2<(R_1+r)2 $ 或 \(D^2>(R_2-r)^2\) 至少其中之一成立，则计数。

void test_case() {
    int R1, R2, d;
    scanf("%d%d", &R2, &d);
    R1 = R2 - d;
    int n;
    scanf("%d", &n);
    int cnt = 0;
    while(n--) {
        int x, y, r;
        scanf("%d%d%d", &x, &y, &r);
        int D = (x * x + y * y);
        ll Y = R2 * R2 - 2 * R2 * r + r * r;
        if(D > Y)
            continue;
        Y = R1 * R1 + 2 * R1 * r + r * r;
        if(D < Y)
            continue;
        ++cnt;
    }
    printf("%d\n", cnt);
}

C - Ilya And The Tree

题意：给一棵根为1号点的树，每个节点有个权值，权值范围在2e5。对于每个点，都想要最大化1号点到其的路上的所有点的gcd。对于每个点，都可以把一个点的权值变为0，或者不进行修改。注意对上一个点执行完操作后并不会影响到下一个点，也就是大家都是从原本的树上开始修改的。

题解：有个假算法，就是dfs的时候维护修改0次和修改1次的最大的gcd。这个算法假在忽略了gcd并不是越大越好，比如连续向下的三个点9-8-2，这个时候第二个点就应该保留8而不是保留9，这样会使得gcd为2而不是1。想了很久确实不会，看了一下题解。要分把根设为0或者不把根设为0两种情况讨论，第一种情况就是直接dfs下去，第二种情况下，由于gcd中包含根节点，所以一定是根节点的某个因子，由于节点的权值范围不大，枚举根节点的因子，然后确定路上的对这个因子的限制不超过1次，就可以把这一次限制去除。

int a[200005];
int ans[200005];
vector<int> G[200005];

void dfs1(int u, int p, int g) {
    if(p == 0)
        ans[u] = a[u];
    else {
        g = __gcd(g, a[u]);
        ans[u] = g;
    }
    for(auto &v : G[u]) {
        if(v == p)
            continue;
        dfs1(v, u, g);
    }
}

void dfs2(int u, int p, int d, int cnt) {
    if(a[u] % d != 0)
        ++cnt;
    if(cnt <= 1)
        ans[u] = max(ans[u], d);
    else
        return;
    for(auto &v : G[u]) {
        if(v == p)
            continue;
        dfs2(v, u, d, cnt);
    }
}

void test_case() {
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
        scanf("%d", &a[i]);
    for(int i = 1; i <= n - 1; ++i) {
        int u, v;
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    dfs1(1, 0, 0);
    for(int d = 1; d * d <= a[1]; ++d) {
        if(a[1] % d == 0) {
            dfs2(1, 0, d, 0);
            if(d * d != a[1])
                dfs2(1, 0, a[1] / d, 0);
        }
    }
    for(int i = 1; i <= n; ++i)
        printf("%d%c", ans[i], " \n"[i == n]);
}

当cnt>1之后都不能再更新答案，可以直接整个剪掉，略微降低常数。

反思：当时觉得给权值的范围这么小，是有什么特殊用意的，考虑过质因数分解，但是没注意到答案可以在分类讨论之后降低到只有根节点的因子这么多。而且2e5确实可以过n^(3/2)，大概也就1e8这样，常数好一点就可以过。

*D - Vitya and Strange Lesson

题意：有n个非负整数，m次操作，每次操作给所有数字都异或上非负整数x，然后在每次操作之后都输出当前的mex值。mex就是未出现在当前集合中的最小的非负整数。

题解：记得上次camp发现一个规律 \([0+t*2^k,2^k-1+t*2^k]\) 这些区间里面的数，都异或不超过 \(2^k\) 的某个数之后，只是互相交换一下顺序。例如：{0,1,2,3}都异或一个1，得到{1,0,3,2}，{0,1,2,3,4,5,6,7}都异或一个3，得到{3,2,1,0,7,6,5,4}，{0,1,2,3,4,5,6,7}都异或一个6，得到{6,7,4,5,2,3,0,1}，注意假如拿来异或一个16注意假如拿来异或一个8，就不行了。而且很显然不是2的幂的区间也不行，比如[0,9]，2异或9都变成11了。

引发一个思考，是否要把区间断成若干个长度为2的幂的小区间呢？看一下数据范围，暗示我要用线段树？假如建一棵权值树，值域范围是[0,524288)，这是一棵完全二叉树（线段树的梦想？）在每一层线段树的节点，假如x小于一半，则直接往右走（左边子树是不受影响的），否则，把异或x看成两步，先异或一半，交换线段树的两侧子树，然后x就小于一半了。所以操作次数不会超过树高。

实现的时候，可以使用指针连接线段树，然后确实交换两侧子树，也可以打个swp标记在父亲那，但是swp标记会造成查询的时候非常复杂。

const int MAXN = 524288;
bool vis[MAXN + 5];

struct SegmentTree {
    int cnt[(MAXN << 1) + 5];
    int len[(MAXN << 1) + 5];
    int ls[(MAXN << 1) + 5];
    int rs[(MAXN << 1) + 5];
    int lazy[(MAXN << 1) + 5];

    void PushDown(int o, int l, int r) {
        if(lazy[o]) {
            int low = lazy[o] & ((len[o] >> 1) - 1);
            lazy[ls[o]] ^= low;
            lazy[rs[o]] ^= low;
            lazy[o] ^= low;
            if(lazy[o])
                swap(ls[o], rs[o]);
            lazy[o] = 0;
        }
    }

    void Build(int o, int l, int r) {
        if(l == r) {
            cnt[o] = vis[l];
            len[o] = 1;
        } else {
            int m = l + r >> 1;
            ls[o] = o << 1;
            rs[o] = o << 1 | 1;
            Build(ls[o], l, m);
            Build(rs[o], m + 1, r);
            cnt[o] = cnt[ls[o]] + cnt[rs[o]];
            len[o] = len[ls[o]] + len[rs[o]];
        }
        lazy[o] = 0;
    }

    void Update(int x) {
        lazy[1] ^= x;
        return;
    }

    int Mex() {
        int o = 1, curlen = MAXN, res = 0;
        int l = 1, r = MAXN;
        while(curlen > 1) {
            PushDown(o, l, r);
            int m = l + r >> 1;
            if(cnt[ls[o]] == len[ls[o]]) {
                res += len[ls[o]];
                o = rs[o];
                l = m + 1;
            } else {
                o = ls[o];
                r = m;
            }
            curlen >>= 1;
        }
        return res;
    }
} st;

void test_case() {
    int n, m;
    scanf("%d%d", &n, &m);
    for(int i = 1, x; i <= n; ++i) {
        scanf("%d", &x);
        vis[x + 1] = 1;
    }
    st.Build(1, 1, MAXN);
    while(m--) {
        int x;
        scanf("%d", &x);
        st.Update(x);
        printf("%d\n", st.Mex());
    }
}

所以只需要写一个PushDown()和Mex()就做完了。这个PushDown()特别复杂，首先先提取出低位，把低位的值全部下推给lazy，然后再判断高位是否有值，有值则代表要交换两侧区间。Mex()的话，就是在线段树上面找第一个为0的位置。可以记录当前区间的长度（或者左右边界）来确定是否到达递归终点。这里的线段树由于是完全二叉树，所以只需要开两倍空间。

收获：对一个区间一起异或一个数的理解加深了，但是实际上就觉得是很显然的。