2019牛客多校第十场G Road Construction（计算几何）题解

题意：

传送门
给你\(n(n <= 300)\)个点，要求你用一条直线分成数量相同两部分，任意分法都有一个点到直线的最短距离\(d\)，问你\(d\)最大可以是多少。

思路：

先抛出一个结论：这条直线的一定与某两点的连线平行或垂直。
平行时如下图，我分成两部分后为了使\(1\)是部分\(1\)到直线最短的，那我只能让直线和\(1\ 2\)平行，垂直时比如两个点的情况。

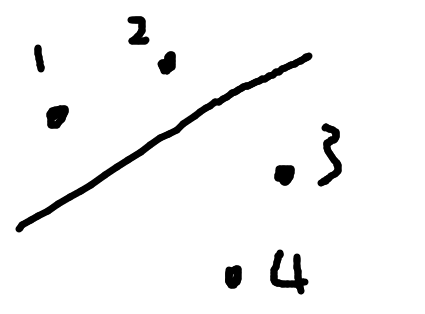
然后我们枚举所有的斜率，把所有点按斜率排序，取中间两个点，让这两个点到直线距离相等，这个距离就是当前的最小距离。然后求最小距离最大值。

代码：

#include<map>
#include<set>
#include<queue>
#include<stack>
#include<ctime>
#include<cmath>
#include<cstdio>
#include<string>
#include<vector>
#include<cstring>
#include<sstream>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 300 + 5;
const int INF = 0x3f3f3f3f;
const ull seed = 131;
const ll MOD = 1e9;
using namespace std;
struct Node{
    double x, y, b;
    bool operator < (const Node &c) const{
        return b < c.b;
    }
}p[maxn];
double x[maxn], y[maxn];
double dis(double k, double b, double x, double y){
    return fabs(k * x + b - y) / sqrt(k * k + 1.0);
}
int main(){
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%lf%lf", &x[i], &y[i]);
        p[i].x = x[i], p[i].y = y[i];
    }
    double ans = 0;
    for(int i = 1; i <= n; i++){
        for(int j = i + 1; j <= n; j++){
            double k = (y[i] - y[j]) / (x[i] - x[j]);
            for(int h = 1; h <= n; h++){
                p[h].b = p[h].y - k * p[h].x;
            }
            sort(p + 1, p + n + 1);
            double b = (p[n / 2].b + p[n / 2 + 1].b) / 2.0;
            ans = max(ans, dis(k, b, p[n / 2].x, p[n / 2].y));

            k = -1.0 / k;
            for(int h = 1; h <= n; h++){
                p[h].b = p[h].y - k * p[h].x;
            }
            sort(p + 1, p + n + 1);
            b = (p[n / 2].b + p[n / 2 + 1].b) / 2.0;
            ans = max(ans, dis(k, b, p[n / 2].x, p[n / 2].y));
        }
    }
    printf("%.10f\n", ans);
    return 0;
}