24.12.26

因为明天放假所以今天加赛这件事

A

NT 一眼看出历史和，然后发现历史和是等差数列求和直接秒了。
我的探索历程就很莫名其妙了。

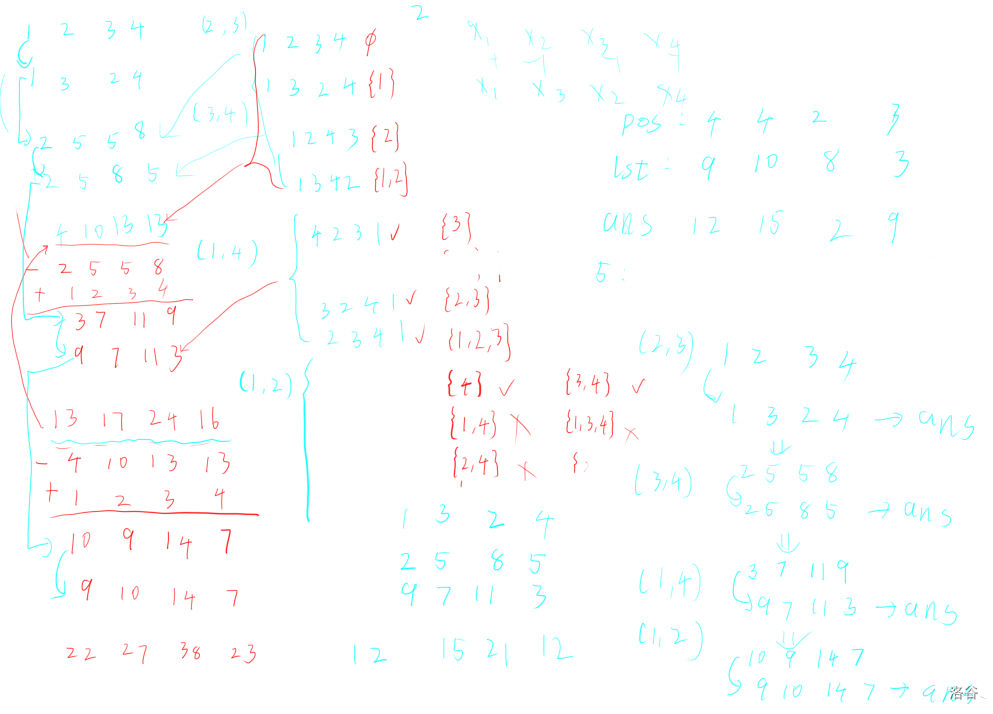
首先注意到可以时刻维护当前所有情况的和。
然后一次操作直接把对应位置交换加到求和数组里。

但是这种情况会统计到一些多余情况，example：

                        是经历了哪些操作的序列的和
 1  2  3  4 
  swap(2, 3)
 1  3  2  4
  plus
 2  5  5  8          <- [{0}, {1}]
  swap(3, 4)
 2  5  8  5          <- [{2}, {1, 2}]
  plus
 4 10 13 13          <- [{0}, {1}, {2}, {1, 2}]
  swap(1, 4)
13 10 13 4           <- [{3}, {1, 3}, {2, 3}, {1, 2, 3}]
  plus                        ------
17 20 26 17          <- [自己看]

这样就会出现不合法情况，那么这个不合法情况是从 2 5 5 8 的 [{1}] 中转移来的
考虑直接减去

...

   4 10 13 13
 - 2  5  5  8
 + 1  2  3  4
 = 3  7 11  9
    swap(1, 4)
   9  7 11  3

但是又减又加的怎么维护，发现减完其实是 2 5 8 5，那么把所有流程可以改写成这样。

   1  2  3  4
  swap(2, 3)
   1  3  2  4    -> add to ans
 + 1  2  3  4
   2  5  5  8
  swap(3, 4)
   2  5  8  5    -> add to ans
 + 1  2  3  4
   3  7 11  9
  swap(1, 4)
   9  7 11  3    -> add to ans

最后答案就是交换完的这些位置求和。

然后注意到每次是对 \(a_i \gets a_i + i\)。
所以只有每次交换的位置有大变化，剩下在进行等差数列的变化，所以记录每个位置上一次变化是什么时候，在交换和最后时对其等差数列求和统计进答案即可。

B

说的很好，让我调了一下午。
没什么好说的，调整法我也不会用，贪心也不会证，所以直接选择相信它开码。

调了一下午的线段树二分：

LL d[N];
int Max(int x, int y) {return d[x] > d[y] ? x : y;}
// ...

// dmx 维护最大 d 的下标，mx 维护最大的 sum
PLI find(int ll, int rr, LL Lmx, int l = 1, int r = n, int rt = 1) {
	if (l == r) return PLI(max(Lmx, t[rt].mx) - d[t[rt].dmx], t[rt].dmx);
	pushdown(rt);
	if (rr <= mid) return find(ll, rr, Lmx, l, mid, lrt);
	int Rid = Max(mid, t[rrt].dmx);
	LL vL = max(Lmx, t[lrt].mx), vR = t[rrt].mx, dR = d[Rid];
	if (vL - dR < vR) {
		PLI res = find(ll, rr, vL, mid + 1, r, rrt);
		return min(PLI(vR, Rid), res);
	} else {
		PLI res = find(ll, rr, Lmx, l, mid, lrt);
		return min(PLI(vL - dR, Rid), PLI(max(res.fi, vR), res.se));
	}
}

C

不会

---

HE 8 个队。

...