24.12.24

好像用了快一天看了看这辈子也用不到的东西呢。
感觉在场上不如直接暴力呢。

---

插头 dp
轮廓线 dp

网格图状压 dp 的一种方式，即逐格 dp。
以我的脑子只会限制四联通下的轮廓线。
限制跨了多行还是压整行逐行 dp 罢。

轮廓线：已决策状态和未决策状态的分界线

压的（应该）是已决策状态对未决策状态的限制。

可能长这两样

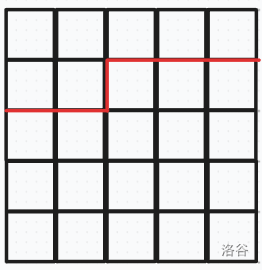
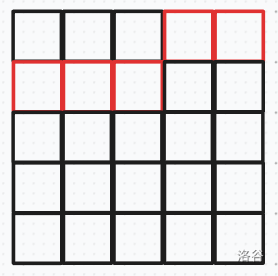
那么在逐格转移时一个格子只受上面和左侧的已决策部分的限制，对右侧和下面的未决策部分造成限制，对状态与它无关的部分不动，单次转移复杂度 \(O(1)\)。

一般逐格转移复杂度 \(O(n^2Base^n)\)，暴力枚举相邻两行状态转移复杂度 \(O(n \cdot Base^{2n})\)，所以这个复杂度似乎要优一点。

---

插头：一个格子某个方向的插头存在，表示这个格子在这个方向与相邻格子相连。

这个术语似乎更针对一条线的那种轮廓线。

有插头就说明那个格子的路径一定要扩展到对应方向的格子，如果这个方向有障碍 / 超出边界 / 两个插头撞一块了并且依据题意不能相连，那么说明状态非法。

---

对于要求找（一条/若干条）路径 / 回路使用线形的轮廓线（因为一个格子只能选一个方向出去）。
对于连通块使用块形的轮廓线（四个方向都会联通）。

对于不要求选出的路径 / 回路条数为 1 的题目轮廓线可以只记录轮廓线上插头的存在性。
如果要求条数为 1 需要记录插头的连通性。

• 括号表示：路径模型都适用吧，由于不连通的两条线一定不交，同一连通块在轮廓线上一定有两个端点，所以轮廓线上的插头匹配情况一定是括号匹配。
• 最小表示：更普适一点，连通性相同的插头用同一编号表示，然后最后处理状态保持最小表示（从左到右扫，第一次出现的重编号为 1，第二次出现的重编号为 2，以此类推）。

括号表示是三进制状压（空，左括号，右括号），最小表示需要的编号最大为 \(\left\lceil \frac{m}{2}\right\rceil\)（染色模型的最极端情况）。
就状态存储来说括号表示是要优一些的。

---

一般都是要滚动数组的吧。

---

对于需要记录连通性的轮廓线，一般能用括号表示用括号表示，用不了用最小表示。
用括号表示是三进制状压，用最小表示是 * 进制状压，如果为了方便使用位运算可以补到 2 的整次幂进制。

---

对于括号表示，压的是括号序列，对于最小表示，以四联通为例，那么两个位置想在不同连通块至少要隔一个空位。总之就是，有很多状态都是非法状态，但是把需要表示的状态搞得值域很大，可以使用哈希表记录那些合法状态的 dp 值，额外用 vector 什么的存一下当前的合法状态。

特别的，如果用 unordered_map，gp_hash_table，cc_hash_table 等 STL 自带的哈希表，可以用

for (auto [states, val] : dp)

遍历哈希表，那么不用额外用 vector 记录状态了。

特别的，上述三种哈希表的表现优劣排序在不同题中为乱序，在较多数 (?) 情况下可能有 cc_hash_table 优于 unordered_map &^=*_$ gp_hash_table。

记录合法状态这种优化对于那些只需记录存在性的轮廓线也可以用，那个的 dp 值直接用数组存就好了。

---

对于线形的轮廓线在换行时需要注意的点：

---

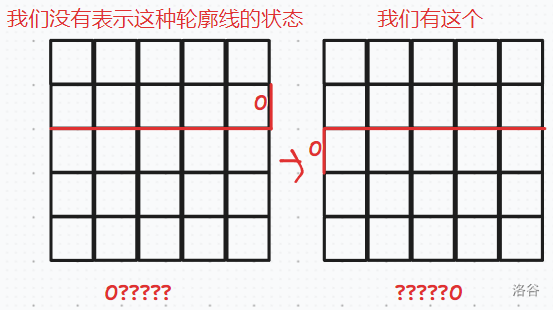
上面的一些
对于插头 dp 来说
还是比较普适的（……吧？）
这个玩意比较恶心的一点在于对于不同的题转移需要的分讨是不同的。
并且量可能有些大。
并且细节可能有些多。

哦，比较模板的分讨就考虑转移一个格子会受到上左两插头限制，会生成右下两插头，分上左两插头分别是啥去讨论。
注意转移的不重不漏。

---

P5074

若干回路的铺线，只记录存在性。
如果不能铺，要求上左插头都是 0。
如果上左插头都是 0，新建右下插头都是 1。
如果只有一个是 1，新的右下插头也只有一个是 1。
如果都是 1，那么两条线合并，右下插头都是 0。

P5056

宇宙万法的那个源头，不知道是不是这道题。

if (!mp[i][j]) {
	// 不能铺 要求上左插头是 `0`
	if (!lt && !up) f[op][sta] += v;
} else if (!lt && !up) {
	// 上左是 `0` 新建连通块 要求右下可达
	if (!mp[i + 1][j] || !mp[i][j + 1]) continue;
	f[op][sta ^ (1 << l) ^ (2 << u)] += v;
} else if (!lt && up) {
	// 有一侧有插头 选择一个方向延申该插头 要求对应方向可达
	if (mp[i][j + 1]) f[op][sta] += v;
	if (mp[i + 1][j]) f[op][sta ^ (up << l) ^ (up << u)] += v;
} else if (lt && !up) {
	// 有一侧有插头 选择一个方向延申该插头 要求对应方向可达
	if (mp[i + 1][j]) f[op][sta] += v;
	if (mp[i][j + 1]) f[op][sta ^ (lt << l) ^ (lt << u)] += v;
} else if (lt == 1 && up == 1) {
	// 合并左括号 找到对应的第一个右括号改成左括号
	for (int k = l + 4, cnt = 1; k < m * 2; k += 2) {
		if ((sta >> k & 3) == 1) ++cnt;
		if ((sta >> k & 3) == 2) --cnt;
		if (!cnt) {
			int nxt = sta ^ (1 << l) ^ (1 << u) ^ (3 << k);
			f[op][nxt] += v; break;
		}
	}
} else if (lt == 2 && up == 2) {
	// 合并右括号 找到对应的第一个左括号改成右括号
	for (int k = l - 2, cnt = 1; k >= 0; k -= 2) {
		if ((sta >> k & 3) == 2) ++cnt;
		if ((sta >> k & 3) == 1) --cnt;
		if (!cnt) {
			int nxt = sta ^ (2 << l) ^ (2 << u) ^ (3 << k);
			f[op][nxt] += v; break;
		}
	}
} else if (lt == 2 && up == 1) {
	// 合并 右括号 和 左括号  直接合并
	f[op][sta ^ (lt << l) ^ (up << u)] += v;
} else if (lt == 1 && up == 2) {
	// 合并 左括号 和 右括号  说明产生闭合回路 要求只在最后铺线格合并
	if (i == Ex && j == Ey) ans += v;
}

P2289 [HNOI2004] 邮递员：__int128 版双倍经验，因为能正着走一遍反着走一遍最后答案乘 2。
那么在 08 年 cdq 论文出来前这个咋写？

P3272

考虑 L 形地板硬要说的话可以是 L 形路径。
限制是路径只能拐一个弯。

若干个地板只需记录存在性。
把只能拐一个弯的限制放到状态里，记没拐过弯的插头为 1，拐过弯的插头为 2。

二元组 (左, 上) -> (下, 右)：

(0, 0): 新建 (0, 1) 或 (1, 0) 或 (2, 2)
(1, 0): 延申 (0, 1) 或 拐弯 (2, 0)
(0, 1): 延申 (1, 0) 或 拐弯 (0, 2)
(1, 1): 链接 后面走不了了 (0, 0)
(2, 0): 延申 (0, 2) 或 止步于此 (0, 0)
(0, 2): 延申 (2, 0) 或 止步于此 (0, 0)
剩下的状态非法
所有将要延申方向都要求能延申（不出界，非障碍）

另
本题中 cc_hash_table 以 567ms(总) 一骑绝尘
unordered_map 取得 1.35s(总) 成绩
gp_hash_table 80pts

P4262

骨牌覆盖 经典轮廓线 dp

(zuo, shang) -> (xia, you)：

(0, 0): 往下放 (1, 0) 往右放 (0, 1)
(0, 1): 被放了 (0, 0)
(1, 0): 被放了 (0, 0)
(1, 1): 非法

要求能延伸

然后枚举哪个格子是障碍可以 \(O(n^2m^22^m)\) 豪取（可能）33pts 的好成绩。

我们考虑正着跑一遍倒着跑一遍那么对于一个格子它将会被两条轮廓线包起来：

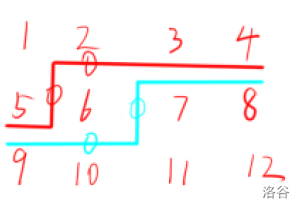
如果两条轮廓线在当前格子周围的两个状态都是 0，并且剩下的状态分别对齐，那么两条轮廓线就可以拼出当前格子为障碍的一种局面，对当前格子的贡献就是两边乘法原理乘起来。