简单易懂的博弈论讲解(巴什博弈、尼姆博弈、威佐夫博弈、斐波那契博弈、SG定理)
博弈论入门:
巴什博弈:
两个顶尖聪明的人在玩游戏,有一堆$n$个石子,每次每个人能取$[1,m]$个石子,不能拿的人输,请问先手与后手谁必败?
我们分类讨论一下这个问题:
当$n\le m$时,这时先手的人可以一次取走所有的;
当$n=m+1$时,这时先手无论取走多少个,后手的人都能取走剩下所有的;
当$n=k*(m+1)$时,对于每$m+1$个石子,先手取$i$个,后手一定能将剩下的$(m+1-i)$个都取走,因此后手必胜;
当$n=k*(m+1)+x(0<x<m+1)$时,先手可以先取$x$个,之后的局势就回到了上一种情况,无论后手取多少个,先手都能取走$m+1$个中剩下的,因此先手必胜。
结论:
通过上面的分析可以得出结论:当$n$能整除$m+1$时先手必败,否则先手必胜。
尼姆博弈(Nim):
两个顶尖聪明的人在玩游戏,有$n$堆石子,第$i$堆有$a_{i}$个,每人每次能从一堆石子中取任意多个石子但不能不取,不能拿的人输,请问先手与后手谁必胜?
我们从简单的情况入手:
当$n=1$时,显然先手取走这一堆就能获胜;
当$n=2$且$a_{1}!=a_{2}$时,我们假设$a_{1}>a_{2}$,先手可以先在第一堆取走$a_{1}-a_{2}$个,下一次无论后手取走多少个,先手都可以在另一堆取走同样多个,因此先手必胜;
当$n=2$且$a_{1}==a_{2}$时,先手无论取走多少个,后手都能在另一堆取走同样多个,因此后手必胜。
当$3\le n$时呢?
问题变得繁琐起来,这时就要一个有规律性的结论。
结论:
当$a_{1}$^$a_{2}$^$……$^$a_{n}=0$时先手必败,反之先手必胜。
为什么这个结论是对的?
假设当前异或和为$0$,这时先手在某一堆取走了若干个,局势变成了$a_{1}$^$a_{2}$^$……$^$a_{i}'$^$……$^$a_{n}=k$,也就是$a_{1}$^$a_{2}$^$……$^$a_{i}'$^$……$^$a{n}$^$k=0$。
假设$k$的最高位$1$在第$x$位,那么一定有一个数$a_{j}$使得$a_{j}$的第$x$位为$1$。
那么我们只要能将$a_{j}$变成$a_{j}$^$k$,就能使异或和又等于$0$,后手一直这样取,最后$a_{1}=a_{2}=……=a_{n}=0$时,异或和是$0$,这时先手无法取了,先手就一定必败了。
那么能否每次都将$a_{j}$变成$a_{j}$^$k$呢?
答案是可以的,因为aj比k多出的高位异或后不变,第$x$位异或后为$0$,无论低位是什么,在第$x$位变$0$后整个数都会变小。
也就是说$a_{j}$^$k$一定小于$a_{j}$,那么后手每次只要在第$j$堆取走$a_{j}-(a_{j}$^$k)$个石子就好了。
EX:nimk游戏
如果将游戏改成每人每次可以从$[1,d]$堆中各取任意多个石子呢?
这个游戏实际是$nim$游戏的扩展版,也有一个很好的结论:将每堆石子数用二进制表示,对于二进制的任意一位,如果这一位为$1$的石子堆数$\%(d+1)$都得$0$,那么先手必败,否则先手必胜。
证明的话与$nim$游戏类似,我们只需要证明三点:
1、终止局面为先手必败(显然)
2、任意先手必胜的局面都能传变成先手必败的局面。
3、任意先手必败的局面都不能转变为先手必胜的局面。
先来证明第$2$个:假设最高一位$\%(d+1)$不得$0$的位有$m$个$1$,那么将这些堆的这一位变成$0$;假设下一个$\%(d+1)$不得$0$的位有$n$个,之前那$m$堆中这一位有$a$个$1$和$b$个$0$。如果$n\le a$,显然将这$a$个中$n$个变成$0$即可;如果$(d+1)-n\le b$,那么只要将$b$个中的$(d+1)-n$个变成$1$即可,因为之前最高位是将$1$变$0$,所以这一位即使由$0$变$1$,这堆石子数也是减少的;如果这两个都不满足,那么$a<n\&\&b<(d+1)-n$,这时只要将这$a$堆和这$m$堆之外的$n-a$堆的这一位$1$变成$0$,那么总改变堆数为$a+b+(n-a)=b+n<(d+1)-n+n=d+1$,也就是说将这一位变为$\%(d+1)=0$需要改变的总堆数要小于$(d+1)$,即可以一次操作完成,然后以此类推就能使每一位都变为$\%(d+1)=0$。
再证明第$3$个:因为一次最多操作$d$堆石子,因此不能将$(d+1)$堆某一位是$1$的石子堆的这一位都变为$0$。
威佐夫博弈:
两个顶尖聪明的人在玩游戏,有2堆石子,每人每次可以拿走任意一堆中任意数量的石子或在两堆石子中拿走相同数量的石子,不能拿的人输,请问先手与后手谁必胜?
威佐夫博弈不同于尼姆博弈和巴什博弈,它不能将两堆石子分开来分析,但它也有一个规律性的结论。
我们定义先手必败的局势为奇异局势,那么前几个奇异局势分别为:
$(0,0),(1,2),(3,5),(4,7),(6,10)……$
那么奇异局势有什么性质呢?
对于第$k$个($k$从$0$开始)奇异局势$(x,y)$,$x$为前$0\sim k-1$个奇异局势中没有出现过的最小自然数,$y=x+k$。
我们将这些奇异局势在平面直角坐标系上画出来:

我们可以将两堆石子看成是棋盘上一个点的横纵坐标,那么游戏就变成了:棋盘上有一个点,每次每人只能将棋子往左或往下移动任意个格子或往左下移动任意个格子,不能移动的人输。终止节点显然是$(0,0)$,我们将能一步到达$(0,0)$的点都染色,那么这些点就都是必胜态,再找到横纵坐标之和最小的没被染色的点,这个点就是下一个必败态,由此就能画出上图。
可以看出任意一个自然数包含在一个且仅有一个奇异局势中(默认$x<y$)。
那么怎么求一个局势是否为奇异局势呢?
根据Betty定理,第$k$个奇异局势就是$\left (\left \lfloor \frac{1+\sqrt{5}}{2}k \right \rfloor,\left \lfloor \frac{3+\sqrt{5}}{2}k \right \rfloor \right )$,因为$k=y-x$,只要将$k$带入后判断求得的$x,y$是否是输入的$x,y$即可。
EX:扩展威佐夫博弈
按照上面在棋盘上移动棋子的方式,每次向左下移动可以看作是向左移动$dx$,向下移动$dy$,要求$|dx-dy|<1$。那么如果将这个要求扩展到$|dx-dy|<d$呢?我们同样可以得出第$k$个奇异局势$(x,y)$,$x$为前$0\sim k-1$个奇异局势中没有出现过的最小自然数,$y=x+d*k$。根据$Betty$定理同样能得出第$k$个奇异局势为$\left ( \left \lfloor \frac{2-d+\sqrt{d^2+4}}{2} k \right \rfloor,\left \lfloor \frac{2+d+\sqrt{d^2+4}}{2}k \right \rfloor \right )$。
斐波那契博弈:
两个顶尖聪明的人在玩游戏,有一堆石子,先手第一次可以拿任意多个但不能全拿走也不能不拿,之后每个人最少拿一个,最多拿前一个人两倍那么多个,谁取到最后一个谁就能获胜,请问先手后手谁必胜?
看到博弈的名字大概就已经能猜到结论是什么了吧?
没错,结论就是当石子数为斐波那契数时先手必败,反之先手必胜。
证明:
我们可以用数学归纳法来证明。
设石子数n为$f[i]$(斐波那契数列第i项)
当$i=2$时,$n=2$,显然先手只能取一个,后手必胜。
当$i>2$时,假设我们已经证明$n=f[i-1]$时的结论是成立的,那么$f[i]=f[i-1]+f[i-2]$。
我们将这一堆石子分成$f[i-1]$和$f[i-2]$两部分来看。
假设先手第一次取$x$个,后手第一次取$y$个。
如果$x<\frac{f[i-2]}{3}$,因为$n=f[i-2]$时已经证明后手一定能取到$f[i-2]$个中的最后一个,所以问题转化成了有$f[i-1]$个石子,谁能取到最后一个,这个也已经证明后手必胜,所以当$x<\frac{f[i-2]}{3}$时,后手必胜。
如果$x>=\frac{f[i-2]}{3}$且$x\le f[i-1]$,则这$f[i-2]$个中剩余的小于$2x$个,后手可以直接取完,那么后手取了$f[i-2]-x$个,即$y\le\frac{2f[i-2]}{3}$。我们比较一下$\frac{2f[i-2]}{3}$与$\frac{f[i-1]}{2}$的大小即比较$4*f[i-2]$与$3*f[i-1]$的大小。因为$3*f[i-3]>2*f[i-3]>f[i-2]$,所以$3*f[i-3]+3*f[i-2]>4*f[i-2]$即$3*f[i-1]>4*f[i-2]$,也就是说在后手取完$f[i-2]$那一堆石子后,先手不能取完剩下的$f[i-1]$个石子,问题就有变成了有$f[i-1]$个石子时的情况。
如果$x>f[i-2]$,因为$f[i-1]<2*f[i-2]$,所以后手能取走剩下所有的。
综上三种情况可以推知,当$n=f[i-1]$时结论成立,那么$n=f[i]$时结论必然成立。
阶梯博弈:
阶梯博弈并不是一种具体的博弈问题,而是一类博弈问题的变形。
就拿阶梯尼姆博弈举例:
两个绝顶聪明的人在玩游戏,有$n$堆石子,每次每人可以取走第$i$堆($i>1$)任意数量的石子并将它们放到第$i-1$堆,或者直接取走第一堆的任意数量石子,不能操作的人输,请问先手能否必胜?
对于这一类问题我们将堆的编号分奇偶考虑,如果只有奇数编号那些堆石子,这就是一个尼姆博弈。现在加入了偶数编号的堆,同样不影响答案,因为如果有人将偶数编号第i堆的石子移到第$i-1$堆,那么另一个人可以将上一个人操作的那些石子从第$i-1$堆再移到第$i-2$堆,这样奇数编号堆的局势没变,两人的先后手关系也没变,相当于将偶数堆编号的石子往前移了两次。而移动奇数堆到偶数堆就相当于拿走了石子。
那么为什么选择将奇数堆看做尼姆博弈而不是偶数堆呢?
因为虽然偶数堆做尼姆博弈也是相当于拿走石子,但最后石子会堆在第一堆,我们无法判断哪个人会在什么时候清空第一堆的石子。
组合游戏:
讲了这么久,我们所说的博弈问题到底是什么样的?我们要研究的又是什么样的问题呢?
我们研究的是一类游戏,叫平等组合游戏($ICG$)
那么什么样的游戏可以被称为$ICG$呢?
1、两个人进行博弈
2、两人轮流进行决策且做出的决策都对自己有利
3、游戏中同一个局势不能多次到达且游戏不能有平局
4、当有人无法做出决策时游戏结束,无法做出决策的人输
5、游戏可以在有限步数内结束
6、任意游戏者在某一局势时能做出决策的集合只与当前局势有关,与游戏者本身无关
必胜态与必败态:
定义$P-position$与$N-position$
$P-position$:必败态(简称$P$),即在决策前就处于这种状态的人必败
$N-position$:必胜态(简称$N$),即在决策前就处于这种状态的人必胜
如果更严谨的定义$P$与$N$,则:
1、无法移动的状态为$P$
2、可以移动到$P$的状态为$N$
3、任意移动都会到$N$的状态为$P$
组合游戏的DAG图:
如果我们将每一种状态向它能到达的状态连边,那么一个组合游戏的所有状态就能组成一个$DAG$(有向无环图)。
给出一张DAG,在给定起点处有一枚棋子,两人轮流移动棋子,如果谁不能移动了就判输。
事实上,所有的$ICG$问题都可以抽象成上述的这个游戏。
SG函数及SG定理
$SG$函数是人们在研究博弈问题上迈出的一大步,人们不再一味的通过找规律来得到博弈结论,而是将博弈问题的每一个状态进行量化分析并总结出了某些普遍性的规律。
首先定义$mex$运算,表示集合中最小的没出现过的自然数,例如:$mex\{1,2,3\}=0$,$mex\{0,2,3\}=1$,$mex\{0,1,2\}=3$
$SG$函数描述的是博弈中某个状态量化后的值,$SG(x)=mex\{SG(y)|x\ can\ go\ to\ y\}$
我们来分析一下$SG$函数的性质:
1、终止状态$SG$值为$0$,因为它没有出边(即可到达的状态)
2、$SG$值为$0$的状态为必败态,它的后继状态$SG$值都不为$0$,满足必败态定义
3、SG值不为$0$的状态为必胜态,它的后继状态$SG$值有为$0$的状态,满足必胜态定义
由此我们知道了对于尼姆博弈每一堆石子的$SG$值就是这堆的石子数,而尼姆博弈的判断方式是每堆石子数的异或和是否为$0$,也就是每堆石子$SG$值的异或和是否为$0$。那么其他组合游戏是否也能同这个结论来判断呢?答案是可以的,这就是$SG$定理。
SG定理:游戏的和为每个单一游戏SG值的异或和。
单一游戏就是原游戏的子游戏,例如尼姆博弈中的一堆石子。
那么一个局面为先手必败当且仅当该局面的$SG$值为$0$。同样如果游戏的和为$0$,那么先手必败。
这个证明和尼姆博弈的证明类似:
所有终止状态的$SG$值都是$0$,每次如果先手使本来$SG$值异或和为$0$的局面异或和改变为$k$,那么后手就一定能找到一个单一游戏使它的$SG$值从$SG(x)$变成$SG(x)$^$k$。因为$SG(x)$^$k<SG(x)$,而$x$的后继状态一定有一个状态的$SG$值为比它小的$SG(x)$^$k$。
那么$SG$函数怎么求?
按照定义,依次枚举每种状态并枚举每种状态能到达的状态,找到每个状态后继状态$SG$值中没有出现的最小自然数就是它的$SG$值。
anti-SG与SJ定理
$anti-SG$组合游戏的其他规则与$SG$组合游戏规则相同,但它规定决策集合为空者获胜。
我们先来看看anti-尼姆博弈:
两个顶尖聪明的人在玩游戏,有$n$堆石子,第$i$堆有$a_{i}$个,每人每次能从一堆石子中取任意多个石子但不能不取,取到最后一个的人输,请问先手与后手谁必胜?
经过分析,我们发现先手必胜有两种情况:
1、每堆石子数异或和不为$0$且至少有一堆石子数大于$1$
2、每堆石子数异或和为$0$且每堆石子只有$1$个
对于第二种情况显然是对的,但第一种为什么就能先手必胜呢?
我们先除去偶数堆石子数为$1$的石子堆(因为这些一定是轮番取完且不改变先后手关系),先手只要第一次取石子使剩下石子堆异或和为$0$,之后每次只要后手改变异或值就将异或值再取为$0$,到最后一定会剩下两堆同样多数目且数目都大于$1$的石子,假设每一堆剩下$1+x$个石子($x>0$),这时后手先取:
如果后手将一堆全取走,那么先手将另一堆取$x$个即可,这时只剩下$1$个;
如果后手使一堆剩下$1$个,那么先手将另一堆全取走即可,这时只剩下$1$个;
如果后手使一堆剩下大于$1$个,那么先手在另一堆取同样多个,局势又变成了剩下两堆$1+x$个石子的情况。
那么能否将anti-尼姆博弈也推广成$anti-SG$组合游戏呢?
当然是可以的,这就是$SJ$定理:
对于anti-SG游戏,先手必胜当且仅当:
1、游戏的和不为0且至少有一个单一游戏的SG函数大于1
2、游戏的和为0且所有单一游戏的SG函数不大于1
证明和上面$anti-Nim$的证明相同,只不过对于第二种情况一个$SG$函数为$1$的局势可以变成$SG$函数大于$1$的局势,只要将这种情况转为第一种情况就好了。
multi-SG
$multi-SG$游戏的规则与$SG$游戏相同但多出一个可以将单一游戏分成多个单一游戏的操作。对于分裂单一游戏的操作,分裂后的状态的$SG$值可以看做是分裂出的单一游戏$SG$值的异或和。
我们来看一下$multi-Nim$游戏:
有$n$堆石子,两个人可以从任意一堆石子中拿任意多个石子(不能不拿)或把一堆数量不少于2的石子分为两堆不为空的石子。
规定没法拿的人失败,问谁会胜利?
我们手动求一下前几个状态的$SG$值:
$sg(1)=mex\{sg(0)\}$
$sg(2)=mex\{sg(0),sg(1)\}=2$
$sg(3)=mex\{sg(0),sg(1),sg(2),sg(1,2)\}=4$
$sg(4)=mex\{sg(0),sg(1),sg(2),sg(1,3),sg(2,2),sg(3)\}=3$
如果继续推下去可以发现一个结论:
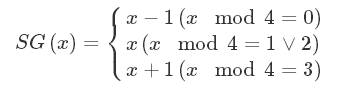
every-SG
$every-SG$游戏规定对于任意未结束的单一游戏,游戏者必须对它进行决策,游戏结束时间决定于最后一个结束的单一游戏,胜负则取决于最后一个结束的单一游戏的输赢。
对于每一步决策,因为一直$SG$值为$0$时必败,$SG$值不为$0$时必胜,所以我们一定希望$SG$为$0$的局势尽快结束,$SG$不为$0$的局势尽量慢点结束。
所以需要知道$SG$值为$0$的局势最少多少步结束,$SG$值不为$0$的局势最多多少步结束。
我们用$step$函数来记录这个值:
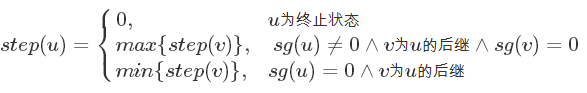


 浙公网安备 33010602011771号
浙公网安备 33010602011771号