DS博客作业03--树
0.PTA得分截图

1.本周学习总结
1.1 总结树及串内容
- 串的BF\KMP算法
-
串的BF算法:简单点说,BF算法就是将子串中的字符与主串中的字符一一进行比对,如果出现不匹配的情况,那就让子串的指针回到子串的第一个字符,主串的指针回到与子串第一个字符配对的下一个字符。当循环遍历结束时,如果
子串指针j>子串长度,那就说明主串中有与子串匹配的字符串。此时,主串指针减去子串指针的值主串与子串匹配的字符串的第一个字符的下标。BF算法最坏情况下的时间复杂度=主串的长度,最好情况下的时间复杂度=子串长度。

-
串的KMP算法:KMP算法是BF算法的改进。BF算法是一种暴力匹配方法,即出现不匹配的情况后,直接丢弃前面已匹配的信息,重新开始对子串和主串匹配,直到主串结束或出现匹配情况。这种方法极大地降低了匹配效率。而在KMP算法中,对于每一个模式串我们会事先计算出模式串的内部匹配信息,在匹配失败时最大的移动模式串,以减少匹配次数。比如,在简单的一次匹配失败后,我们会想将模式串尽量的右移和主串进行匹配。右移的距离在KMP算法中是如此计算的:在已经匹配的模式串子串中,找出最长的相同的前缀和后缀,然后移动使它们重叠。然而,如果每次都要计算最长的相同的前缀反而会浪费时间,所以对于模式串来说,我们会提前计算出每个匹配失败的位置应该移动的距离也就是
nextv数组和nextval数组,花费的时间就成了常数时间。


-
KMP算法具体代码(pta 7-2 jmu-ds-实现KMP)
-
#include<iostream>
#include<string>
#include<vector>
using namespace std;
void GetNext(string str,int next[]);
void GetNextval(string str,int next[],int nextval[]);
int KMPIndex(string Mstr, string Sstr);
int main()
{
int num,i;
string Mdata[100];
string Sdata[100];
int index;
cin >> num;
for (i = 0; i < num; i++)
{
cin >> Mdata[i];
cin >> Sdata[i];
index=KMPIndex(Mdata[i], Sdata[i]);
if (index != -1)
{
cout << index << endl;
}
else
{
cout << "not find!"<<endl;
}
}
}
void GetNext(string str,int next[])
{
int j, k;
j = 0; k = -1;
next[0] = -1;
while (j < str.length()-1)
{
if (k == -1 || str[j] == str[k])
{
j++, k++;
next[j] = k;
}
else
{
k = next[k];
}
}
}
void GetNextval(string str, int next[],int nextval[])
{
int j = 0, k = -1;
nextval[0] = -1;
while (j < str.length())
{
if (k == -1 || str[j] == str[k])
{
j++, k++;
if (str[j] != str[k])
{
nextval[j] = next[j];
}
else
{
nextval[j] = nextval[k];
}
}
else
{
k = nextval[k];
}
}
}
int KMPIndex(string Mstr, string Sstr)
{
int next[100], nextval[100];
int i = 0,j = 0;
GetNext(Sstr,next);
GetNextval(Sstr, next,nextval);
int Mlen, Slen;
Mlen = Mstr.size();
Slen = Sstr.size();
while (i < Mlen&& j < Slen)
{
if (j == -1 || Mstr[i] == Sstr[j])
{
i++;
j++;
}
else
{
j = nextval[j];
}
}
if (j >= Sstr.size())
{
return(i - Sstr.size());
}
else
{
return -1;
}
}
- 二叉树存储结构、建法、遍历及应用
-
二叉树存储结构:二叉树的存储结构分为顺序存储和链式存储。二叉树的顺序存储,就是用一组连续的存储单元存放二叉树中的结点。但使用这种存储结构之前必须先将二叉树的所有结点安排成为一个恰当的序列,使各个结点在这个序列中的相互位置能反映出结点之间的逻辑关系。但顺序存储结构在不知道结点数量的情况下,很有可能对存储空间造成极大的浪费,在最坏的情况下,一个
深度为k且只有k个结点的右单支树需要2k-1各存储空间。所以只有完全二叉树和满二叉树采用这种存储结构比较合适;二叉树的链式存储结构是只用链表来表示一棵二叉树,即用链来表示各结点之间的逻辑关系。通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。
为了方便访问某结点的双亲,还可以给链表结点增加一个双亲指针parent,用来指向其双亲结点。即每个结点由四个域组成。


-
二叉树的遍历:二叉树的遍历同样有四种方法:前序遍历、中序遍历、后续遍历、层序遍历。
- 二叉树的前序遍历:若树为空,则空操作返回。否则,先访问根节点,然后前序遍历左子树,再前序遍历右子树。
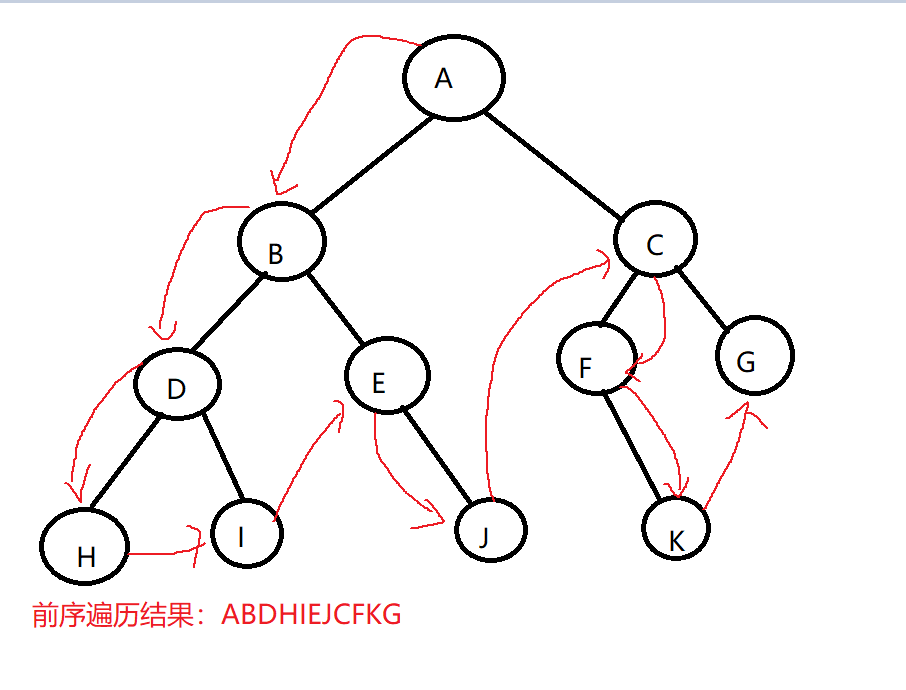
- 二叉树的中序遍历:若树为空,则空操作返回。否则,从根节点开始(注意并不是先访问根节点),中序遍历根节点的左子树,然后是访问根节点,最后中序遍历根节点的右子树。
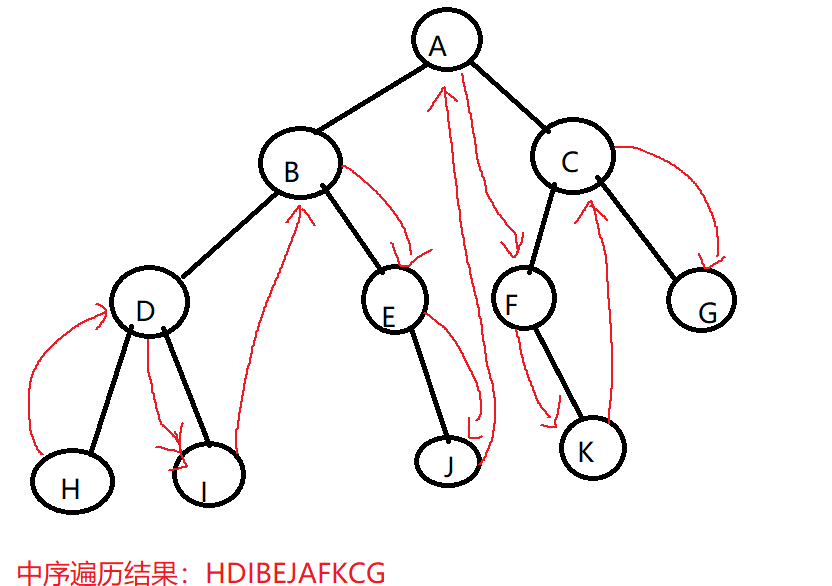
- 二叉树的后序遍历:若树为空,则空操作返回。否则,从左到右先叶子后节点的方式遍历访问左右子树,最后访问根节点。
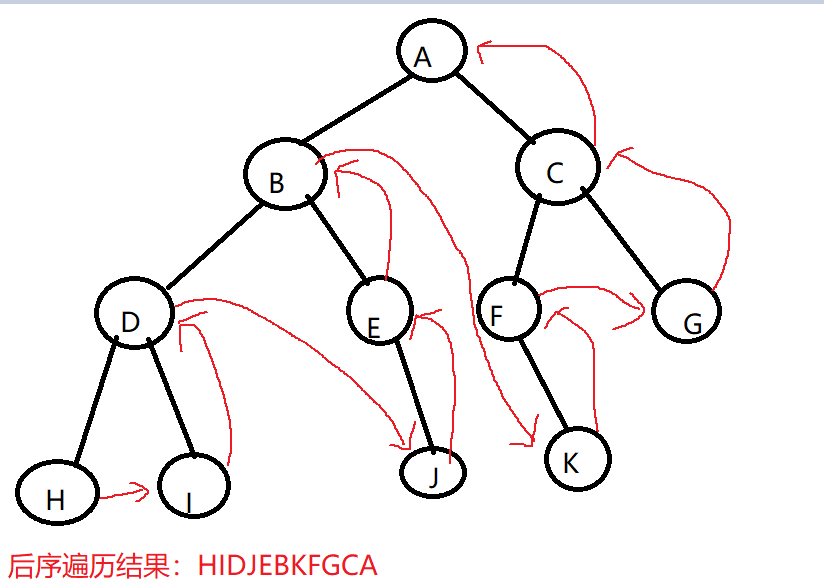
- 二叉树的层序遍历:若树为空,则空操作返回。否则,从树的第一层,也就是根节点开始访问,从上到下逐层遍历,在同一层中,按从左到右的顺序结点逐个访问。

- 二叉树的前序遍历:若树为空,则空操作返回。否则,先访问根节点,然后前序遍历左子树,再前序遍历右子树。
-
二叉树的建法:二叉树有四种建树方法:前序遍历建树、层序遍历建树、根据先序遍历和中序遍历建树、根据后续遍历和中序遍历建树。
-
TreeNode* CreateTree(char* arr, int* pi)//pta 7-1 前序序列创建二叉树
{
if (arr[*pi] == '#')
{
return NULL;
}
else
{
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
root->_val = arr[*pi];
++(*pi);
root->pleft = CreateTree(arr, pi);
++(*pi);
root->pright = CreateTree(arr, pi);
return root;
}
}
BTNode CreatBTree( string treeData,int i)//层序遍历建二叉树
{
if (!treeData[1]) return NULL;
BTNode root;
int len;
root = new BTree;
len = treeData.size();
if (i>=len||treeData[i] == '#')
{
return NULL;
}
root->data = treeData[i];
root->lchild = CreatBTree(treeData, 2 * i);
root->rchild = CreatBTree(treeData, 2 * i + 1);
return root;
}
BTNode RecoverTree(char* pre, char* in, int n)//根据先序遍历和中序遍历建二叉树
{
if (n == 0)
{
return NULL;
}
BTNode root;
root = new TNode;
int rootIndex;
root->data = *pre;
for (rootIndex = 0; rootIndex < n; rootIndex++)
{
if (in[rootIndex] == *pre)
{
break;
}
}
root->lchild = RecoverTree(pre + 1, in, rootIndex);
root->rchild = RecoverTree(pre + rootIndex + 1, in + rootIndex + 1, n - rootIndex - 1);
return root;
}
BTNode RecoverTree(int *back, int *in, int n)//根据后序和中序遍历建二叉树
{
if (n == 0)
{
return NULL;
}
BTNode root;
root = new TNode;
int rootIndex;
root->data = back[n - 1];
for (rootIndex = 0; rootIndex < n; rootIndex++)
{
if (in[rootIndex] == back[n - 1])
{
break;
}
}
root->lchild = RecoverTree(back, in, rootIndex);
root->rchild = RecoverTree(back+rootIndex, in+rootIndex+1, n -rootIndex-1);
return root;
}
-
二叉树的应用:二叉树可用于大量信息搜索的优秀数据结构。它们常用于数据库应用程序,以组织键值,建立对数据库记录的索引。而二叉树的搜索又是建立在二叉树的遍历上的,所以二叉树的应用与二叉树的遍历方式也是密不可分的。
-
树的结构、操作、遍历及应用
-
树的结构:树的每个结点有零个或多个子结点,每一个非根结点有且只有一个双亲结点,除了根节点之外,每个子结点可以分为多个不相交的子树。结点的度指结点拥有的子树的个数,树的度指数中度最大的结点的度数。二叉树其实就是一棵特殊的树,一颗树的度和所有结点的度均为2的树。
-
树的操作:结构定义、插入、查找、删除操作。
-
树的遍历:树的遍历与二叉树的遍历基本一致,这里就不作过多介绍了。
-
树的应用:由于二叉树是树的一种特殊形式,所以上述提到的二叉树的应用,树也可以。除此之外,树的应用还有字典树:用于海量文本词频统计,查询效率极高。B,B+树:广泛用于数据库的索引。哈夫曼树:下面会介绍。等等……
-
typedef struct BTree//结构定义
{
int data;
struct BTree* lchild;
struct BTree* rchild;
}TNode, * BTNode;
BTNode newnode(int v)//树的结点生成,v为结点存储的值
{
BTNode Node=new TNode;
Node->data=v;
Node->lchild=Node->rchild=NULL;//左右子树置为NULL
return Node;
}
void insert(BTNode &root,int x)//树的结点插入,x为待插入数据
{
if(root==NULL)
{
root=newnode(x);
return;
}
if(x<root->data)//待插结点值小于根节点,插入左子树
insert(root->lchild,x);
if(x>root->data)
insert(root->rchild,x);
}
int search(BTNode root,int x)//树的结点查找
{
if(root==NULL)//空树直接返回
return -1;
if(root->data==x)//找到后可以直接给出结果或者对找到的结果进行修改操作
{
printf("success\n");
return x;
}
search(root->rchild,x,newdata);//分别向左右子树递归
search(root->lchild,x,newdata);
}
void delete(BTNode &root,int x)//树的结点删除
{
BTNode node=root;
if(search(x)!=-1)
{
if(node->data==x) node=NULL; return;
delete(node->lchild,x);
delete(ndoe->rchild,x);
}
}
-
线索二叉树:
-
什么是线索二叉树:不管树的形态如何,在一棵树中,空链域的个数总是多过非空链域的个数。准确的说,一颗有n个结点的二叉树,有2n个链域,非空链域为n-1个,但却有n+1个空链域。因此,为了解决空链域造成的空间浪费,可以利用原来的空链域来存放指针,指向树中的其他结点,这种指针成为线索。
-
建立线索的规则:线索的建立与树的遍历顺序有关。这里以中序遍历为例:如果
ptr->lchild为空,则存放指向中序遍历序列中该结点的前驱结点。这个结点称为ptr的中序前驱;如果ptr->rchild为空,则存放指向中序遍历序列中该结点的后继结点。这个结点称为ptr的中序后继;为了区分左孩子和前驱、右孩子和后继,还需要两个int型的标志域ltag和rtap。ltag为0时指向该结点的左孩子,为1时指向该结点的前驱;rtag为0时指向该结点的右孩子,为1时指向该结点的后继。 -
线索二叉树的结构体定义:

-
中序线索二叉树的实现:

-
-
哈夫曼树、并查集:
-
什么是哈夫曼树:了解哈夫曼树之前先要清楚二叉树的带权路径长的概念,即一棵有n个带权的值的叶子结点的二叉树,那么从根到各个叶子结点的长度与相应结点权值乘积的和就叫做二叉树的带权路径长度,也可以用
WPL来表示。而具有最小带权路径长度的二叉树就成为哈夫曼树。 -
建立哈夫曼树的原则:权值越大的叶子结点越靠近根节点,权值越小的叶子结点越远离根节点,这样才能保证带权路径长度最小。
-
哈夫曼树的特点:由于哈夫曼树的建立过程是不断合并两个树,所以在哈夫曼树中不存在单分支结点,即不存在度为1的结点;哈夫曼树的
总结点数=2*叶子结点数-1。 -
哈夫曼树的结构体定义:
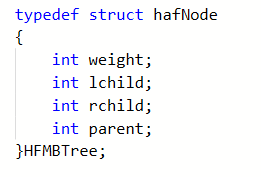
-
哈夫曼树建立代码:
-
void CreatHaf(HFMBTree haf[], int HafData[], int n)
{
int i, j;
int min1, min2;
int lnode, rnode;
for (i = 0; i < 2 * n - 1; i++)
{
haf[i].lchild = haf[i].rchild = haf[i].parent = -1;
}
for (i = 0; i < n; i++)
{
haf[i].weight = HafData[i];
}
for (i = n; i < 2 * n - 1; i++)
{
min1 = min2 = 999999;
lnode = rnode = -1;
for (j = 0; j <= i - 1; j++)
{
if (haf[j].parent == -1)
{
if (haf[j].weight < min1)
{
min2 = min1;
rnode = lnode;
min1 = haf[j].weight;
lnode = j;
}
else if (haf[j].weight < min2)
{
min2 = haf[j].weight;
rnode = j;
}
}
}
haf[lnode].parent = i;
haf[rnode].parent = i;
haf[i].weight = haf[lnode].weight + haf[rnode].weight;
haf[i].lchild = lnode;
haf[i].rchild = rnode;
}
}
-
什么是并查集:并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。简单的说就是给定一片森林中的两个结点(不一定是在同一个树中),判断这两个结点是否属于同一棵树,如果是的话就压缩其到根节点的路径,即将其直接接到根节点上,做根节点的子结点;如果两个结点不是属于同一棵树的话,就将两个元素所在的集合合并为一个集合。
-
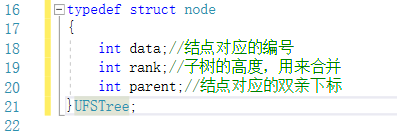
并查集的结构体定义:
-
并查集的基本操作:
void MAKE_SET(UFSTree t[], int n)//并查集的初始化
{
int i;
for (i = 1; i <= n; i++)
{
t[i].data = i;
t[i].rank = 0;
t[i].parent = i;
}
}
int FIND_SET(UFSTree t[], int x) //查找一个元素所属的集合
{
if (x != t[x].parent)
{
return (FIND_SET(t, t[x].parent));
}
else
{
return (x);//找到根节点
}
}
void UNION(UFSTree t[], int x, int y)//两个元素各自所属的集合的合并
{
x = FIND_SET(t, x);//找到x所在树的编号
y = FIND_SET(t, y);//找到y所在树的编号
//将秩小的那一棵树归并到秩大的那一棵树上
if (t[x].rank > t[y].rank)
{
t[y].parent = x;
}
else
{
t[x].parent = y;
if (t[x].rank = t[y].rank)//若秩相同则合并后的秩增1
{
t[y].rank++;
}
}
}
1.2.谈谈你对树的认识及学习体会。
- 我对树的认识:树是一种特殊的有序合集。一棵树最少有一个结点(根节点),多棵不相交的树的合集称为森林。树是一种实用性非常强大的数据结构,哈夫曼编码、海量数据并发查询、目录树、红黑树等实际运用都是通过树的结构来实现的。
c++中的STL、map和set都是通过红黑树来实现的。 - 学习体会:虽说树的泛用性很广,但是要掌握起来却没那么容易,其原因之一就是许多与树相关的操作都会用到递归,而递归最怕的就是递归出口设置错误或忘记设置递归出口,导致死循环,所以用递归来操作树时一定要注意递归出口的设置。还有就是要注意题目要求的输入和输出格式是什么顺序的,看清题目是要先序输出还是中序输出或后续、层序输出。
2.阅读代码
2.1 题目及解题代码

#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
#define MAXSIZE 100
typedef struct Node
{
char data;
struct Node* lchild, * rchild;
}BitNode, * BiTree;
void CreateBitTree(BiTree* T, char str[]);
void PrintLevel(BiTree T);
void SwapSubTree(BiTree* T);
void SwapSubTree(BiTree* T)
{
BitNode* temp;
if ((*T))
{
temp = (*T)->lchild;
(*T)->lchild = (*T)->rchild;
(*T)->rchild = temp;
SwapSubTree(&((*T)->lchild));
SwapSubTree(&((*T)->rchild));
}
}
void CreateBitTree(BiTree* T, char str[])
{
char ch;
BiTree stack[MAXSIZE];
int top = -1;
int flag, k;
BitNode* p;
*T = NULL, k = 0;
ch = str[k];
while (ch != '\0')
{
switch (ch)
{
case '(':
stack[++top] = p;
flag = 1;
break;
case ')':
top--;
break;
case ',':
flag = 2;
break;
default:
p = (BiTree)malloc(sizeof(BitNode));
p->data = ch;
p->lchild = NULL;
p->rchild = NULL;
if (*T == NULL)
{
*T = p;
}
else
{
switch (flag)
{
case 1:
stack[top]->lchild = p;
break;
case 2:
stack[top]->rchild = p;
}
}
}
ch = str[++k];
}
}
void TreePrint(BiTree T, int level)
{
int i;
if (T == NULL)
{
return;
}
TreePrint(T->rchild, level + 1);
for (i = 0; i < level; i++)
{
printf(" ");
}
printf("%c\n", T->data);
TreePrint(T->lchild, level + 1);
}
void main()
{
BiTree T;
char str[MAXSIZE];
cout << "请输入二叉树的广义表形式:" << endl;//A(B(D,E),C(F))
cin >> str;
cout << "由广义表形式的字符串构造二叉树:" << endl;
CreateBitTree(&T, str);
cout << endl << "左右子树交互前的二叉树:" << endl;
TreePrint(T, 1);
SwapSubTree(&T);
cout << endl << "左右子树交互后的二叉树:" << endl;
TreePrint(T, 1);
system("pause");
}
2.1.1 该题的设计思路
- 设计思路:利用递归。从根节点开始,交换左右两个树的指针,然后递归调用左右两棵子树,对子树的各个结点的左右两个指针进行交换。
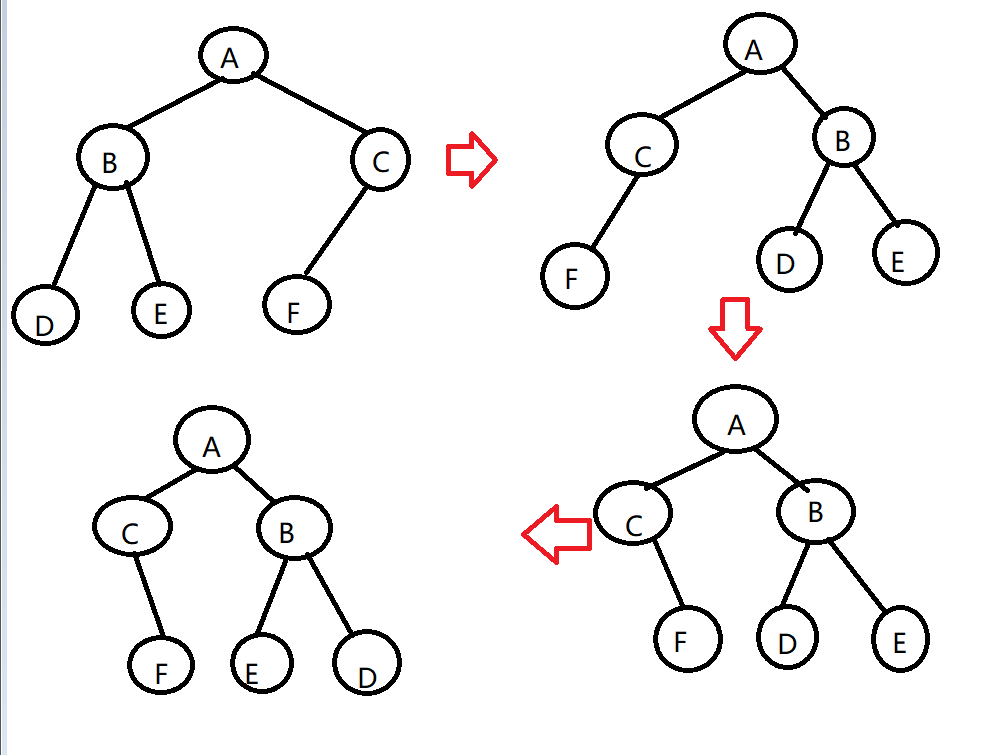
- 时间复杂度:T(n)=O(n)
- 空间复杂度:S(n)=O(n)
2.1.2 该题的伪代码
输入括号形式的二叉树;
调用CreateBitTree(&T, str)函数层序建树;
调用TreePrint(T, 1)函数输出未交换左右子树之前的二叉树;
调用SwapSubTree(&T)函数递归交换二叉树左右子树;
void SwapSubTree(BiTree *T)
{
定义二叉树结构体指针temp;
if(当前结点不为空)
temp=当前结点的左子树;
当前结点->左子树=当前结点->右子树;
SwapSubTree(&((*T)->lchild));
SwapSubTree(&((*T)->rchild));
end if
}
调用TreePrint(T, 1)输出交换左右子树后的二叉树;
2.1.3 运行结果
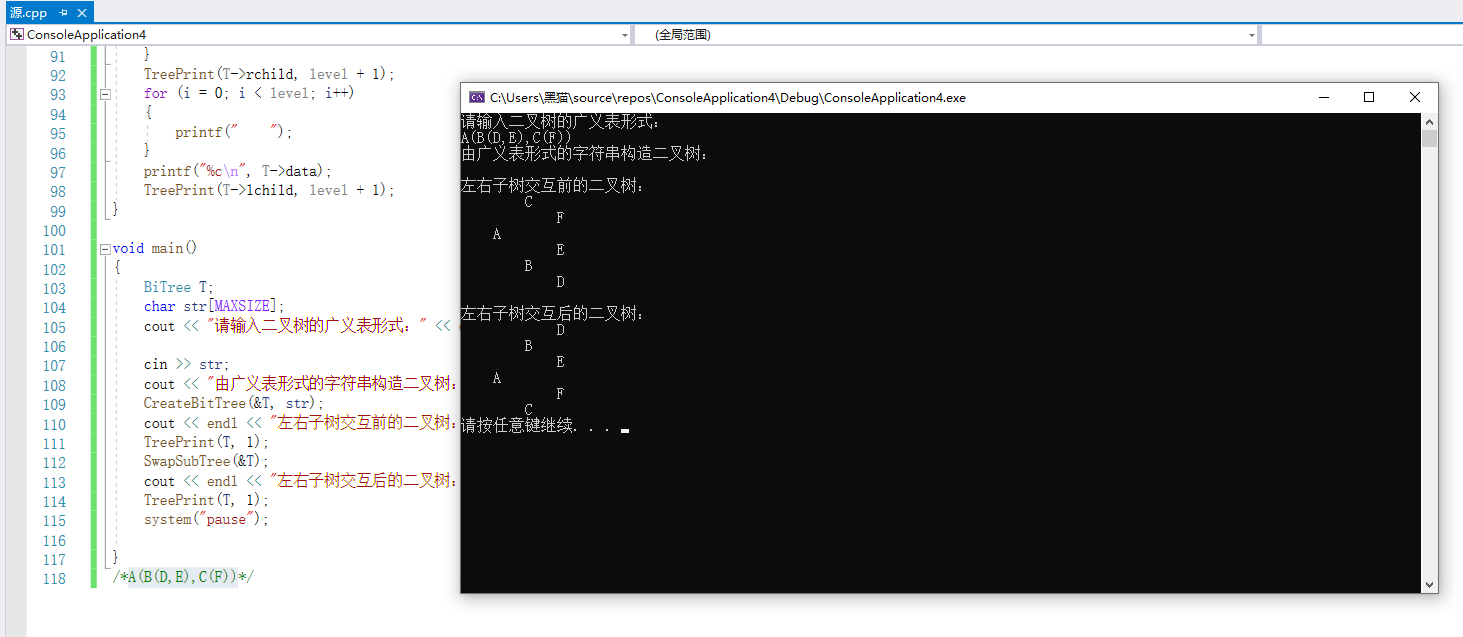
2.1.4分析该题目解题优势及难点。
- 解的题优势:二叉树的建立可以用刚学过的层序遍历法来建,对左右子树的交换也可以在前序遍历算法的基础上稍微改进一下来达到交换左右子树的效果,而且使用递归算法也大大降低了算法的时间复杂度。
- 难点:通过括号表达式来建树时要注意左右括号的配对,遇到右括号时要及时出队左括号;递归交换左右子树时要注意递归出口,否则容易造成死循环或程序崩溃;输出二叉树时还要注意当前结点的层次需要先输出几个空格。
2.2 题目及解题代码
#include <stdio.h>
#include <stdlib.h>
#include <string>
#include <iostream>
using namespace std;
#define MAXSIZE 100
typedef struct Node
{
char data;
struct Node* lchild, * rchild;
}BitNode, * BiTree;
void CreateBitTree(BiTree* T, char str[]);
void PrintLevel(BiTree T);
void CreateBitTree(BiTree* T, char str[])
{
char ch;
BiTree stack[MAXSIZE];
int top = -1;
int flag, k;
BitNode* p;
*T = NULL, k = 0;
ch = str[k];
while (ch != '\0')
{
switch (ch)
{
case '(':
stack[++top] = p;
flag = 1;
break;
case ')':
top--;
break;
case ',':
flag = 2;
break;
default:
p = (BiTree)malloc(sizeof(BitNode));
p->data = ch;
p->lchild = NULL;
p->rchild = NULL;
if (*T == NULL)
{
*T = p;
}
else
{
switch (flag)
{
case 1:
stack[top]->lchild = p;
break;
case 2:
stack[top]->rchild = p;
break;
}
}
}
ch = str[++k];
}
}
void TreePrint(BiTree T, int level)
{
int i;
if (T == NULL)
{
return;
}
TreePrint(T->rchild, level + 1);
for (i = 0; i < level; i++)
{
printf(" ");
}
printf("%c\n", T->data);
TreePrint(T->lchild, level + 1);
}
int BiTreeDepth(BiTree T)
{
if (T == NULL)
{
return 0;
}
return BiTreeDepth(T->lchild) > BiTreeDepth(T->rchild) ? 1 + BiTreeDepth(T->lchild) : 1 + BiTreeDepth(T->rchild);
}
int BiTreeWidth(BiTree T)
{
int front, rear, last, maxw, temp;
BiTree Q[MAXSIZE];
BitNode* p;
if (T == NULL)
{
return 0;
}
else
{
front = 1, rear = 1, last = 1;
temp = 0;
maxw = 0;
Q[rear] = T;
while (front <= last)
{
p = Q[front++];
temp++;
if (p->lchild != NULL)
{
Q[++rear] = p->lchild;
}
if (p->rchild != NULL)
{
Q[++rear] = p->rchild;
}
if (front > last)
{
last = rear;
if (temp > maxw)
{
maxw = temp;
}
temp = 0;
}
}
return maxw;
}
}
void main()
{
BiTree T;
char str[MAXSIZE];
cout << "请输入二叉树的广义表形式:" << endl;
cin >> str;
cout << "由广义表形式的字符串构造二叉树:" << endl;
CreateBitTree(&T, str);
cout << endl;
TreePrint(T, 1);
cout << endl;
cout << "这棵树的高度为:" << BiTreeDepth(T) << endl;
cout << "这棵树的最大宽度为:" << BiTreeWidth(T) << endl;
system("pause");
//A(B(D(H,I),E),C(F,G))
}
2.2.1 该题的设计思路
- 设计思路:用层序遍历求二叉树的最大宽度:依次将每一层中结点指针入队列,然后再分别将当前的指针出队,统计其结点个数,并将下一层结点指针入队,记录每一层结点个数,可得出结点个数最大值。遍历完毕后,结点个数最大值就是二叉树的最大宽度;分别遍历二叉树左右子树求高度,左右子树高度的最大值再加1就是二叉树的高度。
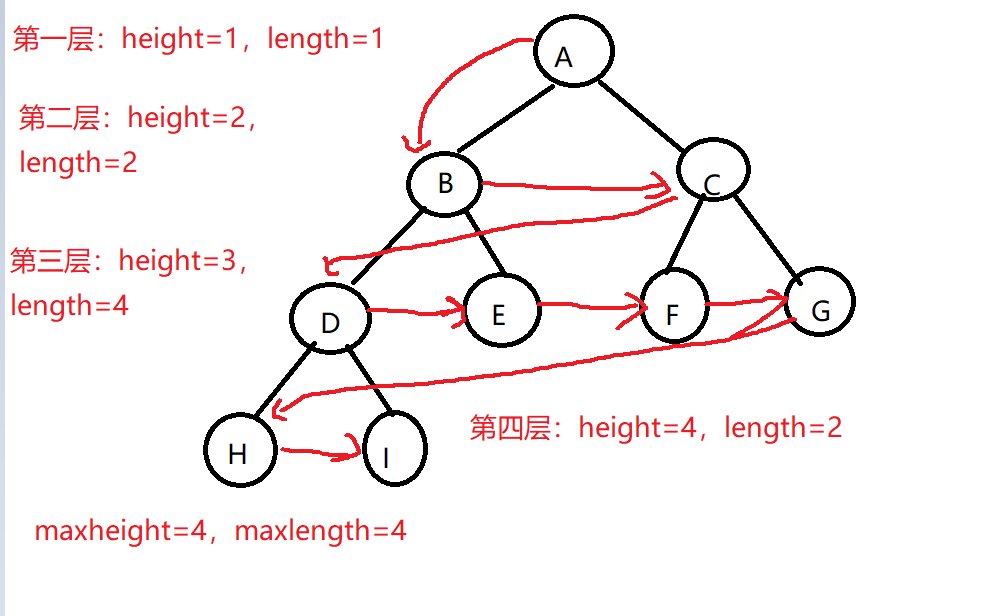
- 时间复杂度:T(n)=O(n)
- 空间复杂度:S(n)=O(n)
2.2.2 该题的伪代码
输入二叉树括号表达式字符串;
调用CreateBitTree(&T, str)函数层序建立二叉树;
调用TreePrint(T, 1)函数输出二叉树的结构图;
调用BiTreeDepth(T)函数求二叉树的最大高度;
int BiTreeDepth(BiTree T)
{
if(当前结点为空)
return 0;
end if
if(BiTreeDepth(T->lchild) > BiTreeDepth(T->rchild))
return BiTreeDepth(T->lchild)+1;
else
return BiTreeDepth(T->rchild)+1;
}
调用BiTreeWidth(T)函数求二叉树的最大宽度;
int BiTreeWidth(BiTree T)
{
if(当前结点为空) return 0;
else
根节点入队,int temp=maxw=0;
while(队不为空)
取队头结点p后出队队头结点,temp++;
if(p的左孩子不空) 入队;
if(p的右孩子不空) 入队;
if(temp>maxw) maxw=temp;
temp=0;
end while
return maxw;
}
2.2.3 运行结果
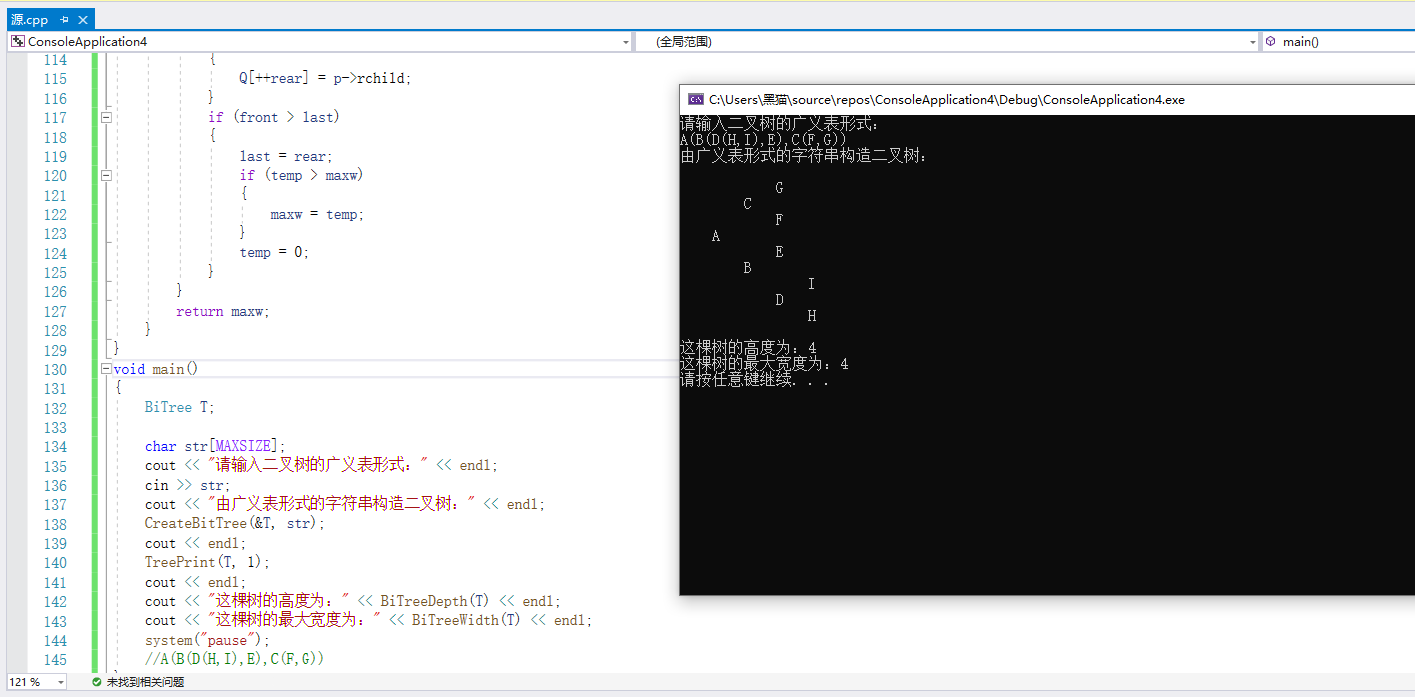
2.2.4 分析该题目解题优势及难点。
- 解题优势:可以用
c++的STL容器queue来层序建二叉树和层序遍历二叉树;用递归算法来求二叉树的高度,时间效率高。 - 难点:同上,括号表达式建二叉树要注意左右括号的匹配;求二叉树深度时,返回左右子树中最大高度还要加上1(根节点);用队列层序遍历二叉树时要注意判断队空,否则会引发编译器报错。
2.3 题目及解题代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
using namespace std;
#include <iomanip>
typedef char DataType;
#define MAXSIZE 100
typedef struct Node
{
DataType data;
struct Node* lchild, * rchild;
}BitNode, * BiTree;
void CreateBitTree(BiTree* T, char str[]);
void PrintLevel(BiTree T);
void CreateBitTree(BiTree* T, char str[])
{
char ch;
BiTree stack[MAXSIZE];
int top = -1;
int flag, k;
BitNode* p=NULL;
*T = NULL, k = 0;
ch = str[k];
while (ch != '\0')
{
switch (ch)
{
case '(':
stack[++top] = p;
flag = 1;
break;
case ')':
top--;
break;
case ',':
flag = 2;
break;
default:
p = (BiTree)malloc(sizeof(BitNode));
p->data = ch;
p->lchild = NULL;
p->rchild = NULL;
if (*T == NULL)
{
*T = p;
}
else
{
switch (flag)
{
case 1:
stack[top]->lchild = p;
break;
case 2:
stack[top]->rchild = p;
break;
}
}
}
ch = str[++k];
}
}
void TreePrint(BiTree T, int level)
{
int i;
if (T == NULL)
{
return;
}
TreePrint(T->rchild, level + 1);
for (i = 0; i < level; i++)
{
printf(" ");
}
printf("%c\n", T->data);
TreePrint(T->lchild, level + 1);
}
void Path(BiTree root, BitNode* r)
{
BitNode* p, * q;
int i, top = 0;
BitNode* s[MAXSIZE];
q = NULL;
p = root;
while (p != NULL || top != 0)
{
while (p != NULL)
{
top++;
if (top >= MAXSIZE)
{
exit(-1);
}
s[top] = p;
p = p->lchild;
}
if (top > 0)
{
p = s[top];
if (p->lchild == NULL || p->rchild == q)
{
if (p == r)
{
for (i = 1; i <= top; i++)
{
cout << setw(4) << s[i]->data;
}
top = 0; p = NULL;
}
else
{
q = p;
top--;
p = NULL;
}
}
else
{
p = p->rchild;
}
}
}
}
BiTree FindPointer(BiTree T, DataType e)
{
BiTree Q[MAXSIZE];
int front = 0, rear = 0;
BitNode* p;
if (T)
{
Q[rear] = T;
rear++;
while (front != rear)
{
p = Q[front];
front++;
if (p->data == e)
{
return p;
}
if (p->lchild)
{
Q[rear] = p->lchild;
rear++;
}
if (p->rchild)
{
Q[rear] = p->rchild;
rear++;
}
}
}
return NULL;
}
void main()
{
BiTree T;
BitNode* s;
DataType e;
char str[MAXSIZE];
cout << "请输入二叉树的广义表形式:" << endl;
cin >> str;
cout << "由广义表形式的字符串构造二叉树:" << endl;
CreateBitTree(&T, str);
TreePrint(T, 1);
cout << "请输入一个结点:" << endl;
cin >> e;
s = FindPointer(T, e);
cout << "从根结点到结点元素" << e << "之间路径上的结点为:" << endl;
Path(T, s);
cout << endl;
system("pause");
//(A(B(D(H,I),E),C(F(J),G)))
}
2.3.1 该题的设计思路
-
设计思路:采用后续遍历,遍历二叉树。当访问到目标结点时,此时栈中所有结点均为目标结点的祖先,由这些祖先便可构成一条从根节点到目标结点之间的路径。

- 时间复杂度:T(n)=O(n²)
- 空间复杂度:S(n)=O(n)
2.3.2 该题的伪代码
输入二叉树的括号表达式;
调用CreateBitTree(&T,str)层序遍历建二叉树;
调用TreePrint(T, 1)函数输出二叉树结构图;
输入目标结点;
调用s = FindPointer(T, e)函数查找目标节点在二叉树中位置;
调用Path(T, s)输出根结点到目标结点之间的路径;
void Path(BiTree root, BitNode *r)
{
q=NULL;
while(当前结点不为空||栈不空)
while(遍历左子树)
将左子树全部入栈
end while
if(栈不空)
取栈顶结点p;
if(p的左孩子为空||p的右孩子==q)
if(p为目标结点) 顺序输出当前栈中所有结点,结束循环;
else q=p,出栈栈顶元素,p=NULL;
else 查找右子树p->rchild;
end while
}
2.3.3 运行结果
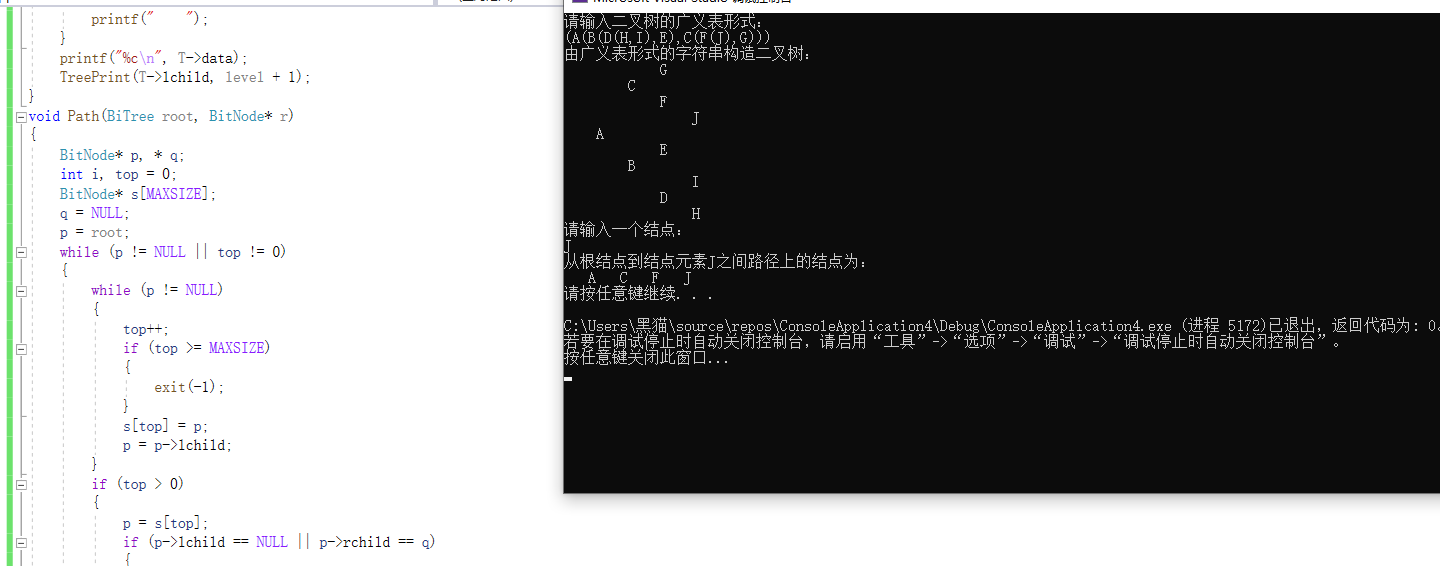
2.3.4分析该题目解题优势及难点。
- 解题优势:可以利用
c++中的STL容器stack来进行遍历和查找结点操作。可以利用c++中的STL容器queue来建二叉树。在输出路径时也可以利用栈转换成队列来输出路径。 - 难点:建二叉树时要注意左右括号的匹配;建树过程中要注意判断队列是否为空,否则容易引起编译器报错;在利用栈进行遍历时要注意判断栈是否为空,否则也很容易引起编译器报错;在查找结点时要注意在访问完一个结点后就要出栈该结点。
2.4 题目及解题代码
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == p || root == q || root == NULL) return root;
TreeNode* left = lowestCommonAncestor(root -> left, p, q);
TreeNode* right = lowestCommonAncestor(root -> right, p, q);
if (left && right) return root;
return left ? left : right;
}
};
作者:z1m
链接:https://leetcode-cn.com/problems/first-common-ancestor-lcci/solution/di-gui-jie-fa-python-3-c-by-z1m/
来源:力扣(LeetCode)
2.4.1 该题的设计思路
-
设计思路:用先序遍历创建二叉树,找到两个目标结点在二叉树中的位置,如果两个结点分别在二叉树的左右子树,则结点就是根结点;否则就将根结点看作两个结点所在的子树的根节点,然后重复以上步骤,直至两个结点在同一棵子树或新的子树的度为2,则该新的根节点即为最近两个结点的首个公共祖先。

- 时间复杂度:T(n)=O(n)
- 空间复杂度:S(n)=O(n)
2.4.2 该题的伪代码
输入先序遍历字符串;
通过先序遍历字符串建二叉树;
输入两个目标结点数据e1,e2;
调用FindPointer函数查找并返回目标结点在二叉树中的位置targ1,targ2;
调用LowestAnc函数查找并返回两个目标结点的首个公共祖先anc;
TreeNode* LowestAnc(TreeNode* pRoot, TreeNode* target1, TreeNode* target2)
{
if(树空) return NULL;
if(找到目标结点1或2) return 目标结点1或2;
else 在左子树和右子树中继续递归查找目标结点;
if(两个目标结点分别在左右子树) return 根节点;
if(只在左子树或右子树中找到目标结点) return 目标结点;
}
输出首个公共祖先anc的数据;
2.4.3 运行结果

2.4.4 分析该题目解题优势及难点。
- 解题优势:题目要求是二叉树,所以只需要考虑左右子树,判断目标结点在二叉树中的位置即可确定首个公共祖先;可以用递归算法一边遍历二叉树一边查找和判断目标结点的位置,时间效率高。
- 难点:如果两棵个目标结点在同一子树上的话,在调用递归时要注意更新根节点,即该子树的根节点即为新的根节点,如果没有更新根节点的话程序会陷入死循环;前序遍历法建二叉树,如果用递归法建二叉树的话要注意递归出口的设置,否则可能会引发系统报错。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号