「闲话随笔」势能分析法
「闲话随笔」势能分析法
这闲话已经被催了两天了,累死我了。
感谢 joke3579 帮我找到了 Tarjan 的论文。虽然没看懂只截了一下里面的图。
语文考了 82,需要单独给语文老师发作业,很闹心。
今日推歌:盲龙默虎 feat.洛天依 vs 言和。
iKz 老师的《一年一度武斗大赛》系列是不是快要更了?
简介
一种挺神奇的分析时间复杂度的方法。
一个算法/数据结构单次操作的复杂度难以计算时可以用势能分析法。
分析
设第 \(i\) 次操作的时间复杂度为 \(a_i\),显然总复杂度为 \(\sum_{i=1}^{n}a_i\)。
构造一个势能函数 \(\phi(i)\) 表示第 \(i\) 次操作后的势能,设 \(\Delta_{\phi(i)}\) 表示单次的势能变化,即 \(\Delta_{\phi(i)}=\phi(i)-\phi(i-1)\)。
设摊还代价 \(b_i=a_i+\Delta_{\phi(i)}\),则:
不知道我在说什么,对不对?看起来啥用没有,对不对?
不对就怪了
实际上我们虽然无法算出具体的 \(a_i\),但是可以用未知数表示出来,这个时候构造一个优秀的势能函数,就可以巧妙地将 \(b_i\) 化为一个数或是求出其上限。
看看例题就都明白了。
例题
二进制计数器
题意:
一个二进制下的计数器,每次累加 \(1\),做 \(n\) 次累加,求操作的次数。
定义一次操作为一位上发生变化,因此每次累加 \(1\) 可能会带有多次操作。
设每次累加会有 \(x\) 位 \(1\) 变为 \(0\),那么 \(a_i=x+1\)(还会有一个 \(0\) 变为 \(1\))。
那么构造势能函数 \(\phi(i)\) 表示累加 \(i\) 次后数字里有多少个一。
显然 \(\Delta_{\phi(i)}=1-x\)。
然后就发生了一件神奇的事:\(b_i=(x+1)+(1-x)=2\)!
然后化简原式得到复杂度 \(2n-\phi(n)\le 2n\)。
单调栈
不会单调栈就来学这个是不是有点过猛了。
显然单调栈不用这么麻烦地分析,但确实可以这么用。
设每次操作会有 \(x\) 个元素弹出,\(1\) 个元素加入,那么 \(a_i=x+1\)。
那么构造势能函数 \(\phi(i)\) 表示当前栈内元素个数。
显然 \(\Delta_{\phi(i)}=1-x\)。
然后就发生了一件神奇的事:\(b_i=(x+1)+(1-x)=2\)!
然后化简原式得到复杂度 \(2n-\phi(n)\le 2n\)。
然后还发生了一件神奇的事:这个过程和上个过程居然没啥区别。
Splay
默认读者已经会 splay 了,不会的话去网上搜 或者等我平衡树学习笔记写完了再看
定义 \(x\) 为一棵 splay 上的一个节点,\(x'\) 为 \(x\) 旋一次后的位置,\(\left|x\right|\) 为以 \(x\) 为根的子树的大小,\(\phi_{j}(x)=\log_{2}\left|x\right|\) 为一次 splay 操作中第 \(j\) 次操作后节点 \(x\) 的势能,\(\Phi_j\) 为一次 splay 操作中第 \(j\) 次操作后整棵树的势能。
然后我们开始分析三种旋转情况的 \(a_i\):
-
旋上根(\(\text{zig}\)):
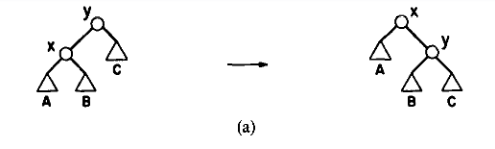
可以发现转一次只会有 \(x\) 和 \(y\) 的势能发生变化。
显然 \(\phi_{j}(x)=\phi_{j-1}(y)\)。
\[\begin{aligned} b_{\text{zig}}&=a_j+\Delta_{\Phi_j}\\ &=1+\phi_{j}(x)+\phi_{j}(y)-\phi_{j-1}(x)-\phi_{j-1}(y)\\ &=1+\phi_{j}(y)-\phi_{j-1}(x)\\ &\le\phi_{j}(x)-\phi_{j-1}(x)\\ \end{aligned} \] -
三点共线(\(\text{zig-zig}\)):
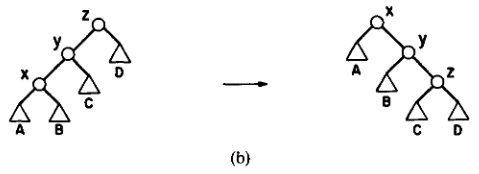
可以发现转一次只会有 \(x,y\) 和 \(z\) 的势能发生变化。
显然 \(\phi_{j}(x)=\phi_{j-1}(z)\)。
\[\begin{aligned} b_{\text{zig-zig}}&=a_j+\Delta_{\Phi_j}\\ &=2+\phi_{j}(x)+\phi_{j}(y)+\phi_{j}(z)-\phi_{j-1}(x)-\phi_{j-1}(y)-\phi_{j-1}(z)\\ &=2+\phi_{j}(y)+\phi_{j}(z)-\phi_{j-1}(x)-\phi_{j-1}(y)\\ \end{aligned} \]注意到这个 \(2\) 长得很难看,尝试把它去掉。
不难发现 \(\left|x\right|+\left|z'\right|+1=\left|x'\right|\),因此 \(\left|x'\right|^2>4\cdot\left|x\right|\cdot\left|z'\right|\),那么:
\[\phi_{j-1}(x)+\phi_{j}(z)-2\phi_{j}(x)=\log_2\frac{\left|x\right|\cdot\left|z'\right|}{\left|x'\right|^2}\le\log_2\frac{1}{4}=-2 \]然后代入一下原式:
\[\begin{aligned} b_{\text{zig-zig}}&=2+\phi_{j}(y)+\phi_{j}(z)-\phi_{j-1}(x)-\phi_{j-1}(y)\\ &=2\phi_{j}(x)-\phi_{j-1}(x)-\phi_{j}(z)+\phi_{j}(y)+\phi_{j}(z)-\phi_{j-1}(x)-\phi_{j-1}(y)\\ &=2\phi_{j}(x)-2\phi_{j-1}(x)+\phi_{j}(y)-\phi_{j-1}(y)\\ &\le3(\phi_{j}(x)-\phi_{j-1}(x)) \end{aligned} \]这样就求出了它的上限。
-
三点不共线(\(\text{zig-zag}\)):
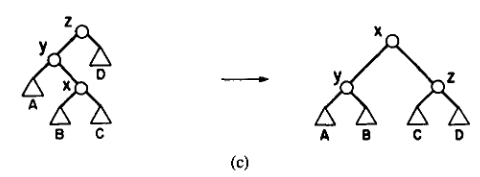
比较像上面的式子。
\[\begin{aligned} b_{\text{zig-zag}}&=a_j+\Delta_{\Phi_j}\\ &=2+\phi_{j}(x)+\phi_{j}(y)+\phi_{j}(z)-\phi_{j-1}(x)-\phi_{j-1}(y)-\phi_{j-1}(z)\\ &=2+\phi_{j}(y)+\phi_{j}(z)-\phi_{j-1}(x)-\phi_{j-1}(y)\\ \end{aligned} \]然后由于 \(\left|y'\right|+\left|z'\right|+1=\left|x'\right|\):
\[\phi_{j}(y)+\phi_{j}(z)-2\phi_{j}(x)=\log_2\frac{\left|y'\right|\cdot\left|z'\right|}{\left|x'\right|^2}\le\log_2\frac{1}{4}=-2 \]然后代入原式:
\[\begin{aligned} b_{\text{zig-zag}}&=2+\phi_{j}(y)+\phi_{j}(z)-\phi_{j-1}(x)-\phi_{j-1}(y)\\ &=2\phi_{j}(x)-\phi_{j}(y)-\phi_{j}(z)+\phi_{j}(y)+\phi_{j}(z)-\phi_{j-1}(x)-\phi_{j-1}(y)\\ &=2\phi_{j}(x)-\phi_{j-1}(x)-\phi_{j-1}(y)\\ &\le2(\phi_{j}(x)-\phi_{j-1}(x)) \end{aligned} \]
现在我们把三种旋转的摊还代价算出来了,问题变成了如何算出一次 splay 操作的摊还代价。
显然一次 splay 操作会进行若干次 \(\text{zig-zig}\), \(\text{zig-zag}\) 和至多一次 \(\text{zig}\),且三者上限都不超过 \(3(\phi_{j}(x)-\phi_{j-1}(x))\),那么:
然后由于 \(0\le\Phi_i\le n\log_2n\),\(-n\log_2n\le\Phi_0-\Phi_n\le n\log_2n\)。
所以总复杂度为:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号