「学习笔记」矩阵乘法与矩阵快速幂
「学习笔记」矩阵乘法与矩阵快速幂
点击查看目录
矩阵乘
算法
矩阵 \(A\) 规模为 \(n\times m\),矩阵 \(B\) 规模为 \(m\times q\),设 \(C=A\times B\),则:
代码
点击查看代码
const ll N=110,inf=1ll<<40;
ll n,m,p;
class Matrix{
public:
ll mat[N][N];
inline ll* operator[](ll x){return mat[x];}
inline Matrix operator*(Matrix ma)const{
Matrix mt;
_for(i,1,n){
_for(j,1,p){
mt[i][j]=0;
_for(k,1,m)mt[i][j]+=mat[i][k]*ma[k][j];
}
}
return mt;
}
}a,b;
inline void print(Matrix ma){
_for(i,1,n){
_for(j,1,p)printf("%lld ",ma[i][j]);
puts("");
}
return;
}
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline void In(){
n=rnt(),m=rnt();
_for(i,1,n)_for(j,1,m)a[i][j]=rnt();
p=rnt();
_for(i,1,m)_for(j,1,p)b[i][j]=rnt();
print(a*b);
return;
}
}
矩阵快速幂
算法
没啥好说的吧(
重载一下运算符然后冲一个矩阵快速幂就行了。
用处
- 优化递推式,例:斐波那契数列
代码(模板题)
点击查看代码
const ll N=110,P=1e9+7,inf=1ll<<40;
ll n,k;
class Mat{
public:
ll a[N][N];
inline ll* operator[](ll x){return a[x];}
inline void one(){_for(i,1,n)a[i][i]=1;}
inline Mat operator*(Mat ma){
Mat mt;
_for(i,1,n){
_for(j,1,n){
mt[i][j]=0;
_for(k,1,n)mt[i][j]=(mt[i][j]+a[i][k]*ma[k][j]%P)%P;
}
}
return mt;
}
}a;
inline void printf(Mat ma){
_for(i,1,n){
_for(j,1,n)printf("%lld ",ma[i][j]);
puts("");
}
return;
}
inline Mat fpow(Mat ma,ll b){
Mat ans;ans.one();
while(b){
if(b&1)ans=ans*ma;
ma=ma*ma,b>>=1;
}
return ans;
}
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline void In(){
n=rnt(),k=rnt();
_for(i,1,n)_for(j,1,n)a[i][j]=rnt();
printf(fpow(a,k));
return;
}
}
练习题
斐波那契数列
思路
众所周知斐波那契数列的递推式是 \(Fib_n=Fib_{n-1}+Fib_{n-2}\),\(\Theta(n)\) 本可以解决,但本题 \(n<2^{63}\),显然需要 \(\log_2n\) 算法,考虑优化。
我们设 \(F(n)\) 表示矩阵 \(\left[Fib_n,Fib_{n-1}\right]\),如果我们要把它变成 \(F(n+1)=\left[Fib_{n+1},Fib_n\right]\),则需要把 \(F(n)_{1,1}\) 挪到 \(F(n+1)_{1,2}\) ,把 \(F(n)_{1,1}+F(n)_{1,2}\) 挪到 \(F(n+1)_{1,1}\)。
尝试用矩阵优化这个东西。
我们可以发现:
那么设 \(M=\left[\begin{matrix}1&1\\1&0\end{matrix}\right]\),则:
然后冲一个矩阵快速幂就行了。
代码
点击查看代码
const ll N=5,inf=1ll<<40;
ll n,m;
class Mat{
public:
ll a[N][N];
inline ll* operator[](ll x){return a[x];}
friend Mat Mul(Mat m1,Mat m2){
Mat an;
_for(i,1,2){
_for(j,1,2){
an[i][j]=0;
_for(k,1,2)an[i][j]=(an[i][j]+m1[i][k]*m2[k][j]%m)%m;
}
}
return an;
}
};
inline Mat fpow(ll b){
Mat ans;ans[1][1]=ans[1][2]=1,ans[2][1]=ans[2][2]=0;
Mat ma;ma[1][1]=ma[1][2]=ma[2][1]=1,ma[2][2]=0;
while(b>0){
if(b&1)ans=Mul(ans,ma);
ma=Mul(ma,ma),b>>=1;
}
return ans;
}
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline void In(){
n=rnt(),m=rnt();
Mat ans=fpow(n-2);
printf("%lld\n",ans[1][1]);
return;
}
}
[SCOI2009] 迷路
思路
设 \(f_{i,j}\) 表示 \(j\) 时刻到点 \(i\) 的方案数,转移方程:
不是很可做,那我们先考虑边权只有 \(0\) 和 \(1\)的情况,可以发现转移方程能直接这样写:
发现又是个矩阵乘法,直接冲一个矩阵快速幂就行了。
但是本题边权不只有 \(0\) 和 \(1\),不能直接冲。
那么我们对一个点进行拆点,如下图:
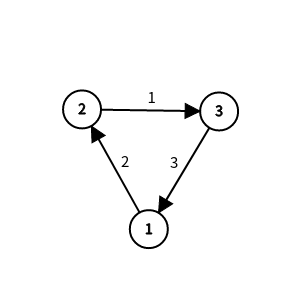
拆成
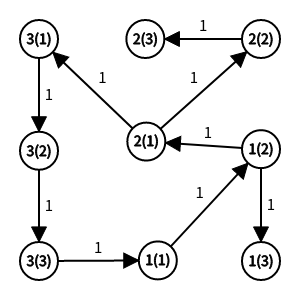
看起来有点复杂,但懂了之后好理解的。
拆完之后直接冲一个矩阵快速幂就行了。
开做发现冲一个矩阵快速幂就行了。
然而有一个边权不一定为一的限制,所以暴力把点拆进一个矩阵,就可以只用矩阵快速幂来做这道题了。
代码
点击查看代码
const ll N=110,P=2009,inf=1ll<<40;
ll n,m,t,g[N][N];
class Mat{
public:
ll a[N][N];
inline ll* operator[](ll x){return a[x];}
inline void one(){_for(i,1,m)a[i][i]=1;return;}
inline Mat operator*(Mat ma){
Mat ans;
_for(i,1,m){
_for(j,1,m){
ans[i][j]=0;
_for(k,1,m)ans[i][j]=(ans[i][j]+a[i][k]*ma[k][j]%P)%P;
}
}
return ans;
}
}tu;
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline ll rsnt(){
char c=getchar();
while(!isdigit(c))c=getchar();
return (c^48);
}
inline Mat fpow(Mat ma,ll b){
Mat ans;ans.one();
while(b){
if(b&1)ans=ans*ma;
ma=ma*ma,b>>=1;
}
return ans;
}
inline void Zhuan(){
_for(i,1,n){
_for(j,1,9){
ll k=10*(i-1)+j;
tu[k][k+1]=1;
}
_for(j,1,n){
ll k1=10*(i-1);
ll k2=10*(j-1);
if(g[i][j])tu[k1+g[i][j]][k2+1]=1;
}
}
return;
}
inline void In(){
n=rnt(),t=rnt();
_for(i,1,n)_for(j,1,n)g[i][j]=rsnt();
m=10*n,Zhuan();
Mat ans=fpow(tu,t);
printf("%lld\n",ans[1][m-9]);
return;
}
}
佳佳的 Fibonacci
思路
题目背景有时候不是白给的。
这道题中,联系题目背景可以发现原式可以化简为:
通过题目背景可知:
可这(指 \(S(n)\))对佳佳来说还是小菜一碟。
那么我们就去算 \(S(n)\)。好像有点断章取义。
同时,\(S(n)=S(n-1)+F_n\),所以 \(S(n)=F_{n+2}-1\)。
为啥 $F_{-1}=1$ 啊?
然后往原式子里带:
然后冲一个矩阵快速幂就行了。
代码
点击查看代码
const ll N=110,inf=1ll<<40;
ll n,m;
class Mat{
public:
ll a[N][N];
inline ll* operator[](ll x){return a[x];}
inline void one(){a[1][1]=a[1][2]=1;}
inline Mat operator*(Mat ma){
Mat ans;
_for(i,1,2){
_for(j,1,2){
ans[i][j]=0;
_for(k,1,2)ans[i][j]=(ans[i][j]+a[i][k]*ma[k][j]%m)%m;
}
}
return ans;
}
};
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline Mat fpow(Mat ma,ll b){
Mat ans;ans.one();
while(b){
if(b&1)ans=ans*ma;
ma=ma*ma,b>>=1;
}
return ans;
}
inline void In(){
n=rnt(),m=rnt();
Mat mat;mat[1][1]=mat[1][2]=mat[2][1]=1;
Mat ans=fpow(mat,n+1);
printf("%lld\n",(n*ans[1][2]%m-ans[1][1]+m+2)%m);
return;
}
}
选拔队员(不知道教练从哪里找的)
题意
选出若干个男生和若干多个女生(即男女生的数目随便定)安排到机房内的 \(N\) 个位置上去,要求任意两位女生不能相邻(即任意两个女生之间必须有至少一个男生),求方案数 \(\bmod{M}\)。
思路
直接用排列推是不行的,尝试写个 \(\text{dp}\)。
设 \(f_{i,0}\) 表示有 \(n\) 个人坐了上去,最后一个人是男; \(f_{i,1}\) 表示有 \(n\) 个人坐了上去,最后一个人是女。
初始状态为 \(f_{i,0}=f_{i,1}=1\),显然有递推式:
用矩阵优化:
诶这玩意儿不就是斐波那契数列吗?!
然后冲一个矩阵快速幂就行了。
代码
点击查看代码
const ll N=110,inf=1ll<<40;
ll T,m,n;
class Mat{
public:
ll a[5][5];
inline ll* operator[](ll x){return a[x];}
inline Mat operator*(Mat ma){
Mat ans;
_for(i,1,2){
_for(j,1,2){
ans[i][j]=0;
_for(k,1,2)ans[i][j]=(ans[i][j]+a[i][k]*ma[k][j]%m)%m;
}
}
return ans;
}
};
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline Mat fpow(ll b){
Mat ans;ans[1][1]=ans[1][2]=1,ans[2][1]=ans[2][2]=0;
Mat ma;ma[1][1]=ma[1][2]=ma[2][1]=1,ma[2][2]=0;
while(b){
if(b&1)ans=ans*ma;
ma=ma*ma,b>>=1;
}
return ans;
}
inline void In(){
n=rnt();
printf("%lld\n",fpow(n)[1][1]%m);
return;
}
}
Tr A
思路
不能理解这道题出的为什么这么靠后。
冲一个矩阵快速幂就行了。
代码
点击查看代码
const ll N=20,P=9973,inf=1ll<<40;
ll T,n,k;
class Mat{
public:
ll a[N][N];
inline ll* operator[](ll x){return a[x];}
inline void one(){_for(i,1,n)a[i][i]=1;return;}
inline void zero(){memset(a,0,sizeof(a));return;}
inline Mat operator*(Mat ma){
Mat ans;ans.zero();
_for(i,1,n){
_for(j,1,n){
ans[i][j]=0;
_for(k,1,n)ans[i][j]=(ans[i][j]+a[i][k]*ma[k][j]%P)%P;
}
}
return ans;
}
}a;
namespace SOLVE{
inline ll rnt(){
ll x=0,w=1;char c=getchar();
while(!isdigit(c)){if(c=='-')w=-1;c=getchar();}
while(isdigit(c))x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*w;
}
inline Mat fpow(Mat ma,ll b){
Mat ans;ans.zero();ans.one();
while(b){
if(b&1)ans=ans*ma;
ma=ma*ma,b>>=1;
}
return ans;
}
inline ll GetAnswer(Mat ma){
ll num=0;
_for(i,1,n)num=(num+ma[i][i]);
return num%P;
}
inline void In(){
n=rnt(),k=rnt();
a.zero();
_for(i,1,n)_for(j,1,n)a[i][j]=rnt();
Mat ans=fpow(a,k);
printf("%lld\n",GetAnswer(ans));
return;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号