树链剖分-重链剖分
树链剖分-重链剖分
前置知识
树形结构,链式前向星,线段树,DFS序,LCA。
定义
树链剖分(树剖):将树分解为一条条不相交的,从祖先到孙子的链。
第零部分:建树与基本概念
建树:给定\(n\)个节点用链式前向星(或邻接表)建树。
基本概念:
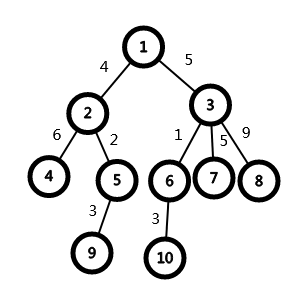
- 重儿子:假设\(x\)有\(n\)个儿子节点,其中以\(i\)儿子节点的为根子树大小最大,\(i\)就是\(x\)的重儿子。
- 轻儿子:除重儿子外的所有儿子均为轻儿子。
以上图为例
\(1\)的重儿子为\(3\),轻儿子为\(2\),
\(3\)的重儿子为\(6\),其余的为轻儿子。 - 轻边:\(x\)与轻儿子相连的边。
- 重边:\(x\)与重儿子相连的边。
- 轻链:均由轻儿子构成的一条链。
- 重链:均由重儿子构成的一条链。
第一部分:对表示节点信息的数组进行预处理
定义以下数组:
- \(d[x]\) 表示节点\(x\)的深度
- \(fa[x]\) 表示节点\(x\)的父亲节点
- \(son[x]\) 表示节点\(x\)的重儿子
- \(siz[x]\) 表示以节点\(x\)为根的子树大小
- \(top[x]\) 表示节点\(x\)所在重链的顶点
第一次DFS
数组\(d\)、\(fa\)、\(son\)均可用DFS很方便的求出,而\(siz\)数组则用到了DFS序的思想(详见《算法竞赛进阶指南》第\(0x21\)节)
void DFS1(int now,int dad)//now 为当前节点编号,dad 为其父节点编号
{
fa[now] = dad;//记录父节点
siz[now] = 1;//子树应算上根节点now
d[now] = d[dad] + 1;
for(int i = head[now]; i; i = edge[i].Next)
{
if(edge[i].to == dad)//对树进行dfs,故不访问父节点
continue;
DFS1(edge[i].to, now);
siz[son] += siz[edge[i].to];
//以一个节点为根的树(子树)的大小
//就是所有以其儿子节点为根的子树的大小之和+1
if(siz[son[now]] < siz[edge[i].to])
son[now] = edge[i].io;//更新重儿子
}
}
第二次DFS
现在还剩下\(top\)数组没有求,第二次DFS的目的便是将其求出。
- 对于一个节点的重儿子而言
这个重儿子节点肯定在一条重链上,该链的顶点必定是其祖宗 - 对于一个节点的轻儿子而言
这个轻儿子节点所在重链的顶点便是其本身(即新剖一条链),因为其父节点所在重链中其父节点的后继便是其父节点的重儿子,而非轻儿子
为了记录一个节点的重儿子对应的\(top\)值,故必须记录该重儿子所在链的顶点。
void DFS2(int now,int Top)
{
//Top即上文提到的重儿子所在链的顶点,因此now也就是其父节点的重儿子
//或者是以一个节点的轻儿子为顶点的链,now便是该节点,Top也是
top[now] = Top;
if(son[now])//叶节点没有儿子
DFS2(son[now], Top);//继续链接重链
else
return;//now是叶节点
for(int i = head[now]; i; i = edge[i].Next)//处理轻儿子
{
if(edge[i].to != fa[now] && edge[i].to != son[now])//轻儿子肯定不是父亲,也不是重儿子
DFS2(edge.[i].to, edge[i].to);//新剖一条以该轻儿子为顶点的链
}
}
以上便是树剖的基本内容,一切树剖的基础
第二部分:树剖求解LCA问题
类似于树上倍增法。
- 因为一棵树已经剖成了一条条互不相交的链,所以当两个节点\(x\)与\(y\)处在同一条链上时,\(LCA(x,y)\)就是\(x\)与\(y\)中深度最小者。
- 由节点\(x\)的祖先组成的链必定与由节点\(y\)的祖先组成的链相交于点\(LCA(x,y)\)
因此,我们可以将待求解\(LCA\)的两个节点通过\(fa\)数组一步一步上移,直到这两个节点处于同一条链上。
可以像树上倍增法那样先将两个节点调整到同一深度,再同时上移,也可每一次移动前寻找那个深度更大的点,将其上移,直到两个点处于同一条链上,此时\(LCA(x,y)\)就是\(x\)与\(y\)中深度最小者。
但这样做时间复杂度太大,因此可以进行一下优化:
- 思想: 既然目标是将\(x\)与\(y\)移到同一条链上,那么可以直接跳到该结点所在链的上一条链
- 做法: 找出所在链顶点深度较大节点,将该节点所在链的顶点的父节点的编号赋给该节点
这样做便实现了每次上移一条链,大大降低了时间复杂度。
void LCA(int x,int y)
{
while(top[x] != d[y])
{
if(d[top[x]] < d[top[y]])
swap(x,y);
x = fa[top[x]];
}
return d[x] < d[y] ? x : y ;
}
第三部分:最终挑战:线段树优化树上操作
第一部分分析:使用线段树进行优化的原因
- 你已经使用DFS1获取了\(d,fa,son,siz\)数组
- 接着,你又用DFS2获取了\(top\)数组
请分析DFS2遍历节点的顺序:
不难发现,总是先遍历重儿子,再遍历轻儿子。再想就可以发现总是在将已有重链遍历完后再遍历一条新链。
因此一条重链上的节点的遍历顺序是是连续的,并且完全可以将这条重链看成一个区间
众所周知,线段树是一种针对区间维护进行优化的数据结构。且码量和可读性都适中。
综上:对一棵剖完的树进行树上操作的最优优化方式是线段树
分析:在哪里使用线段树进行维护
区间
因为将一条重链看作一个区间的原因是其上节点的遍历顺序是连续的,所以在维护这个区间的时候要将节点的遍历顺序一起维护起来。
如下,上图是原来的(数据输入的)树,下图是对应地将遍历顺序维护的新树。

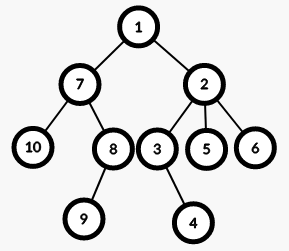
实现:使用线段树进行维护
建立区间
因为建立重链的是DFS2,所以建立区间要从DFS2入手。
因为建立由区间组成的新树的过程只改变了节点编号,因此建立新树只需重新记录节点编号。还会根据题目需要记录其他信息。
修改后的DFS2如下
void dfs2(int now,int Top)
{
top[now] = Top;
nw[++cntfordfs] = w[now];//w是题目需要记录的信息 cntfordfs是计数器
nid[now] = cntfordfs;//nid记录每个节点的新编号(或每个新节点的编号)
if(son[now])
dfs2(son[now], Top);
else
return;
for(int i = head[now]; i; i = Next[i])
{
if(to[i] != son[now] && to[i] != fa[now])
dfs2(to[i], to[i]);
}
}
使用线段树维护区间(以下以洛谷OJ P3384为例 )
题目传送门
题目已给出每个节点上都有一个值,那么\(w\)数组记录的就是该值。
线段树部分不做过多叙述,直接放代码
建树
struct SegmentTeee
{
int l,r,dat,add;
} t[N*4];
void bulid(int l,int r,int p)
{
t[p].l = l;
t[p].r = r;
if(l == r)
{
t[p].dat = nw[l];
return ;
}
int mid = (l + r) / 2;
bulid(l,mid,p*2);
bulid(mid+1,r,p*2+1);
t[p].dat = t[p*2].dat + t[p*2+1].dat;
}
懒标记/延迟修改
void spread(int p)
{
if(t[p].add)
{
t[p*2].dat += (t[p*2].r - t[p*2].l + 1)*t[p].add;
t[p*2+1].dat += (t[p*2+1].r - t[p*2+1].l + 1)*t[p].add;
t[p*2].add += t[p].add;
t[p*2+1].add += t[p].add;
}
t[p].add = 0;
}
区间修改
void change(int l,int r,int add,int p)
{
if(l <= t[p].l && t[p].r <= r)
{
t[p].add+=add;
t[p].dat+=(t[p].r - t[p].l + 1)*add;
return;
}
spread(p);
int mid=(t[p].l + t[p].r) / 2;
if(l <= mid)
change(l,r,add,p*2);
if(mid < r)
change(l,r,add,p*2+1);
t[p].dat = t[p*2].dat + t[p*2+1].dat;
}
区间求和
int ask(int l,int r,int p)
{
if(l <= t[p].l && t[p].r <= r)
return t[p].dat;
spread(p);
int sum=0;
int mid=(t[p].l + t[p].r)/2;
if(l <= mid)
sum += ask(l,r,p*2);
if(mid < r)
sum += ask(l,r,p*2+1);
return sum;
}
LCA处理树上最短路
题目中的操作主要分为两部分:树上最短路操作和子树操作。
两点之间的最短路,可以看成是从一个节点走到另一个节点,也可以看成是两个节点一起走,走到同一个节点(类似于数学中的相遇问题)。
这条路必然经过两个点的LCA,这是显而易见的。因此,两点间的最短路径就变成了两个点到它们的LCA的最短路径。
又因为上文提到的一条链构成一个连续的单调递增区间,所以题目中的最短路操作就被划分成了一个又一个连续的单调递增区间。
区间分两种情况(用\(x\)和\(y\)表示这两个点):
- \(x\)与\(y\)不在同一条链上
此时划分出的区间就是\(x\)到\(top[x]\)的最短路
while(top[x] != top[y])
{
if(d[top[x]] < d[top[y]])
swap(x,y);
//这里写操作
x = fa[top[x]];
}
- \(x\)与\(y\)在同一条链上
因为区间中元素是单调递增的,所以应先求出\(x\)与\(y\)中较浅者。此时区间就是较深者到较浅者的最短路
if(nid[x]>nid[y])
swap(x,y);
//这里写操作
结合一下
最短路修改
void LCAchange(int x,int y,int add)
{
while(top[x] != top[y])
{
if(d[top[x]] < d[top[y]])
swap(x,y);
change(nid[top[x]],nid[x],add,1);
x = fa[top[x]];
}
if(nid[x]>nid[y])
swap(x,y);
change(nid[x],nid[y],add,1);
}
最短路求和
int LCAask(int x,int y)
{
int sum = 0;
while(top[x] != top[y])
{
if(d[top[x]] < d[top[y]])
swap(x,y);
sum += ask(nid[top[x]],nid[x],1);
x = fa[top[x]];
}
if(nid[x]>nid[y])
swap(x,y);
sum += ask(nid[x],nid[y],1);
return sum;
}
子树操作转化为区间操作
由上文剖分重链的过程我们可以知道,一棵树上所有节点的dfs2遍历顺序(即\(nid\))可以构成一个单调递增区间。
因此对子树的操作也变成了对区间的操作。
假设一棵树,它的一颗子树根节点为\(x\),大小为\(size\),那么这棵树的dfs2遍历顺序构成的区间就是\(\{nid[x],nid[x]+1,···,nid[x]+siz-1\}\),
因此对这个子树的操作就可以写成对该区间的操作。
子树修改
void treechange(int x,int add)
{
change(nid[x],nid[x]+siz[x]-1,add,1);
}
子树求和
int treeask(int x)
{
return ask(nid[x],nid[x]+siz[x]-1,1);
}
完整代码
#include<bits/stdc++.h>
using namespace std;
#define N 100001
#define int long long
// 链式前向星
int to[N*2],head[N*2],Next[N*2];
int cntforedge=0;
void add(int fr,int t)
{
to[++cntforedge] = t;
Next[cntforedge] = head[fr];
head[fr] = cntforedge;
}
//树剖
int fa[N],siz[N],d[N],son[N];
void dfs1(int now,int dad)
{
fa[now] = dad;
d[now] = d[dad] + 1;
siz[now] = 1;
for(int i = head[now]; i; i = Next[i])
{
if(to[i] == dad)
continue;
dfs1(to[i], now);
siz[now] += siz[to[i]];
if(siz[son[now]] < siz[to[i]] && to[i] != dad)
son[now] = to[i];
}
}
int w[N],nw[N],nid[N],top[N];
int cntfordfs = 0;
void dfs2(int now,int Top)
{
top[now] = Top;
nw[++cntfordfs] = w[now];
nid[now] = cntfordfs;
if(son[now])
dfs2(son[now], Top);
else
return;
for(int i = head[now]; i; i = Next[i])
{
if(to[i] != son[now] && to[i] != fa[now])
dfs2(to[i], to[i]);
}
}
// 线段树
struct SegmentTeee
{
int l,r,dat,add;
} t[N*4];
void bulid(int l,int r,int p)
{
t[p].l = l;
t[p].r = r;
if(l == r)
{
t[p].dat = nw[l];
return ;
}
int mid = (l + r) / 2;
bulid(l,mid,p*2);
bulid(mid+1,r,p*2+1);
t[p].dat = t[p*2].dat + t[p*2+1].dat;
}
void spread(int p)
{
if(t[p].add)
{
t[p*2].dat += (t[p*2].r - t[p*2].l + 1)*t[p].add;
t[p*2+1].dat += (t[p*2+1].r - t[p*2+1].l + 1)*t[p].add;
t[p*2].add += t[p].add;
t[p*2+1].add += t[p].add;
}
t[p].add = 0;
}
void change(int l,int r,int add,int p)
{
if(l <= t[p].l && t[p].r <= r)
{
t[p].add+=add;
t[p].dat+=(t[p].r - t[p].l + 1)*add;
return;
}
spread(p);
int mid=(t[p].l + t[p].r) / 2;
if(l <= mid)
change(l,r,add,p*2);
if(mid < r)
change(l,r,add,p*2+1);
t[p].dat = t[p*2].dat + t[p*2+1].dat;
}
int ask(int l,int r,int p)
{
if(l <= t[p].l && t[p].r <= r)
return t[p].dat;
spread(p);
int sum=0;
int mid=(t[p].l + t[p].r)/2;
if(l <= mid)
sum += ask(l,r,p*2);
if(mid < r)
sum += ask(l,r,p*2+1);
return sum;
}
//树上操作->最短路
void LCAchange(int x,int y,int add)
{
while(top[x] != top[y])
{
if(d[top[x]] < d[top[y]])
swap(x,y);
change(nid[top[x]],nid[x],add,1);
x = fa[top[x]];
}
if(nid[x]>nid[y])
swap(x,y);
change(nid[x],nid[y],add,1);
}
int LCAask(int x,int y)
{
int sum = 0;
while(top[x] != top[y])
{
if(d[top[x]] < d[top[y]])
swap(x,y);
sum += ask(nid[top[x]],nid[x],1);
x = fa[top[x]];
}
if(nid[x]>nid[y])
swap(x,y);
sum += ask(nid[x],nid[y],1);
return sum;
}
// 树上操作->子树
void treechange(int x,int add)
{
change(nid[x],nid[x]+siz[x]-1,add,1);
}
int treeask(int x)
{
return ask(nid[x],nid[x]+siz[x]-1,1);
}
signed main()
{
int n,m,r,p;
cin >> n >> m >> r >> p;
for(int i = 1; i <= n; i++)
cin >> w[i];
for(int i = 1,f,t; i < n; i++)
{
cin>>f>>t;
add(f,t);
add(t,f);
}
dfs1(r,0);
dfs2(r,r);
bulid(1,n,1);
for(int i = 1,op,x,y,z; i <= m; i++)
{
cin >> op;
if(op == 1)
{
cin>>x>>y>>z;
LCAchange(x,y,z);
} else
if(op == 2)
{
cin>>x>>y;
cout<<LCAask(x,y)%p<<endl;
} else
if(op == 3)
{
cin>>x>>z;
treechange(x,z);
} else
if(op == 4)
{
cin>>x;
cout<<treeask(x)%p<<endl;
}
}
}

 树链剖分——重链剖分,我学的第一个蓝色算法
树链剖分——重链剖分,我学的第一个蓝色算法

 浙公网安备 33010602011771号
浙公网安备 33010602011771号