【总结】manacher

嗯嗯，\(manacher\) 是一种 \(O(n)\) 求解有关回文串问题的一个算法。

算法流程

首先，一个回文串最显著的特征是什么，或者说这个回文串的哪一个点最容易描述这个回文串。

显而易见，这个点是这个回文串的中心点。

接下来让我们以 \(abcddcbdbc\) 这个回文串为例子，介绍 \(manacher\)。

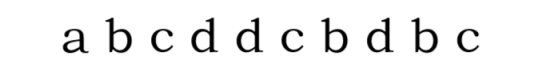
首先，回文串有奇有偶，但偶回文中心没有名确的回文中心，所以为保证统一，我们将回文串的每一个字符的左右放一个 '&' 符号。

这样的话，以每一个坐标 \(i\) 向左右扩展出的回文串就是奇数个数的了，不懂？感性理解一下。

考虑到点 \(i\) 是，我们首先是从头开始扩展的，十分可见这种算法的复杂度是不能被我们接受的，为什莫呢，思考一下每次都要扩展接近 \(\frac{n}{2}\) 次，这样的复杂度是 \(O(n^2)\)。

思考如何优化才能更优，首先我们不能从头开始扩展。

那我们设当前（\(1\dots i-1\) 之中）将左端点扩展到最远的点是 \(mid\)，\(mid\) 点最远将左端点扩展到了 \(r\)。

那让我们先考虑一下，在 \(i\le r\) 的时候，首先我们知道回文串是按中心点左右对称的，而 \(i\le r\) 所以 \(i\) 在 \(mid\) 的右侧必定会有一个 \(i'\) 它的情况会与 \(i\) 基本一致，所以 我们或许可以将 \(i\) 向左右扩展的初始值 \(d_i\) 设为 \(d_{i'}\)。

我在写这篇博客之前，一直没有搞懂一个问题，而大部分的博客中也没有讲述这个问题，现在我终于搞懂了这个问题，于是我打算将其记下来，希望能帮助你。

在 \(d_{i'}\) 大于 \(r-i+1\) 时，是需要将 \(d_i\) 的初始值设为 \(r-i+1\) 的，大部分博客没有说为什莫，只是一昧的写d[i]=min(d[i'],r-i+1)，我认为这是不友好的，因为这个语句至少对我来说是晦涩的，因为之前没有提到过，现在我来说一下为什莫这莫写。

在 \(d_{i'}\) 大于 \(r-i+1\) 时，是需要将 \(d_i\) 的初始值设为 \(r-i+1\) 的，因为 \(d_{i'}\) 的半径范围已经超过了当前回文过来的相同长度，也就是说，超过 \(r-i+1\) 的这部分可能会与 \(i\) 的情况不同。

如果 \(i>r\) 直接从 \(d_i=1\) 从头暴力扩展。

之后就是暴力扩展。

就是记得若 \(i+d_i-1\) 超过了 \(r\)，也就是说新一代的最远左端点出现了，记得更新 \(mid\) 和 \(r\)。

最后说一下 \(i\) 关于 \(mid\) 的对称点如何计算，\(i'=mid\times 2-i\)，感性理解即可。

最后笔者现默一下 \(manacher\)。

呃呃呃，还是别了。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 11000002;
char s[N], c[N << 1];
ll n = 0;
ll d[N << 1];
ll ans = 0;
int main() {
    cin >> s;
    c[n] = '#';
    c[++n] = '&';

    ll k = strlen(s);
    for (ll i = 1; i <= k; i++) {
        c[++n] = s[i - 1];
        c[++n] = '&';
    }
    c[n + 1] = '&';
    ll r = 0, mid = 1;
    for (ll i = 1; i <= n; i++) {
        if (r >= i)
            d[i] = min(d[mid * 2 - i], r - i + 1);
        else
            d[i] = 1;
        while (c[i - d[i]] == c[i + d[i]]) ++d[i];
        // if(c[i]=='&')
        ans = max(ans, (d[i] * 2 - 1) / 2);
        // else
        if (i + d[i] - 1 > r) {
            r = i + d[i] - 1;
            mid = i;
        }
    }
    cout << ans << "\n";
    return 0;
}

对于 P3805 这道板子题，我感觉需要说几点。

1. 不要用 \(stirng\)，因为 \(string\) 的空间是有限的，这么大似乎会爆。

2. 用一个变量将 \(strlen(s)\) 存下，不要在 \(for\) 内 \(strlne\)，这样会 \(TLE\)（复杂度很玄学了）。

\(\huge{Good}\) \(\huge{Bye。}\)