【总结】欧拉函数

更新公告

• 2025.8.7 重新编写本文。

显然，本文的一切都是关于它——\(\varphi\)。

前提

互质

若有正整数 \(a,b\) 且满足 \(\gcd(a,b)=1\)，则称 \(a,b\) 互质。

对于多种数的情况，我们把 \(\gcd(a,b,c)=1\) 的情况称为 \(a,b,c\) 互质。把 \(\gcd(a,b)=\gcd(a,c)=\gcd(b,c)=1\) 称为 \(a,b,c\) 两两互质。后者明显是一个更强的条件。

积性函数

如果 \(a,b\) 互质，有 \(f(a)\times f(b)=f(a\times b)\)，则称函数 \(f\) 为积性函数。

积性函数性质

易证，若函数 \(f\) 为积性函数，且在算法基础定理中 \(n= {\textstyle \prod_{i=1}^{m}} p_{i}^{c_i}\)，则 \(f(n)={\textstyle \prod_{i=1}^{m} }f(p_{i}^{c_i})\)。

正题·欧拉函数

含义

\(1\) 到 \(N\) 中所有与 \(N\) 互质的数的个数称为欧拉函数，记为 \(\varphi(N)\)。

性质

欧拉函数性质一：

\(N\) 可以表示为 \(p_{1}^{c_1}p_{2}^{c_2}p_{3}^{c_3}\dots p_{m}^{c_m}\)。

对于 \(N\) 的质因子 \(a\)，\(a\) 的倍数中在 \([1,N]\) 区间内的有 \(a,2a,3a,\dots,(N/a)*a\)，共有 \(N/a\) 个。

对于另一个 \(N\) 的质因子 \(b\),同理，\(b\) 的倍数中在 \([1,N]\) 区间内的有 \(N/b\) 个。

则在 \(1~N\) 中既不是 \(a\) 的倍数又不是 \(b\) 的倍数的个数按理说有 \(N-\frac{N}{a}-\frac{N}{b}\) 个，但 \(b\times a\) 的倍数被减了两次需要加回一次，所以个数是 \(N-\frac{N}{a}-\frac{N}{b}+\frac{N}{b\times a}=N\times (1-\frac{1}{a}-\frac{1}{b}+\frac{1}{a\times b})=n(1-\frac{1}{a})(1-\frac{1}{b})\)。

加以扩深的：\(\varphi(N)=N\times \prod_{p\mid N,p\in prime}{} (1-\frac{1}{p})\)

所以求欧拉函数的方法一：质因数分解法

int phi(int n){
	int ans=n;
	for(int i=2;i<=sqrt(n);i++){
		if(n%i==0){
			ans=ans/i*(i-1);
			while(n%i==0)n/=i;
		} 
	}
	if(n>1)ans=ans/n*(n-1);
	return ans; 
}

欧拉函数性质二：

\(\forall n>1\)，\(1\) 到 \(n\) 中与 \(n\) 互质的数的和为 \(\frac{n\times \varphi(n)}{2}\)。

\(\because gcd(n,x)=gcd(n,n-x)\)

\(\therefore\) 与 \(n\) 互质的数 \(x,n-x\) 成对出现，平均值为 \(\frac{n}{2}\)。

因此，与 \(n\) 互质的数的平均值是 \(\frac{n}{2}\)，由此推出性质二。

欧拉函数性质三：

对 \(a,b\) 质因数分解，可直接得出 \(\varphi(a)\times \varphi(b)=\varphi(a\times b)\)，这就是前提中的积性函数。

欧拉函数性质四：

设 \(p\) 为质数，若 \(p\mid n,p^2\mid n\)，则\(\varphi (n)=\varphi(n/p)\times p\)。

证：由 \(p\mid n,p^2\mid n\)，则 \(n,n/p\) 具有相同质因子。

所以：

\[\varphi(n)=n\times \prod_{p_1\mid n,p_1\in prime} (1-\frac{1}{p_1}) \]

\[\varphi(\frac{n}{p})=\frac{n}{p}\times \prod_{p_1\mid n,p_1\in prime}(1-\frac{1}{p_1}) \]

于是 \(\varphi(\frac{n}{p})\times p=\varphi(n)\)。

欧拉函数性质五：

设 \(p\) 为质数，若 \(p\mid n,p^2 \nmid n\)，则\(\varphi (n)=\varphi(n/p)\times (p-1)\)。

由 \(p\mid n,p^2\nmid n\)，则 \(\frac{n}{p}\) 与 \(n\) 相比缺少了 \(p\) 这个质因子。

所以：

\[\varphi(n)=n\times \prod_{p_1\mid n,p_1\in prime} (1-\frac{1}{p_1}) \]

\[\varphi(\frac{n}{p})=\frac{n}{p}\times \prod_{p_1\mid \frac{n}{p},p_1\in prime}(1-\frac{1}{p_1}) \]

然而 \(\frac{n}{p}\) 与 \(n\) 之间就只差了 \(p\) 一个约数。

所以：

\[\varphi(\frac{n}{p})\times p\times (1-\frac{1}{p})= \varphi(n) \]

则：

\[\varphi(\frac{n}{p})\times(p-1)= \varphi(n) \]

根据性质四和性质五，我们可以得到一个大规模 \(O(n)\) 处理出 \(1\cdots n\)
所有数的函数值的算法。

即在线性筛（也可以是埃式筛）中在筛质数的同时，将函数值处理出来。

void get_phi(ll n){
    phi[1]=1;
    for(ll i=1;i<=n;i++){
        if(vis[i]==0){
            vis[i]=i;
            phi[i]=i-1;
            primes[++cnt]=i;
        }
        for(ll j=1;j<=cnt;j++){
            if(primes[j]>n/i||vis[i]<primes[j])break;
            if(i%primes[j]==0)phi[i*primes[j]]=phi[i]*primes[j];
            else phi[i*primes[j]]=phi[i]*(primes[j]-1);
            vis[i*primes[j]]=primes[j];
        }
    }
}

这个东东呢，是笔者现场默写的，争取率呢，笔者也不知道（雾。

欧拉函数性质六：

$ {\textstyle \sum_{d\mid n}} \varphi(d)=n$。

这个真不会。。。

2025.8.7 注：嗯嗯嗯，现在会了。

证明：

考虑令 \(f(n)=\sum_{d\mid n}\varphi(d)\)。

然后考虑 \(f(n)\times f(m)\) 的结果。

思考两个正整数 \(a,b\)。

将 \(a\) 的约数集合和 \(b\) 的约数集合中的数两两相乘。

举个例子：

\(a=54,b=32\)

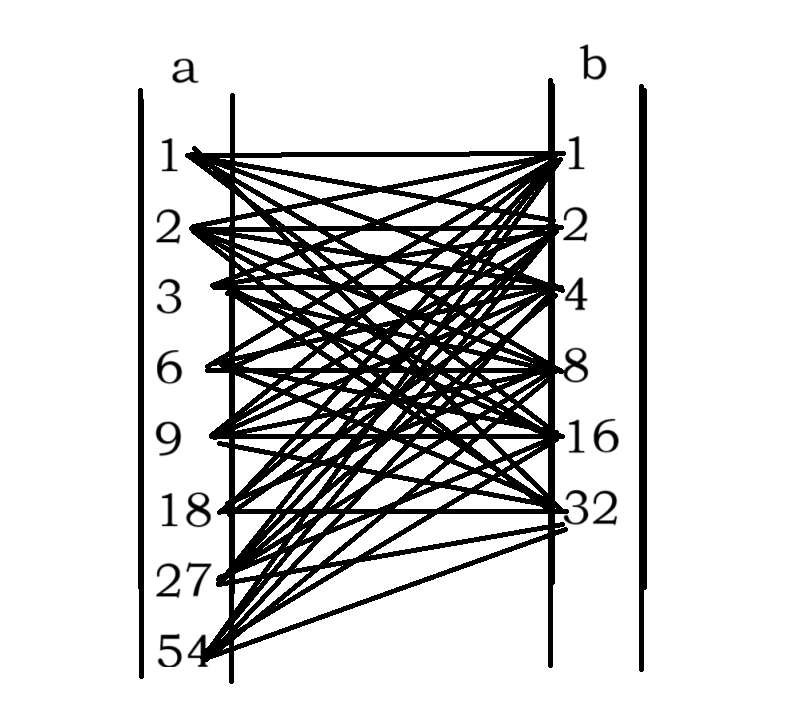
在这张图中，我们可以明了的看见，这两个约数集合相乘，组合出了 \(a\times b\) 的所有约数。

看回了原来的公式 \(f(n)\times f(m)\) 发现，这本质上是 \(n\) 的一约数的欧拉函数值与 \(m\) 一约数欧拉函数值得相乘，然而 \(\varphi\) 是积性函数，所以 \(f(n)\times f(m)=f(n\times m)\)。

所以 \(f(n)=\prod_{p\mid n,p\in prime}f(p)^c\)，明显对于质数 \(p\)，\(f(p)=p\)，所以 \(f(n)=n\)。

后续

积性函数还会涉及狄利克雷卷积、莫比乌斯反演等，但这些知识过于高贵，超过了作者脑子的思考范围，所以作者并不打算在这一文章中继续讲。

所以，之后会有一篇讲的。。